The Möbius Transformation
(Lecture 11 of Mathematical Methods II.)
The Möbius transform is a particular family of conformal mappings, given by:
\begin{equation}
\label{eq:TueFeb12135555CET2013}
w=\frac{az+b}{cz+d}
\end{equation}
with $a$, $b$, $c$ and $d\in\mathbf{C}$ such that $ad\neq bc$. It maps lines and circles into other lines and circles, since:
\begin{equation}
\label{eq:TueFeb12150253CET2013}
w=\frac{az+b}{cz+d}=\frac{a}{c}+\frac{bc-ad}{c}\frac{1}{cz+d}
\end{equation}
is a combination of linear transform $z_1=cz+d$ followed by an inverse $z_2=1/z_1$ then a scaling by $(bc-ad)/c$ and finally transation by $a/c$, each of which in isolation preserves circles.
Geometrically, a Möbius transformation corresponds to mapping the plane onto a sphere (a type of projection known as stereographic to which we will come back later in the course), rotating and moving the sphere to a new location and orientation in its own, 3D space, and then performing back the inverse stereographic projection (from the new position of the sphere) to the plane. The following movie shows these operations in a transparent way:
There exists a unique Möbius transformation that maps three distinct points $z_i$, $i\in\{1,2,3\}$, onto three distinct points $w_i$, respectively. An implicit formula for the mapping is given by the equation:
\begin{equation}
\label{eq:TueFeb12152358CET2013}
\frac{(z-z_1)(z_2-z_3)}{(z-z_3)(z_2-z_1)}
=\frac{(w-w_1)(w_2-w_3)}{(w-w_3)(w_2-w_1)}\,.
\end{equation}
For example, the Möbius transform that maps $\{-i,1,i\}$ into $\{-1,0,1\}$ leads to ${(z+i)(1-i)}{(z-i)(1+i)}/({w+1}{-w+1})=i(1-z)/(1+z)$ It is plotted below:
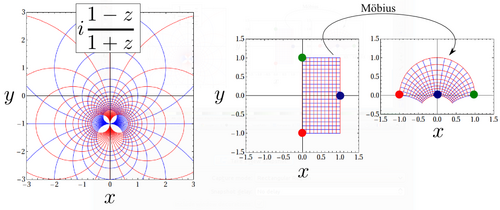
One point can be sent to infinity (through the inversion of the plane, $1/z$), which, by bijection, implies that $\infty$ is also sent to a finite point of $\mathbf{C}$. Back to the sphere representation, this special point is the north pole, from where the other points are projected. This affords a compactification of the complex numbers.
