Complex functions of complex numbers
(Lecture 2 of Mathematical Methods II.)
When we study the action of complex algebra not on a single number but on the entire complex plane as a whole, we start to study analysis, that is, the algebra of functions and their global properties.
The general case is that of a complex-valued function $w(z)=u(z)+iv(z)$ taking complex arguments $z=x+iy$. In this way, $u$ and $v$ can also be seen as real-valued functions of two real-variables $u(x,y)+iv(x,y)$.
Let us assume again the operation $z\rightarrow z^2$, now understood as a function, $w$, which means that we are not interested in squaring a given number (like $i$) but on the properties related to all complex numbers under the action of $w$.
In this case, $w(x+iy)=x^2-y^2+2ixy$ and, obviously, $u(x,y)=x^2-y^2$ while $v(x,y)=2xy$.
The representation of the square function is simple enough in real analysis, as it fits in a 2D space. In complex analysis, we are dealing with 2 (argument)$\times$2 (value) = 4D space, which is notoriously difficult to picture.
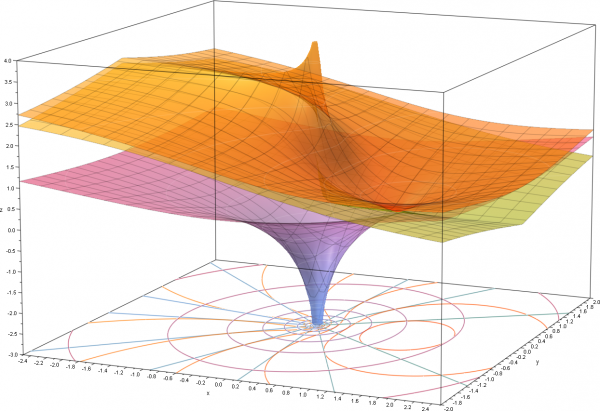
While there are a lot of different ways to represent such complex-valued functions of a complex variables, such as 3D plots of $u$ and $v$ separately, of the modulus of the function, domain coloring~[1], etc., an insightful visualization is provided by the so-called W-space (or UV-plane) representation. It consists in mapping each point in the original (argument) plane to one or various points in the destination (function) plane.
For instance, vertical lines, with equations $x=c$ ($c$ variable) map into $u=c^2-y^2$ and $v=2cy$, that is, since in this case we can express $u$ as a function of $v$ as $u=c^2-v^2/(4c^2)$, as parabolas of varying curvatures and pointing to the right. Horizontal lines point to the opposite direction. This seems a natural transformation for the square function, that can be represented as follow:
The polar representation can be used to query the transformation of circles: $re^{i\theta}\rightarrow r^2e^{2i\theta}$. Here we see that a circle maps to another circle. The upper half circle maps to a full circle, so that a full circle overlaps twice with itself. This is also the reason why twelve lines on the left are mapped to six only on the right.
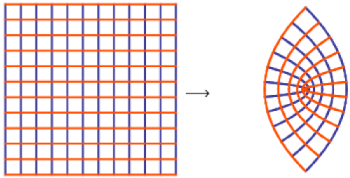
A characteristic feature of such complex mapping is that they are conformal, i.e., they preserve locally angles between curves. Sometimes, figures more recognizable than simple curves (grids, concentric circles, rays, etc.) are used, such as the face of a cat (Arnold's cat) or, with the computer power now available even more complex patterns. This shows the $z\rightarrow z^2$ conformal mapping of a richly decorated image~[2]:
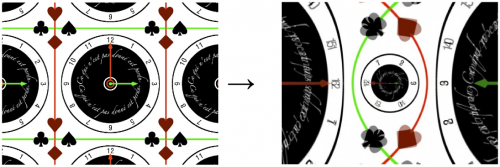
Again we see that the squaring results in overlap. This becomes an issue if we want to address the reverse problem of mapping back the W-space to the original (Z) one, or, equivalently, map the reverse function, which in the case of squaring is, of course, $w(z)=\sqrt{x+iy}=\sqrt{r}e^{i\theta/2}$. Each point $x+iy$ in the Z space map to two points that are opposite to each other in the W plane (the exact mapping in Cartesian coordinates is:
$$\sqrt{z}=\pm\left(\sqrt{\frac{\sqrt{x^2 + y^2}+x}{2}}+i\mathrm{s}(y)\sqrt{\frac{\sqrt{x^2 + y^2}-x}{2}}\right)$$
with $\mathrm{s}(y)=\frac{y}{|y|}$ if $y\neq0$ and 0 otherwise.) Such functions are called multi-valued.
While this seems a rather secondary detail, that moreover is already known from real calculus (where the square root of $x$ could also be a two-valued $\pm\sqrt{x}$ function), the "connectedness" of the complex plane—a notion we will explore furthermore in the next lecture—makes it an important and sui generi aspect of complex geometry.
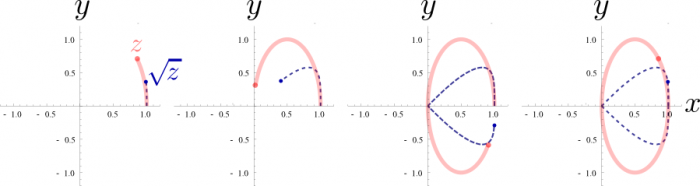
For instance, consider, indeed, the mapping of the unit circle by the square root function:
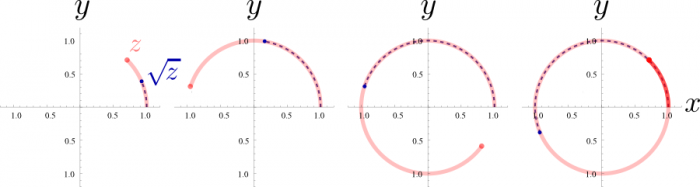
The argument $z$, in light red, starts at $z_0=1$, where clearly the function $\sqrt{z_0}$, in dashed blue, equals 1 also, so the two trajectories start together. Since $\sqrt{e^{i\theta}}=e^{i\theta/2}$, the function lacks behind the argument, as we can see in the first panel where we take the first shot of the function. Everything looks fine up to panel three, but in the fourth panel, one can see the problem of the complex version of $(\pm\sqrt{x})^2=x$: while we have continuously circled around and looped back to our starting point, the function did not complete the loop but was left in mid-course at minus the position it took when we first visited the first point. There never was anything to prevent us from changing the definition or choice of the function, or any indication this was happening, whereas in the real plane, one cannot connect to the opposite sign solution.
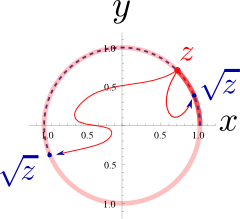
This ambiguity in the value of the function is troublesome, since $f(z)=\sqrt{z}$ can become $f(z)=-\sqrt{z}$ as we follow the function on a smooth, continuous trajectory. We can expect troubles with elementary algebra if $f(z)=-f(z)$ for nonzero objects.
Note that there is no real inconsistency as we can keep the ambiguity under control by keeping trace of the phase and remembering to accumulate $2\pi$ factor once we circled round: calling $z_0$ and $z_1$ the same point in the complex plane but with zero or one completion of the circle: $\sqrt{z_1}=\sqrt{e^{i(2\pi+\theta)}}=e^{i(2\pi+\theta)/2}={e^{i\pi}e^{i\theta/2}}=-e^{i\theta/2}=-\sqrt{z_0}$. The problem can thus be traced to the fact that the phase in the space is defined modulo $2\pi$. Another typical problem of the phase is that it is undefined at the origin. We say that it is singular here. These are the source of multi-valuedness problems of complex numbers and their origin, the phase singularity, is called a "branch point". A well-behaved, single-valued function can be restored if we do not circle the branch point and thus do not allow to build up the phase. Consider for instance the modified loop which grazes (and passes by) zero but does not circle it in. In this case, the square root returns to its point of origin with the argument.
This can be ensured by opening a "branch cut" in the complex plane, for instance half the real-line, $]-\infty;0[$. This is the complex version of adopting a definition for the function, which is called the principal value. The mapping of the principal value of the square root looks as follows:
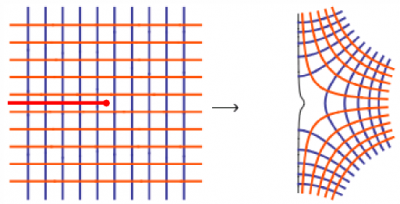
Typically, the whole complex space as the domain of the function is mapped to part of it only as the image of the function. For the square root, this effectively halves the W-space. The blue lines that "try" to cross the cut (notice the branch cut in red), i.e., $x=c$ with $c$ a negative constant, are torn apart in the $W$ space. Plotting the real and imaginary parts of the function therefore leads to a clear manifestation of the branch cut: this is the line where an otherwise continuous function becomes discontinuous.
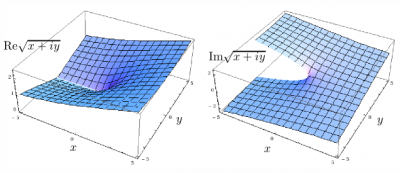
Note that this is rather artificial as this depends on one's definition of the function, whether defining $\sqrt{z}$ as the multi-valued $\sqrt{r}e^{i\theta/2}$ or as a principal value, which could be along any branch cut.
A better and more elegant approach is to see the branch cut not as a barrier that stops the function in its course, but as a passage into another space, which allows the function to remain single-valued, by providing as many copies as the complex plane as necessary to lift the overlaps. The enlarged complex plane that results is function specific, and is called the Riemann surface of the function. The Riemann surface for the square root is shown below:
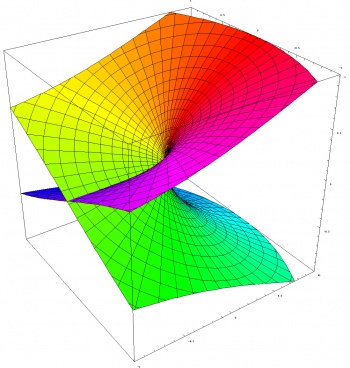
The origin of the plane is (aptly) at the center of the graph. The branch cut is where the two sheets intersect. Starting in the reddish region and circling around the branch point, we continuously pass from the upper sheet to the lower one and arrive in the greenish region where the function takes the value $-\sqrt{z}$, this time with no ambiguity as the argument is a different point (on the lower sheet). Continuing the circling we cross the branch cut again and, after two revolutions on the Riemann surface, come back to our initial point on the upper sheet as the function also complete its (only one) revolution in its W-space.
Other functions have different Riemann surfaces. The $n$-th root has $n$ sheets (for integer $n$). Such features that appear to be technical annoyances turn out to be central features of the fabric of complex numbers, which we will see in later lectures to be connected to some of their most powerful properties.
Another important multi-valued function is the logarithm, which, let us remind, is for a number $z$ the number $w$ such that $e^w=z$. The polar description of $z=re^{i\theta}$ sees $w$ simply defined as $\log(z)=\log(r)+i\theta$. This shows that the logarithm is defined for all $z\neq0$. Note the intimate connection between the logarithm and the phase (as already commented, phases of complex numbers add-up in their multiplication, which is the characteristic behaviour of a logarithm). The multi-valuedness problem is here due to the fact that a phase is defined modulo $2\pi$. The conformal mapping of circles centered around the origin in the U-space are vertical lines $(u,v)=(\log(r),\theta)$ in the W-space and the Riemann surface is therefore a never ending staircase that ones keeps climbing up as the phase drifts forever.
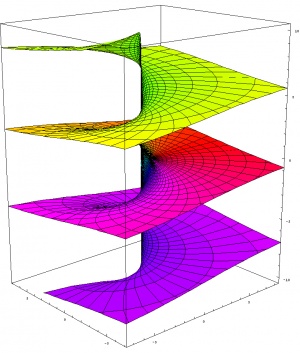
Let us remember that this complex structure, already quite difficult to picture, is merely the support of the function itself. We conclude this lecture with the display of a combination of only but a few popular representations for the function itself. Now that we have discussed complex functions and approached the way to represent them, in the rest of the course, we will address the deeper problem of studying their mathematical properties.