Limits and continuity (for the physicist)
(Lecture 4 of Mathematical Methods II.)
We have seen in the previous lecture how a function like $\sqrt{z}$ appeared to display features of discontinuity at the branch cut which were not intrinsic to the function itself (since it appears to be continuous on its Riemann surface). The branch cut is a global property of the function while continuity is a local one. Locality is an important concept in physics. It was a driving one for Einstein. Locally to a point, the first terms of an expansion are enough to describe a function, or, said colloquially: locally, things are linear, and therefore, easy. It is only when one wants to describe the distant (or global) behavior that more, or all terms are required. We will explore today concepts of neighborhoods and particularly of the property of continuity in them.
The idea of continuity is formalized by stating that when the variable approaches a point, say, $z_0$, the function of the variable approaches the value of the function at this point. To make this precise, we need to introduce the concept of a limit.
Definition: $f$ has the limit $w_0$ as $z\rightarrow z_0$ provided that the value $f(z)$ can be made as close as required to the value $w_0$ by taking $z$ to be sufficiently close to $z_0$. We write:
\begin{equation}
\lim_{z\rightarrow z_0}f(z)=w_0\,.
\end{equation}
This is formally spelled out through the so-called "Weierstrass $\epsilon-\delta$" formulation:
\begin{equation}
(\forall\epsilon>0)(\exists\delta>0)(|z-z_0|<\delta\Rightarrow|f(z)-w_0|<\epsilon)\,.
\end{equation}
Once we have this concept at hand, continuity follows straightforwardly: a function is continuous at the point $z_0$ if its limit when $z$ approaches $z_0$ is $f(z_0)$. The accurate definition that covers for all eventualities reads as follows:
Definition: The complex function $f$ is continuous at $z_0$ iff:
- $f(z_0)$ exists.
- $\displaystyle\lim_{z\rightarrow z_0}f(z)$ exists.
- $\displaystyle\lim_{z\rightarrow z_0}f(z)=f(z_0)$.
Here we have defined continuity as a local concept (at a point). A function is continuous if it is continuous at all points.
This is the conceptual foundation. We know explore some of the consequences brought by the complex geometry.
In the $U$-$V$ representation of $f(x+iy)=u(x,y)+iv(x,y)$, for the real function $u$ (resp.~$v$), for which continuity reads:
$$\lim_{(x,y)\rightarrow(x_0,y_0)}u(x,y)=u_0$$
iff
\begin{equation}
(\forall\epsilon>0)(\exists\delta>0)(\sqrt{(x-x_0)^2+(y-y_0)^2}<\delta\Rightarrow|u(x,y)-u_0|<\epsilon)\,.
\end{equation}
we have:
\begin{equation} \lim_{z\rightarrow z_0}f(z)= w_0\qquad \Leftrightarrow\qquad \lim_{(x,y)\rightarrow(x_0,y_0)}u(x,y)=u_0\quad\mathrm{and}\quad\lim_{(x,y)\rightarrow(x_0,y_0)}v(x,y)=v_0\,, \end{equation}
for $w_0=u_0+iv_0$ and $z_0=x_0+iy_0$.
Crucially, the limit must not depend on the trajectory by which it is approached. For instance, if $U(x,y)=2x^3/(x^2+y^2)$, $\lim_{(x,y)\rightarrow(0,0)} U(x,y)=0$, while $U(x,y)=(xy)/(x^2+y^2)$ has no limit at the origin.
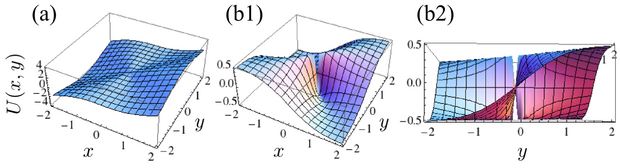
3D plots of $U(x,y)$ for (a) $U(x,y)=2x^3/(x^2+y^2)$ and (b) $U(x,y)=(xy)/(x^2+y^2)$. The former has a limit at zero, the latter not. As a consequence, it is not continuous there.
