Harmonic functions.
(Lecture 8 of Mathematical Methods II.)
We have seen that when a complex function $w(z)=u(x,y)+iv(x,y)$ is differentiable (holomorphic), its real and imaginary parts satisfy the Cauchy-Riemann equations:
\begin{align} \label{eq:CR} &\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y}\,,\\ &\frac{\partial u}{\partial y}=-\frac{\partial v}{\partial x}\,. \end{align}
This was not entirely unexpected. If the function is differentiable, surely this has repercussion on its real and imaginary parts. More surprising, however, is that the opposite also holds, namely if $u$ and $v$ are $\mathbf{R}$-differentiable and satisfy Eq.~\ref{eq:CR}, then $u+iv$ is $\mathbf{C}$-differentiable, that is, it is holomorphic and therefore, as we learned last time, also analytic. The mere conditions~\ref{eq:CR} ensure that derivatives to all orders exist (since one can differentiate indefinitely an analytic function). This is a considerably more stringent condition than in the case of the real variable.
From the theory of functions of several variables, we know that if $\partial u/\partial x$, $\partial u/\partial y$, but also
$$\frac{\partial}{\partial_x}\frac{\partial u}{\partial y}\quad\text{and}\quad\frac{\partial}{\partial_y}\frac{\partial u}{\partial x}$$
exist and are continuous, then:
$$\frac{\partial}{\partial x}\frac{\partial u}{\partial y}=\frac{\partial}{\partial y}\frac{\partial u}{\partial x}\,.$$
We will note such second order derivatives $\frac{\partial^2 u}{\partial x\partial y}$ (we have just seen that the order in the denominator does not matter).
If a function $w$ is holomorphic, it has derivatives to all order. Let us consider the Laplacian of its real part:
\begin{align} \nabla^2 u&=\frac{\partial^2u}{\partial x^2}+\frac{\partial^2u}{\partial y^2}\\ &=\frac{\partial}{\partial x}\frac{\partial v}{\partial y}-\frac{\partial}{\partial y}\frac{\partial v}{\partial x}=0 \end{align}
where we have used again the commutation of $\partial x$ and $\partial y$, which is satisfied for the real part of an holomorphic function, that also obeys, as we have just shown, Laplace equation $\nabla^2 u=0$. We would find just the same that also $\nabla^2 v=0$.
Laplace equation is a particular type of very important equations in physics, such as Poisson's equation $\nabla^2\varphi=f$ used in the Newtonian theory of gravity or electrostatic, Helmholtz's equation~$\nabla^2 w+k^2 w=0$ used in the study of wave propagation, the heat equation $\nabla^2T=\partial T/\partial t$, Schrödinger equation $\nabla^2\psi=-2i\partial\psi/\partial t$, in fluid dynamics where the laplacian of a velocity field combines with other factors, etc.
Solutions of the simplest case that is Laplace's equation are called harmonic functions. As simple as it looks, no general solution for Laplace's equation is yet known, only in the case of simple geometries (box, cylinder, sphere, etc.) Yet all of them share identical properties, as strong for the real variable than holomorphicity in the complex one (in fact Harmonic functions can be regarded as the counterparts in the real plane of holomorphic variables in the complex one).
The most important one is the so-called Gauss's harmonic function theorem, that for a real (or imaginary) part of an holomorphic function (that is, in 2D) reads:
If $u$ is harmonic in a connected region $G$ that contains an open ball $\mathcal{B}(z_0,r)$ for some $r$ then:
$$u(z_0)=\frac{1}{2\pi}\int_0^{2\pi}u(z_0+re^{i\theta})\,d\theta\,.$$
We will demonstrate this when we address the question of integrals in the complex plane. For now, replacing $2\pi\rightarrow2\pi r$ before the integral and $d\theta\rightarrow rd\theta$ below, we see that this property means that the average value of an harmonic function over a disk is equal to the value of the function at the center of the disk (regardless of the radius of the disk).
As a consequence, an harmonic function has no local maxima or minima (or, more precisely, if it has, it is constant).
A corollary is that if $f$ is harmonic in a bounded connected region, then its absolute maximum and minimum occur on the boundary.
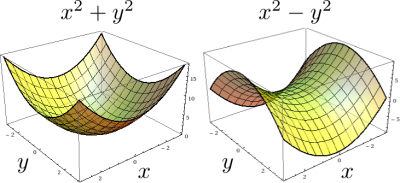
The function $x^2+y^2$ (left) is not harmonic since it has a local minimum, while the function $x^2-y^2$ (right), in the shape of a saddle, is.
Another corollary is that if $f$ and $g$ are harmonic functions such that $f=g$ on the boundary of the domain where they are defined, then $f=g$ also inside the entire region as well.
As a consequence, a solution to Laplace's equation is uniquely determined if:
- the value of the function is specified on all boundaries (Dirichlet boundary conditions), or
- the normal derivative of the function is specified on all boundaries (Neumann boundary conditions).
There exists a reciprocal to the fact that holomorphic functions have harmonic real and imaginary parts:
If $u$ is harmonic on a simply connected region $G$, then there exists a harmonic function $v$ such that $f = u + iv$ is holomorphic in $G$. The function $v$ is called the harmonic conjugate of $u$.
From this link between holomorphic and harmonic functions, we can show that harmonic functions are infinitely differentiable: assume that $u$ is harmonic, then for any $z=x+iy$, in an open ball centered on $z$ there exists $f$ holomorphic such that $f=u+iv$ (a ball is simply connected). Since $f$ is infinitely differentiable at $z$, so is its real part. Because $z$ was chosen arbitrarily, $u$ is differentiable everywhere.
We have seen properties of Harmonic functions. Let us discuss briefly how to actually solve Laplace's equation. Because it is linear, the superposition of any two solutions is also a solution. This allows to solve complicated problems by solving simpler problems that provide a basis for the general solutions.
In simple geometries, such as a square in Cartesian coordinates or a sphere in 3D, Laplace's equation can be solved by separation of variables, that is, writing $u(x,y)=X(x)Y(y)$ a product of two functions, that inserted into $\nabla^2 u=0$ yields:
$$\frac{1}{X}\frac{d^2X}{dx^2}=-\frac{1}{Y}\frac{d^2Y}{dy^2}\,.$$
As the functions that do not depend on each other's variable each figure on one side of the equation, there are both equal to one (and the same) constant $k$. The solution of the ordinary differential equation that follows yields the basis of solutions.
When the geometry does not allow such an approach, Laplacians can be easily computed by numerical methods, which are stable and accurate thanks to properties of harmonic functions. The Laplacian is indeed approximated as the local deviation of the function:
$$\nabla^2f \approx \frac{[f(x+h,y)+f(x-h,y)-2f(x,y)]+[f(x,y+h)+f(x,y-h)-2f(x,y)]}{h^2}$$
(note that $f(x+h,y)+f(x-h,y)-2f(x,y)=[f(x+h,y)-f(x,y)]+[f(x-h,y)-f(x,y)]$). Typically, the grid to compute such functions is not square, but is tessellated to improve numerical performances, an approach used in so-called finite element methods.
As a last note, given the property of the Laplacian operator to represent the deviation from the local average, instead of the notation $\nabla^2=\mathrm{div}\cdot\mathrm{grad}$ that we have used, it is common to write instead simply $\Delta$.
