The Cauchy-Goursat theorem and its integral forms
(Lecture 14 of Mathematical Methods II.)
We have introduced Cauchy's theorem through the complex Green theorem (we further assumed the real version of Green's theorem). As it is an extremely important piece of complex analysis, we will prove it again using a more direct approach that is also emblematic of the sort of reasoning that will bring us to other results of this lecture. This approach will also relax the hypothesis of continuous derivative, needed for the demonstration from the Green approach. In fact, this more general proof was established by Goursat on top of that of Cauchy, that it uses to eliminate particular cases, so that the equality $\oint f(z)\,dz=0$ for an holomorphic function on any path of a simply connected domain is often called the Cauchy-Goursat theorem.
We will prove it on a triangle ABC. The proof on a polygon follows by breaking it into sub-triangles; the proof on a simple closed path follows from approaching it by a polygon with many sides and the proof on not simply connected regions follow from cutting out simply connecting regions out of it.
For the triangle, as shown below, the proof proceed by iterations to smaller triangles, until the differentiability of $f$ can be invoked in the limit of small triangles. We take E, F and D the mid-points between AB, BC and CA respectively.
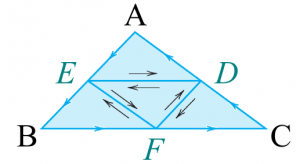
The contour integral is now splitted as follows:
\begin{align}
\oint_\Delta&=\oint_{ABCA}=\int_{DAE}+\int_{EBF}+\int_{FCD}\\
&=\left[\int_{DAE}+\int_{ED}-\int_{ED}\right]
+\left[\int_{EBF}+\int_{FE}-\int_{FE}\right]
+\left[\int_{FCD}+\int_{DF}-\int_{DF}\right]\\
&=\left[\int_{DAE}+\int_{ED}\right]
+\left[\int_{EBF}+\int_{FE}\right]
+\left[\int_{FCD}+\int_{DF}\right]
+\left\{\int_{DE}+\int_{EF}+\int_{FD}\right\}\\
&=\oint_{DAED}+\oint_{EBFE}+\oint_{FCDF}+\oint_{DEFD}\,.
\end{align}
In this way we have scaled down the problem from one triangle to four sub-triangles. The integral $\oint f(z)\,dz$ exists and is finite for any of these triangles. Of the four values that result, let us call $\Delta_1$ the sub-triangle that yields the largest value of the contour integrals. From the triangle inequality:
\begin{equation}
\left|\oint_\Delta f(z)\,dz\right|\le4\left|\oint_{\Delta_1}f(z)\,dz\right|\,.
\end{equation}
We can repeat the same procedure on the triangle~$\Delta_1$ and arrive to $\left|\oint_{\Delta_1}f(z)\,dz\right|\le4\left|\oint_{\Delta_2}f(z)\,dz\right|$ where $\Delta_2$ is a sub-triangle of $\Delta_1$ (the one that yields the largest contour integral). Calling $\Delta_n$ the $n$th order sub-triangle chosen in this way, we arrive to:
\begin{equation}
\label{eq:MonFeb25170120CET2013}
\left|\oint_\Delta f(z)\,dz\right|\le4^n\left|\oint_{\Delta_n}f(z)\,dz\right|\,.
\end{equation}
Note that each triangle halves its perimeter in such an iteration, so that if the initial perimeter (of $\Delta$) is $P$, the perimeter of $\Delta_n$ is $P/2^n$.
We now use the fact that $f$ is differentiable, that is, $f(z)=f(z_0)+f'(z_0)(z-z_0)+h(z)(z-z_0)$ where
\begin{equation}
h(z)=\frac{f(z)-f(z_0)}{z-z_0}-f'(z_0)
\end{equation}
is such that $\lim_{z\rightarrow z_0}h(z)=0$, that is, $\forall\epsilon>0$, $\exists\eta>0$ such that $|z-z_0|<\eta\Rightarrow|h(z)|<\epsilon$. For any $\epsilon>0$, let us then iterate the triangle division until $\Delta_n$ is included in the disk $|z-z_0|<\eta$ for all $z_0$ in $\Delta_n$.
For any point $z_0$ within the triangle $\Delta_n$ and any $z$ on the contour, we have $|z-z_0|< P/2^n$ (the distance from a point to the triangle is smaller than the perimeter). From $|\oint f(z)\,dz|\le ML$ ($M$ and $L$ being the max of $f$ and the length of the path of integration, respectively), we obtain:
\begin{equation}
\left|\oint_{\Delta_n}f(z)\,dz\right|=\left|\oint_{\Delta_n}h(z)(z-z_0)\,dz\right|\le\frac{\epsilon P}{2^n}\frac{P}{2^n}
\end{equation}
where we have cancelled $\oint dz$ and $f'(z_0)\oint(z-z_0)dz$ from Cauchy's theorem (assuming continuity of the derivative). This achieves to prove Cauchy-Goursat's theorem since from Eq.~\ref{eq:MonFeb25170120CET2013}, we have finally:
\begin{equation}
\left|\oint_\Delta f(z)\,dz\right|\le\epsilon P^2
\end{equation}
where~$\epsilon$ is as small as desired.
One can check where the demonstration breaks for a non-differentiable function.
Such powerful properties allow us to compute straightforwarly integrals of the form:
\begin{equation}
\oint_\mathcal{C}\frac{f(z)}{z-z_0}\,dz
\end{equation}
where $\mathcal{C}$ is a simple closed path in a simply connected domain~$D$ that encloses~$z_0$ and where $f$ is holomorphic. Indeed
\begin{equation}
\oint_\mathcal{C}\frac{f(z)}{z-z_0}\,dz=\oint_\mathcal{C}\frac{f(z)-f(z_0)}{z-z_0}\,dz+f(z_0)\oint_\mathcal{C}\frac{1}{z-z_0}\,dz
\end{equation}
where the second term is simply $2i\pi f(z_0)$ while the first term is shown to vanish as follows. First we deform the path of integration to a circle~$C$ centered on $z_0$ and of radius~$\rho$. The function $f$ being continuous (since it is differentiable by definition), then for any~$\epsilon>0$, there exists $\eta$ such that $|f(z)-f(z_0)|<\epsilon$ for all $z$ such that $|z-z_0|<\eta$. For the given $\epsilon$, chosing $\rho<\eta$, we find that, everywhere on the circle:
\begin{equation}
\frac{|f(z)-f(z_0)|}{|z-z_0|}<\frac{\epsilon}{\rho}
\end{equation}
the inequality being enforced by the numerator. Now
\begin{equation}
\oint_C\left|\frac{f(z)-f(z_0)}{z-z_0}\right|\,dz<\mathrm{Max}\left(\left|\frac{f(z)-f(z_0)}{z-z_0}\right|\right)\mathrm{Length}(C)
\end{equation}
which is $(\epsilon/\rho)\times2\pi\rho=2\pi\epsilon$, that can be made arbitrarily small, therefore the integral is zero.
The general identity that follows is known as Cauchy's integral theorem:
\begin{equation}
\label{eq:MonFeb25123517CET2013}
f(z_0)=\frac{1}{2i\pi }\oint_\mathcal{C}\frac{f(z)}{z-z_0}\,dz\,.
\end{equation}
It allows to compute straightforwardly contour integrals. For instance:
\begin{equation}
\oint\frac{ie^z}{z-1}\,dz=-2\pi\exp(1)\approx-17\,,
\end{equation}
on any path surrounding (in the trigonometric sense) the pole $z=1$ (and zero otherwise).
We have discussed already that holomorphic functions are differentiable to all orders. This can be proven with the Cauchy's integral formula that, in the same conditions as before, yield:
\begin{align}
f'(z_0)&=\frac{1}{2\pi i}\oint_\mathcal{C}\frac{f(z)}{(z-z_0)^2}\,dz\\
f(z_0)&=\frac{2!}{2\pi i}\oint_\mathcal{C}\frac{f(z)}{(z-z_0)^3}\,dz\\
&\dots\\
f^{(n)}(z_0)&=\frac{n!}{2\pi i}\oint_\mathcal{C}\frac{f(z)}{(z-z_0)^{n+1}}\,dz\\
\end{align}
We will prove the first one (others follow in a similar way by iteration of this procedure). Reminding that $f'(z)=\lim_{\Delta z\rightarrow0}(f(z+\Delta z)-f(z))/\Delta z$, we link the derivative to the integral representation by direct application of Cauchy's integral formula:
\begin{align}
\frac{f(z_0+\Delta z)-f(z_0)}{\Delta z}&=
\frac{1}{2i\pi\Delta z}\left[
\oint_\mathcal{C}\frac{f(z)}{z-(z_0+\Delta z)}\,dz
-
\oint_\mathcal{C}\frac{f(z)}{z-z_0}\,dz
\right]\\
&=
\frac{1}{2i\pi}\left[
\oint_\mathcal{C}\frac{f(z)}{(z-z_0-\Delta z)(z-z_0)}\,dz
\right]
\end{align}
and the proof concludes with taking the limit $\Delta z\rightarrow0$, showing that the right hand size converges to $\frac{1}{2i\pi}\oint_\mathcal{C}\frac{f(z)}{(z-z_0)^2}\,dz$. It would be tempting to pass to the limit at this point, what can be done for uniformly converging functions. Rather than prove the latter property, we show that
\begin{equation}
I(\Delta z)=\oint_\mathcal{C}\left[\frac{f(z)}{(z-z_0-\Delta z)(z-z_0)}-
\frac{f(z)}{(z-z_0)^2}\right]\,dz
\end{equation}
tends to zero as $\Delta z\rightarrow0$. This is done by reducing the integrand to common denominator
\begin{equation}
I(\Delta z)=\oint_{|z-z_0|=\rho}\frac{f(z)\Delta z}{(z-z_0-\Delta z)(z-z_0)^2}\,dz
\end{equation}
where we have also deformed the path of integration to a circle of radius~$\rho$ such that $|z-z_0-\Delta z|<\rho/2$. The latter condition allows us to bound $\rho=|z-z_0|=|z-z_0-\Delta z+\Delta z|$ by $|z-z_0-\Delta z|+|\Delta_z|$, and since $|\Delta_z|<|z-z_0-\Delta z|<\rho/2$, that is, $-|\Delta z|>-\rho/2$, therefore $|z-z_0-\Delta z|>\rho/2$. The function $f$ being continuous (since it is holomorphic), it has a maximum~$M$ on $C$, and the integrand of $I(\Delta z)$ satisfies:
\begin{equation}
\left|\frac{f(z)\Delta z}{(z-z_0-\Delta z)(z-z_0)^2}\right|<\frac{M|\Delta z|}{\frac{\rho}2\rho^2}
\end{equation}
from which:
\begin{equation}
I(\Delta z)<\frac{4\pi M}{\rho^2}|\Delta z|
\end{equation}
that goes to zero as $\Delta z\rightarrow 0$.
Note that we recover straightforwardly the result $\oint_\mathcal{C}\frac{dz}{(z-a)^n}=2i\pi\delta_{n,1}$ that we obtained last time from explicit calculation. This is also useful to compute contour integrals. For instance,
\begin{equation}
\oint_\mathcal{C}\frac{\cos z}{(z-i\pi)^2}\,dz=-2i\pi\sin(i\pi)=2\pi\sinh(\pi)\approx72.6\,,
\end{equation}
for $\mathcal{C}$ encircling $i\pi$, zero otherwise.
Cauchy's formula therefore shows that, in complex analysis, differentiation is equivalent to integration.
