Conformal mapping
(Lecture 10 of Mathematical Methods II.)
A conformal mapping is a transformation that preserves the angles. In 2D, a conformal mapping is one that can be represented by an holomorphic function, except where its derivative cancels. Conformal mapping is extremely useful to solve physical problems as it can remap one mathematical problem and solution in a given (easy) geometry, into another one.
The conformal transformation leaves the geometry locally identical, thanks to the angle-property. It allows for some rotation, translation, stretching, which are not apparent when looking close enough, while an angle is a scale-free property that needs to be conserved if the transformation is not to alter important features of the problem. The magnitude of stretching is measured by the Jacobian, which is a measure of how much space is rescaled in the new geometry as compared to the initial one. We remind the formal definition:
For the function $f(z)=u(x,y)+iv(x,y)$, the Jacobian $J_f(x,y)$ reads:
\begin{equation}
\label{eq:TueFeb12123308CET2013}
J_f(x,y)=\left|
\begin{matrix}
\displaystyle\frac{\partial u}{\partial x} & \displaystyle\frac{\partial u}{\partial y} \\
\displaystyle\frac{\partial v}{\partial x} & \displaystyle\frac{\partial v}{\partial y}
\end{matrix}
\right|\,,
\end{equation}
The Jacobian is thus the matrix of transformation from a set of coordinates (those derivating) to a new one (those being derivated). Its determinant represents the ratio of volumes in the old and the new coordinates. It is also commonly written as $\frac{\partial(u,v)}{\partial(x,y)}$. If the Jacobian (determinant) is not zero, the transformation is bijective. In the case of an holomorphic function $f$, from the Cauchy--Riemann equations, we get straightforwardly:
\begin{equation}
\label{eq:TueFeb12124053CET2013}
\frac{\partial(u,v)}{\partial(x,y)}=|f'(z)|^2\,,
\end{equation}
Points where $(\partial_xu)^2+(\partial_xv)^2=0$ are called critical points.
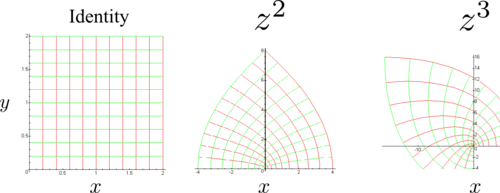
The stretching in area of the square is roughly $|f'|^2$.
Each holomorphic function, and all their possible combinations, give rise to conformal mapping. One can go through a safari of the various stretching of the complex plane. Such as:
- Exponential. The function $\exp(z)$ is a one-to-one mapping between the horizontal strip $-\pi<y\le\pi$ onto the complex plane $\mathbf{C}-\{0\}$. The patch of the grid $\{z=x+iy:a<x<b\mathrm{\ and\ }c<y<d\}$ transforms into:
$$\{\rho e^{i\theta}:e^a<\rho<e^b\mathrm{\ and\ }c<\theta<d\}\,.$$
- $(e^z-i)/(e^z+i)$. This transforms the horizontal strip $0<y<\pi$ onto the disk $|z|<1$. The $x$-axis is mapped onto the lower semicircle bounding the disk and the $y=\pi$ axis is mapped onto the upper semicircle. This follows from the decomposition $z\rightarrow\exp(z)\rightarrow(z-i)/(z+i)$ with the latter M\"obius transform mapping the upper half-plane $\Im(z)\ge0$ onto the disk $|z <1$.
- $z^n$. This maps the infinite sector of angle $\pi/m$ to the complex plane.
- $\sin(z)$. This maps the vertical strip $-\pi/2<x\le\pi/2$ into the complex plane. Since $\sin(z)=\sin x\cosh y+i\cos x\sinh y$, we find:
$$\frac{u^2}{\sin^2x}-\frac{v^2}{\cos^2x}=1\,,\qquad\frac{u^2}{\cosh^2y}+\frac{v^2}{\sinh^2y}=1\,,$$ showing that the Cartesian grid transforms into a net of hyperbolas and ellipses.
- $z+1/z$. From the polar coordinates: $w=z+1/z=(r+1/r)\cos\theta+(r-1/r)\sin\theta)$, this maps centered circles $r=\mathrm{cst}$ into ellipses.
An homotopic transformation is a continuous deformation from one transformation to another. For instance, the following shows the homotopic deformation from the inverse to the exponential, parametrized by $t$:
$$z\rightarrow\frac{1-t}{z}+t\exp(z)\,.$$
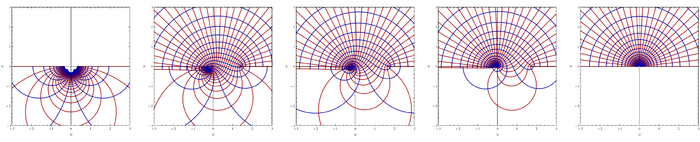
It shows how the patch $-3\le x\le 3$ and $0\le y\le\pi$ of the complex plane gets remapped from circles in the lower planes to circles and rays of an altogether different character in the upper plane.
The Schwarz-Christoffel mapping is a more general transform, that defines a conformal mapping of the upper half-plane onto the interior of a simple polygon.
The function $$f(z) = c\int\frac{dz}{(z-a_1)^{k_1}(z-a_2)^{k_2}\ldots(z-a_n)^{k_n}}+C,$$ with $a_1<a_2<\dots<a_n$ and $k_j$ real numbers such that $|k_j|\le1$, maps the real axis and the upper half-plane conformally onto the closed area bounded by a broken line. When~$z$ moves on the real axis, $f(z)$ moves along the broken line so that the direction turns the amount $k_j\pi$ anticlockwise each time time $z$ passes a point~$a_j$.
The Riemann mapping theorem states that if $U$ is a non-empty simply connected open subset of $\mathbf{C}$ (not $\mathbf{C}$ itself), then there exists a bijective and holomorphic mapping $f$ from $U$ onto the open unit disk $\{z\in\mathbf{C}\,,|z|<1\}$.
The interest of such transforms is that they transport the harmonic properties. Illustratively, if $f$ is a bijective conformal transform between two complex domains, and $\phi$ an analytic function of the variables $x$, $y$, we have $\nabla_{x,y}^2\phi=|f'(z)|^2\nabla_{u,v}^2[\phi(f^{-1}(u,v))]$, where the rhs involves the image space, in the new coordinate $u$, $v$. If we can solve a problem in one geometry, we have solved it in all geometries to which we can map conformally.
