Introducing complex numbers
(Lecture 1 of Mathematical Methods II.)
Cardano found out that Algebraic procedures provide answers that, although nonsensical for their purpose, are mathematically consistent. Divide a line of length 10 in two parts so that the area of the rectangle formed by them is 40:
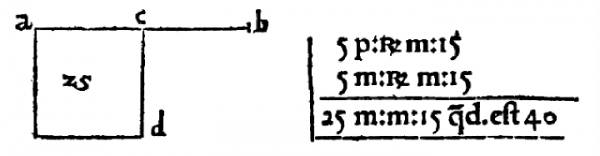
This is impossible (the area is at most 25), but a blind application of the formulas for the corresponding equation ($x(10-x)=40$) gives solutions:
$$x=5\pm\sqrt{-15}$$
that work, since $(5+\sqrt{-15})(5-\sqrt{-15})=25-(\sqrt{-15})^2=25+15=40$. Although it caused much controversies (and vexed feelings), usefulness of such a trick in an age where Mathematics was more about exploration than about contemporary rigor, eventually led to their acceptance. Euler introduced $i$ as a notation for the number who squares to $-1$ (the imaginary unit) and made the topic flourish, culminating with the so-called Euler formula to which we return in an instant. We first have to build ourselves "complex calculus" by mere "blind application" of the rules of algebra with the added rule:
$$i^2=-1\,.$$
With a complex number now defined as any number of the type
$$x+iy$$
with $x$ and $y$ two "normal" (real) numbers, we can check that everything is consistent and self-contained (we do not create new types of numbers). In particular, $z_1$ an $z_2$ being two such numbers, we have:
\begin{align}
&z_1+z_2=(x_1+x_2)+i(y_1+y_2)\,,\\ &z_1z_2=(x_1x_2-y_1y_2)+i(x_1y_2+x_2y_1)\,,\\ &z_1/z_2=z_1z_2^*/|z_2|^2\,,
\end{align}
We have used in the last line the complex conjugation, denoted with a star ($*$), that only changes the sign of $i$. By recurrences, we see that sums, products and their inverses (that can be found using, again, the same rules as real algebra) remain complex numbers, that is, of the type $x+iy$ (for instance, $i^3=-i$ and also $1/i=-i$). They form a closed set of numbers under these operations, for which we can also always find an inverse (except zero that has no inverse for the product operation). Mathematicians say that "the set $\mathbf{C}$ of Complex number is a field".
From this point onward, we will extend our knowledge and understanding of Mathematical operations with complex numbers beyond mere additions and products. For instance, when dealing with numbers, one quickly comes to the problem of computing their roots. This arose for the Greeks with the length of the diagonal of a square, another puzzling question at the time since although this number can be estimated easily (using Heron's iterative method $x_{n+1}=(x_n+s/x_n)/2$ to approach $\sqrt{s}$), the exact number cannot be written in the form $a/b$ (a fraction of two integers) which was the Greek paradigm to fill-in the gaps between the integers. We now ask, therefore, what is
- $\sqrt{i}$?
In the spirit of what we have just said, applying "blindly" the algorithm behind a mathematical definition, we could answer it pragmatically by computing:
$$1\rightarrow(1/2+i/2)\rightarrow(3/4+3i/4)\rightarrow(0.708\bar 3 + 0.708\bar3i)\rightarrow(0.7071\bar 3 + 0.7071i)$$
which has converged already (Heron's method is famous for its extremely fast convergence, doubling significant digits at each iteration). In the course of checking this result, that is, that the square of this number is $i$, we are remembered of the meaning of $\sqrt{i}$: this is the number $x+iy$ whose square is $i$. That is, set in equation:
$$(x+iy)^2=i$$
which is easily solved by usual algebra and association of real and imaginary parts together:
\begin{equation}
\begin{cases}
&x^2-y^2=0\,,\\
&2xy=1\,,
\end{cases} \end{equation}
with solutions $\pm(1+i)/\sqrt{2}$. Like for real numbers, there are two solutions. While this was a mere annoyance before, in the complex case, this will turn out to be an important feature, that we will discuss in more details in Lecture 3.
Let us look at other expressions inherited from real calculus. How to compute $\exp(z)$ with $z\in\mathbf{C}$? What is, as one would typically wonder at this point:
- $\exp(i)$?
We have to remember the definition of the exponential. From Euler again, it comes in the computation of compound interests as $\exp(x)=\lim_{n\rightarrow\infty}\left(1+\frac{x}{n}\right)^n$ and we could use this formula to compute complex exponentials. The geometric construction in the complex plane shows how a circle is constructed in this way~[1]. It is more convenient and efficient to work directly with the understanding that the exponential is a power-function, namely, that $\exp(x)=e^x$ with $e=\exp(1)$. The series expansion (starting with $d(e^x)/dx=e^x$) brings us to $e^x=\sum_{n=0}^\infty x^n/n!$ which, when applied directly to the complex numbers, yields:
$$\exp(ix)=\cos(x)+i\sin(x)\,.$$
This formula—Euler's Formula—might be the most important of complex calculus. The sine and cosine being trigonometric functions that assume particularly simple values for $x=\pi$, we arrive at the following important identities:
$$e^{i\pi}=-1,\quad e^{i\pi/2}=i,\quad\mathrm{etc.}$$
This also answers our question for what is in fact a rather unimportant number, $e^i=\cos(1)+i\sin(1)\approx 0.54+0.84i$. Note that $x$ in Euler's formula can also be complex. Like this you will find that $\cos(i)=(e^{-1}+e^{1})/2\approx 1.54$ is a real number but that, unlike a real cosine, is above 1 (we have used, again, the usual properties of the various actors involved, such as $\cos(-x)=\cos(x)$ and $\sin(-x)=-\sin(x)$).
The exponential is also the backbone for the geometric representation of complex number:
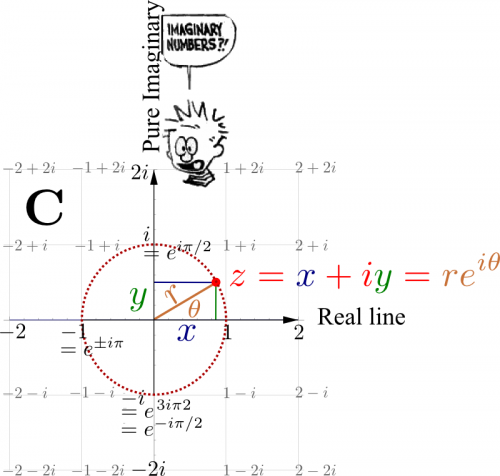
In this simple scheme, a complex $x+iy$ is plotted as a point of Cartesian coordinates $(x,y)$ in the plane. This mapping to geometry is not due to Descartes who mused a lot with complex numbers, but to Gauss and is known as the Argand space after a later advocate of this representation. By scaling (with $1/r$ where $r=zz^*=x^2+y^2$), complex numbers can be projected onto the unit circle where they become an exponential $e^{i\theta}$. This polar representation is extremely useful and powerful and should be equally familiar than the Cartesian one.
We can revisit all that we have learned about complex numbers by vizualizing them in the complex plane. For instance, under additions, complex numbers behave like vectors. This is better seen in the Cartesian picture. Under multiplications, they rotate and stretch around the plane, namely, their angles add up while their distances multiply. This is better seen in the polar picture. Multiplying by a complex exponential rotates a complex number.
A hint of the power and richness of the complex numbers can be appreciated by considering an operation as simple $z_{n+1}\rightarrow z_{n}^2+c$ (simply iterating the squaring and displacing by a complex number $c$ of $z_0=0$). If we consider the set $\mathcal{M}$ of points $c$ in the complex plane such that the iteration does not diverge (that is, such that $(((c^2+c)^2+c)^2+c)^2+\cdots$'s modulus is bounded), we arrive at the following structure (in black; white are points that escape to infinity):
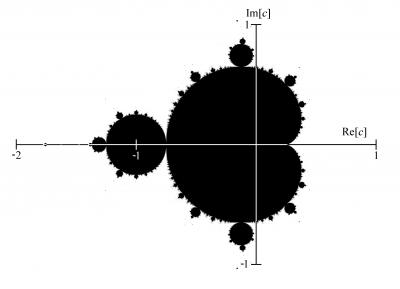
It is known as the Mandelbrot set and has been a pillar for the fractal geometry, which, interestingly, flourishes with the most elementary operations in the complex plane. With a computer in your hand, it is nowadays easy to explore this object (by mere multiplication and additions) that pioneers plotted in ASCII with * characters. If one zooms in the areas at the boundaries of the set, one literally discovers regions of unsuspected and mind boggling complexity.
We will have various occasions to ponder on the complex plane again in the course of these lectures, when it becomes the support not only of polynomials but of more complicated functions (roots and exponentials).
For today we will illustrate how it can help us in handling complex expressions. Let us see as a final example how to compute the $\log(i)$. Here again, we can use an algorithmic procedure or remember the Mathematical meaning of the logarithm. Using the latter, the log of a number $z$ is the power $x$ that raises the base $b$ of the logarithm to $z$ (technically we should write $\log_b$ and when this is not the case we understand $b=10$ or $b=e$ although in the latter case it is recommendable to write $\ln$). So $\log(i)$ is this number~$x$ such that, say, $e^x=i$, which we can solve easily by picturing the problem in the complex plane, the number $i$ is the noon of the unit circle and therefore $\log_e(i)=i\pi/2$.
In the following of this course, we will revisit in the light of complex numbers, notions of real calculus such as derivability and integrability, and find the topic to be vastly more powerful, aesthetic and elegant than its real counterpart. We will conclude this introductory lecture with general comments, particularly on the spirit proper to physicists when handling mathematical concepts (which shall be our approach, this being a course of mathematical methods for physicists).
The first point is that Complex Numbers fill in a big gap in calculus; there is something known as "the fundamental theorem of Algebra" which states that a polynomial equation of order $n$ has exactly $n$ complex roots (counting multiplicity). This means that we do not need further generalization such as introducing $i$ to solve $x^2=-1$ to solve other equations, like $x^{4}=-1$. All solution to polynomial equations are in the form $x+iy$ (and we know how many there are). It is therefore an extremely important topic that requires and deserves your full attention. It is also of extremely importance in physics, not only for technical reason, but also because, to the best of our knowledge, the universe is described at a fundamental level by complex numbers (by quantum field theory, our best theory of all). The Schrödinger equation, as the simplest case, is a complex equation: $i\partial_t\psi=H\psi$ with $\psi$ a complex function ($H$ the Hamiltonian). It does not mean that there are no generalization of them. Quite on the contrary, Hamilton (the same as the one of Hamiltonian mechanics that we met a couple of sentences ago) extended complex numbers into so-called quaternions, in much the same way complex numbers extend real numbers. Quaternions are numbers where three elements $i$, $j$ and $k$ (rather than one, $i$, in complex calculus) are introduced, with the fundamental law $i^2 = j^2 = k^2 = ijk = −1$. In quite the same way as we have done above, one can work out from there the properties of quaternions. This, however, already brings us at the research level. Quaternions are controversial and complex numbers are powerful enough to detain us in their in-depth study.
When solving a problem in physics, it is "fine" to try, to explore, to attempt a wild guess or generalization and follow the consequences. This is unlike in Mathematics where exact and accurate statements are carefully proven. We shall have on a few occasions to adopt a bit of mathematical rigor and demonstrate a result. More importantly, however, we will strive to pursue as wide and extensive an understanding as possible. This is a modern approach in theoretical physics. Just like Cardano who in 1545 allowed himself to factor out real numbers into some with negative roots, Dirac factored out the Schrödinger equation, not into complex numbers but into matrices of them, with little more than hope in the consistency of an intuitive guess. Doing so, he discovered the equation that now bears his name, the concept of antiparticles that is a relativistic consequence of quantum mechanics and put down the foundation for quantum electrodynamics, that itself blossomed into what we've just described as our best theories of all.
