Limits and continuity (for the Mathematician)
(Lecture 5 of Mathematical Methods II.)
We will take the advantage of the question of continuity of complex functions to approach the subject from a more Mathematical viewpoint than is usual for a physicist, with an inclination to rigorous proofs such as those that a Mathematician would desire.
This requires the formal introduction of abstract concepts. Because the complex plane is an already extremely particular case, we will be able to have a taste of how Mathematics deals with its subjects without entering into too many details, although we shall give one general definition to illustrate the gap between Mathematics and Physics (the understanding of continuity more from the point of view of a Physicist was the topic of the previous lecture).
A so-called topology is the first aspect to introduce to approach the problem of continuity. Essentially, topological spaces have the minimum necessary structure to allow a Mathematical definition of it.
We will survey a bit of so-called "point-set topology" (or general topology), which describes properties related to convergence, connectedness and continuity for sets of points (our set is the set of complex numbers $\mathbf{C}$). This is how a mathematician introduces it:
- Definition: A topology on a set $X$ is a pair $(X,\mathcal{J})$ with $\mathcal{J}$ a subset of $\mathcal{P}(X)$ containing at least $\emptyset$ and $X$ and which is closed under the formation of arbitrary unions and finite intersections.
Here $\mathcal{P}(X)$ is the power set (
conjunto potencia), that is, the set of all subsets of $X$.
- Definition: The members of $\mathcal{J}$ are called open sets.
This was our formal definition of general validity. It seems to say very little. This is however what powers the most general and encompassing definition of continuity from a purely Mathematical point of view:
- Definition: A function $f$ is continuous if the inverse image of every open set is open.
Let us remind that in set theory, for a function $f:X\rightarrow Y$, the inverse image $f^{-1}(B)$ of a subset $B\subset Y$ is the set $A=\{x\in X, f(x)\in B\}$.
We will now step down to an approach more suitable to physicists and later comment on the connection between this and a more "familiar" definition of continuity.
The complex plane $\mathbf{C}$ is also a metric space, that is, a set where a distance can be defined.
- Definition: A distance on a space $X$ is a function $d(x,y)$ such that:
- $d(x,y)=d(y,x)$,
- $d(x,y)=0\Leftrightarrow x=y$,
- $d(x,z)\leqslant d(x,y)+d(y,z)$.
In the case of the complex plane, the canonical distance is the modulus $d(x,y)=|x-y|$.
- Definition: An open ball $B(a,r)$ of radius $r$ centered on $a$ is the set of points $B(a,r)=\{z\in\mathbf{C} \mid |z,a|<r \}$.
A closed ball is one that replaces $<$ with $\leq$; that is, it includes its boundary.
In such a topology induced by the distance (this is the official terminology and the standard way to define a topology on a normed vector space), an open set is any set which is an union of open balls. The union is arbitrary, it can be infinite. According to the axioms of the topology, intersections of them must, however, remain finite to still be open.
A closed set is a set whose complement is open. A set which is both closed and open is called a clopen set.
Open sets are important for problems of convergence.
- Definition: A point $\zeta$ is an accumulation point of a subset $A$ of $\mathbf{C}$, if any open ball $B(\zeta,r)$ contains at least one point of $A$ distinct from $\zeta$.
We are almost there:
- Definition: A neighbourhood $\mathcal{V}$ of a point $z$ is a set such that there exists an open set $O$ that contains $z$ and is included in $\mathcal{V}$.
The connection with the formal definition becomes clearer with this proposition:
- Proposition: A function $f$ is continuous at the point $z$ iff for any neighborhood $\mathcal{V}$ of $f(x)$, there is a neighborhood $\mathcal{U}$ of $x$ such that $f(\mathcal{U})\subset\mathcal{V}$.
The vivid picture is that continuity means that no matter how closely we tie around $f(z)$ by reducing the neighborhood around, there is always a whole neighborhood $\mathcal{U}$ containing $z$, but also all the points in the neighborhood, that maps inside $\mathcal{V}$.
For a metric space it's enough to consider open balls. In this particular case, the continuity of $f$ at a given point $z_0$ becomes, in logical symbols:
$$(\forall\epsilon>0)(\exists\delta>0)(|z-z_0|<\delta\Rightarrow|f(z)-f(z_0)|<\epsilon)\,.$$
A funtion $f$ is continuous if it is continuous everywhere. In logical symbols:
$$(\forall z \in\mathbf{C})(\forall \varepsilon > 0)(\exists \eta > 0)(\forall w \in \mathbf{C})(|z-w| < \eta \ \Rightarrow \ |f(z)-f(w)| <\varepsilon)\,.$$
This is known as the Weierstrass definition of continuity, and is the one typically familiar to the Physicist. Note that, as typical of a Mathematical statement, the exact positioning of the closes (parentheses) and their individual statements are of paramount importance. In fact, the slightly modified:
$$(\forall \varepsilon > 0)(\exists \eta > 0)(\forall z \in\mathbf{C})(\forall w \in \mathbf{C})(|z-w| < \eta \ \Rightarrow \ |f(z)-f(w)| <\varepsilon)$$
describes a stronger version of continuity, known as "uniform continuity".
Continuity, as brought down from its Mathematical meaning to the version suitable for us Physicists, is thus, in fact, expressed through the notion of limit. Remembering that:
- Definition: The sequence of points $z_n$ converge to $z_0$, and we write $\lim_{n\rightarrow\infty}z_n=z_0$ if:
$$(\forall\epsilon>0)(\exists N\in\mathbf{N})(\forall n\in\mathbf{N})(n>N\Rightarrow|z_n-z_0|<\epsilon)$$
Remembering that a function $f$ converges to $l$ at $z_0$ iff $(\forall\epsilon>0)(\exists\eta>0)(\forall z\in\mathbf{C})(|z-a|<\eta\Rightarrow|f(z)-l|<\epsilon)$, we see that continuity corresponds to $\lim_{z\rightarrow z_0}f(z)=f(z_0)$. Effectively, a function $f$ is continuous if and only if it preserves the limits of sequences.
Another important
- Definition: A Cauchy sequence $(z_n)$ is one such that:
$$(\forall\epsilon>0)(\exists N\in\mathbf{N})(\forall p,q\in\mathbf{N})(q,p\ge N\Rightarrow|z_p-z_q|\le\epsilon)\,.$$
A converging sequence is of Cauchy. The important point is the reciprocal. When this is the case for every Cauchy sequence, the space is said to be "complete". The complex plane is complete (because $\mathbf{R}$, out of which it is constructed, is; $\mathbf{Q}$ is not).
At this point a Mathematician would proceed with proving theorem from the above definitions and the rules of logic, such as, if $f$ and $g$ are two continuous functions, $f+g$, $fg$ and $f\circ g$ are also continuous. $f/g$ is continuous except on points where $g=0$. If $f$ is continuous, so are its real and imaginary parts. Etc. They would do it at the formal and abstract level of most general validity. We would find the particular case that is both the most simple and the most powerful for our purposes, such as the Weierstrass (also called, $\delta$-$\epsilon$) formulation, and parallel their results with the lesser tools. The deeper and more fundamental becomes a subject, the closer become the two approaches. When it comes to integration, for instance, the Mathematical theory starts in measure theory with the concept of a $\sigma$-algebra (the counterpart of a topology for notions of convergence and continuity). A $\sigma$-algebra (
une tribu, a tribe) on $C$ is a collection $\Sigma$ of subsets of $X$ that contains $X$ and that is closed under the complement and countable unions of its members. The general definition looks equally abstract and remote from what defines the problems of integration. This is however what allows to build Lebesgue integrals, that are a generalization of the familiar (Riemann) integrals, sometimes needed also in physics. We will not delve again into the Mathematical point of view of such problems, and when the need arise, we will introduce "hand-waving tricks", such as the Dirac $\delta$ function instead of a Schwartz distribution (that allows through Lebesgue theory to derivate discontinuous functions). But it is important to know that such a Mathematical approach exists and how it looks like.
We will also need, later, more notions proper to the topology of the space, regardless of any function. We introduce the most important and representative here:
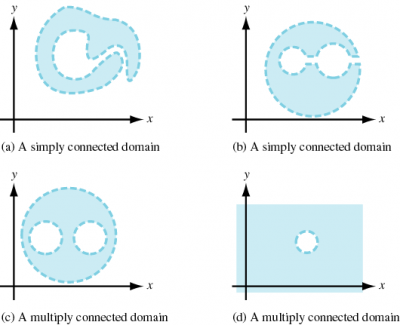
- Definition: A domain $D$ is an open set such that any two points can be connected by a broken line segment in $D$. A domain $C$ is convex if any two points can be joined by a straight line in $C$. A domain is path-connected if a path can be drawn between any two points in the space. It is furthermore simply connected if every path between two points can be continuously transformed, staying within the space, into any other path while preserving the two endpoints in question.
