Mathematical Methods II
Computed in class (edition 2013) during the "computer session" to answer Problem II of handout 7: the area of the Mandelbrot set in the region $\mathrm{Re}(z)\ge 0\approx2\times 0.2$ (the later figure is computed by pixel counting on the figure here displayed).
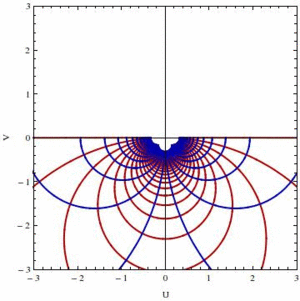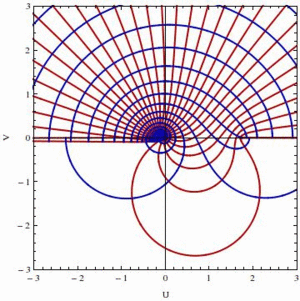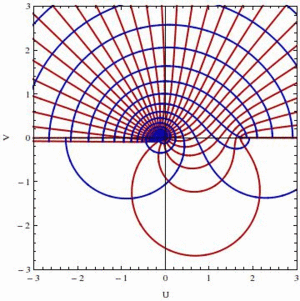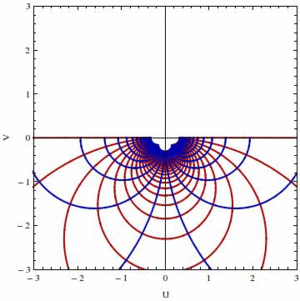
Homotopic transformation $(1-t)/z+t\exp(z)$ of the rectangular patch of $\mathbf{C}$ defined by $-3\le x\le 3$ and $0\le y\le\pi$ as function of $t$, showing how straight lines are remapped into circles of different natures in both half-planes of $\mathbf{C}$. Part of an home exam (edition 2014).
This page gathers informations and material related to my course MÉTODOS MATEMÁTICOS II at the Universidad Autónoma de Madrid.
Lectures
The content leaves room for 3 to 5 sessions devoted to buffering the material (longer lectures), accommodating "All Questions Answered" sessions and revisiting material in need of attention before the exams.
Each lecture is accompanied by a two-hour exercises sessions. Lecture 19 is delivered as a Seminar, i.e., at a higher pace, jumping over intermediate results, no taking feedback from the audience and presenting more advanced material.
- Introducing Complex Numbers · handout 1.
- Complex functions of complex numbers · handout 2.
- Exponentials, trigonometric functions, hyperbolics and their inverses · handout 3.
- Limits and continuity (for the Physicist) · handout 5.
- Limits and continuity (for the Mathematician) · handout 6.
- Derivatives and analyticity · handout 7.
- Differentiability and Cauchy-Riemann · handout 8.
- Harmonic functions and Laplace's equation · handout 9.
- Complex Potentials · handout 10.
- Conformal mapping · handout 11.
- The Möbius Transformation · handout 12.
- Integrals in the complex plane · handout 13.
- Line and contour integrals · handout 14.
- The Cauchy-Goursat theorem and its integral forms · handout 15.
- Consequences of the Cauchy theorem · handout 16.
- Series of Complex Numbers · handout 17.
- Power Series · handout 18.
- Uniform convergence · handout 19.
- "Seminar": Analytic functions and continuation · (no handout).
- Taylor Series · handout 20.
- Laurent Series · handout 21.
- Singularities · handout 22.
- Residues · handout 23.
- Applications of Residue Theory · handout 24.
- Fourier Series · handout 25.
- Summation of Series · handout 26.
- The Riemann and the Bloch Spheres · handout 27.