m (Created page with "= Two particles in 1D = {{stub}} <center><wz tip="The joint probability distribution for the position two non-interacting 1D particles in the square well: one in the ground s...") |
m (→Two particles in 1D) |
||
| Line 1: | Line 1: | ||
= Two particles in 1D = | = Two particles in 1D = | ||
| − | |||
| − | <center><wz tip="The joint probability distribution for the position two non-interacting 1D particles in the square well: one in the ground state, the other excited, as a function of their statistics.">[[File:Screenshot_20210323_204045.png| | + | We carry on our program of considering several quantum objects at once. We have studied a lot the single particle, for instance in various potential wells (square well, delta well, etc.) This was mainly in 1D, in which case the wavefunction was $\psi(x,t)$ with the modulus square giving the density of probability to find the particle at position $x$ at time $t$. We also considered a particle in 2D or 3D. For the 2D case, for instance, we upgraded the wavefunction to $\psi(x,y,t)$ with the modulus square giving the density of probability to find the particle at position $(x,y)$ at time $t$. We now return to the 1D case (for simplicity), but with two particles. Maybe surprisingly, this will turn out to be very connected to the 2D case of a single particle: |
| + | |||
| + | <center>two 1D particle ~ one 2D particle!</center> | ||
| + | |||
| + | We can still apply the same trick of separation of variables for the space and time coordinates, so we will get rid of time in the following. Solving for the eigenstates will yield the most general solution by linear superpositions. | ||
| + | |||
| + | Therefore, we now consider the eigenstates of two 1D particles. Instead of $(x,y)$, we will write $(x_1,x_2)$ to highlight that the variables correspond to the $x$-positions (on the same axis) of two particles. In this case, their joint wavefunction reads: | ||
| + | |||
| + | $\psi(x_1,x_2)$ | ||
| + | |||
| + | and their respective operators act on the corresponding slices of the Hilbert tensor product, e.g., the kinetic energy is $-\hbar^2\partial_{x_1}/(2m_1)$ for particle 1 (assuming it has a mass $m_1$) and $-\hbar^2\partial_{x_2}/(2m_2)$ for particle 2 (with mass $m_2$). The same holds for the position operators, which are $x_1$ and $x_2$, respectively. | ||
| + | |||
| + | The potential can also have some effect on one particle only (if they aren say, of different type, e.g., one is charged and feels an electrostatic potential while the other is not and does not feel it). In this case, such a potential applies only to the corresponding slice of the tensor product, and carries along the identity for the other part that concerns the other particle. If both particles feel the same potential, then it is symmetric. As a result, assuming such a case and also that both particles have the same mass, $m_1=m_2$, then we find, interestingly, that the two 1D particle Schrödinger equation | ||
| + | |||
| + | $$-i\hbar\partial_t\psi(x_1,x_2,t)=\left[-{\hbar^2\over2m}(\partial_{x_1}+\partial_{x_2})+V\right]\psi(x_1,x_2,t)$$ | ||
| + | |||
| + | is exactly the same, as far as the mathematical structure is concerned, than for one 2D particle, since indeed $\partial_{x_1}+\partial_{x_2}=\nabla^2$ (we would write $x$ and $y$ rather than $x_1$ and $x_2$ for a 2D particle, but this is just an irrelevant notation: the equation is the same). | ||
| + | |||
| + | This is welcome since we have already solved many one 2D-particle problems... so it seems that much of the work has been done already. And this is indeed the case, but there is one axiom or postulate more that we need to take into consideration. The function does not factorize in general, i.e., $\psi(x_1,x_2)$ is different from $\psi_1(x_1)\psi_2(x_2)$ and the former is what describes the two particles together, as per the tensor products rules). When it is the case that $\psi(x_1,x_2)\neq \psi_1(x_1)\psi_1(x_2)$, then the particles have correlations or are correlated. This can be induced by interactions, typically. But there is a more fundamental source of "correlations" in quantum mechanics. | ||
| + | |||
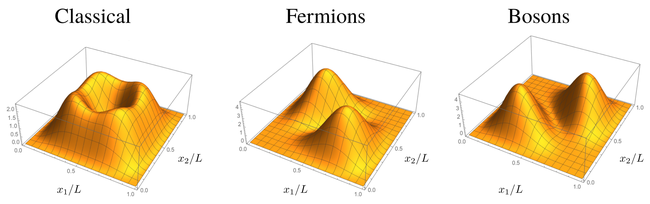
| + | <center><wz tip="The joint probability distribution for the position two non-interacting 1D particles in the square well: one in the ground state, the other excited, as a function of their statistics.">[[File:Screenshot_20210323_204045.png|650px]]</wz></center> | ||
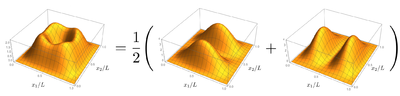
<center><wz tip="How the classical distribution is obtained from classical indeterminacy.">[[File:Screenshot_20210323_204210.png|400px]]</wz></center> | <center><wz tip="How the classical distribution is obtained from classical indeterminacy.">[[File:Screenshot_20210323_204210.png|400px]]</wz></center> | ||
{{WLP11}} | {{WLP11}} | ||
Revision as of 15:02, 21 March 2023
Two particles in 1D
We carry on our program of considering several quantum objects at once. We have studied a lot the single particle, for instance in various potential wells (square well, delta well, etc.) This was mainly in 1D, in which case the wavefunction was $\psi(x,t)$ with the modulus square giving the density of probability to find the particle at position $x$ at time $t$. We also considered a particle in 2D or 3D. For the 2D case, for instance, we upgraded the wavefunction to $\psi(x,y,t)$ with the modulus square giving the density of probability to find the particle at position $(x,y)$ at time $t$. We now return to the 1D case (for simplicity), but with two particles. Maybe surprisingly, this will turn out to be very connected to the 2D case of a single particle:
We can still apply the same trick of separation of variables for the space and time coordinates, so we will get rid of time in the following. Solving for the eigenstates will yield the most general solution by linear superpositions.
Therefore, we now consider the eigenstates of two 1D particles. Instead of $(x,y)$, we will write $(x_1,x_2)$ to highlight that the variables correspond to the $x$-positions (on the same axis) of two particles. In this case, their joint wavefunction reads:
$\psi(x_1,x_2)$
and their respective operators act on the corresponding slices of the Hilbert tensor product, e.g., the kinetic energy is $-\hbar^2\partial_{x_1}/(2m_1)$ for particle 1 (assuming it has a mass $m_1$) and $-\hbar^2\partial_{x_2}/(2m_2)$ for particle 2 (with mass $m_2$). The same holds for the position operators, which are $x_1$ and $x_2$, respectively.
The potential can also have some effect on one particle only (if they aren say, of different type, e.g., one is charged and feels an electrostatic potential while the other is not and does not feel it). In this case, such a potential applies only to the corresponding slice of the tensor product, and carries along the identity for the other part that concerns the other particle. If both particles feel the same potential, then it is symmetric. As a result, assuming such a case and also that both particles have the same mass, $m_1=m_2$, then we find, interestingly, that the two 1D particle Schrödinger equation
$$-i\hbar\partial_t\psi(x_1,x_2,t)=\left[-{\hbar^2\over2m}(\partial_{x_1}+\partial_{x_2})+V\right]\psi(x_1,x_2,t)$$
is exactly the same, as far as the mathematical structure is concerned, than for one 2D particle, since indeed $\partial_{x_1}+\partial_{x_2}=\nabla^2$ (we would write $x$ and $y$ rather than $x_1$ and $x_2$ for a 2D particle, but this is just an irrelevant notation: the equation is the same).
This is welcome since we have already solved many one 2D-particle problems... so it seems that much of the work has been done already. And this is indeed the case, but there is one axiom or postulate more that we need to take into consideration. The function does not factorize in general, i.e., $\psi(x_1,x_2)$ is different from $\psi_1(x_1)\psi_2(x_2)$ and the former is what describes the two particles together, as per the tensor products rules). When it is the case that $\psi(x_1,x_2)\neq \psi_1(x_1)\psi_1(x_2)$, then the particles have correlations or are correlated. This can be induced by interactions, typically. But there is a more fundamental source of "correlations" in quantum mechanics.