Addition of spin
(Part of the Wolverhampton Lectures of Physics's Quantum Physics Course)
We now start the program for the next several lectures of combining quantum objects (combining particles, combining oscillators, etc.) Today we start with combining spins. We remind you that the general state of spin is $|sm\rangle$ with $s$ the total spin (fixed, or constant, for a given particle, variable, as a degree of freedom for rotation in space) and $m$ is the $z$-projection of the spin, and that we have:
\begin{align}
S^2|sm\rangle&=\hbar^2 s(s+1)|sm\rangle\\ S_z|sm\rangle&=\hbar m|sm\rangle
\end{align}
Let us start with the simplest case, the two-level system, or spin 1/2.
We also remind you that $\vec S=S_x\hat i+S_y\hat j+S_z\hat k$ where the $S_k$ for $k=x,y,z$ are proportional to the Pauli matrices:
$$S_x={\hbar\over2}\begin{pmatrix}0&1\\1&0\end{pmatrix}\,,\quad S_y={\hbar\over2}\begin{pmatrix}0&-i\\i&0\end{pmatrix}\,,\quad S_z={\hbar\over2}\begin{pmatrix}1&0\\0&-1\end{pmatrix}\,.$$
So let us say that we have two 1/2-spins, in the respective (general) states $|\chi_1\rangle$ and $|\chi_2\rangle$. Since this is spin-1/2, that's for an intrinsic object and is thus of constant magnitude. This could be, for instance, the spin of two electrons, or the spin of one electron and the spin of a proton (which is also a fermion with spin 1/2), for instance in an hydrogen atom. That's it, to fix ideas, let us say we study the spin of an hydrogen atom!
The canonical basis (in the $z$-axis) for each spin is:
$$\mathcal{C}=\{ |\uparrow\rangle\,,\quad |\downarrow\rangle\}\,.$$
which means that, in general, the first spin, say of the proton, has the state
$$|\chi_1\rangle=\alpha_1|\uparrow\rangle+\beta_1|\downarrow\rangle$$
with $|\alpha_1|^2+|\beta_1|^2=1$, and that the second spin, of the electron, similarly has:
$$|\chi_2\rangle=\alpha_2|\uparrow\rangle+\beta_2|\downarrow\rangle$$
with $|\alpha_2|^2+|\beta_2|^2=1$. We used the same notation $|\uparrow\rangle$, $|\downarrow\rangle$ for the spins of the two "objects". Does it mean it is really the same? Actually not: it means the structure is the same, but really we should be writing something like:
$$\begin{align} |\chi_1\rangle^{(1)}&=\alpha_1|\uparrow\rangle^{(1)}+\beta_1|\downarrow\rangle^{(1)}\,,\\ |\chi_2\rangle^{(2)}&=\alpha_2|\uparrow\rangle^{(2)}+\beta_2|\downarrow\rangle^{(2)}\,. \end{align}$$
Notice how the "which-object" index also applies to the left-hand side, because this information cannot be on $\chi$ alone since the second spin could be in the state of the first one and vice-versa (for instance in the process of swapping their quantum state, which is actually a standard thing to do with qubits). But there is, usually, no need to, because when we bring the two spins together, the order in which we write them will tell us which object we refer to, namely, we will write the total spin as:
$$|\chi_1\rangle|\chi_2\rangle$$
and to simplify even further, we wll even put everybody in the same ket:
$$|\chi_1\chi_2\rangle\,.$$
All these are shortcuts or notations for the real mathematical structure which we are dealing with, which is a so-called tensor product $|\chi_1\rangle\otimes|\chi_2\rangle$ of the two Hilbert spaces of the two spins. Each belongs to a given vector space. The technical details don't need to worry us as long as the underlying idea is clear enough: these objects now come to play together. And we'll see how their algebra work. It's easy, it works the intuitive way.
So if you have
$$|\uparrow \downarrow\rangle$$
that means the proton points up, and the electron points down. On the other hand,
$$|\downarrow\uparrow\rangle$$
means the proton is down and the electron is up.
This state:
$$|\chi_2\chi_1\rangle$$
means that the proton is in the state $|\chi_2\rangle^{(1)}$ (we put back the index now as it's required to lift the ambiguity!) and the electron in the state $|\chi_1\rangle^{(2)}$. Make sure that you appreciate the full subtleties here!
Clearly the basis for the two-spin compound is:
$$\mathcal{C}_2=\{|\uparrow\uparrow\rangle\,,\quad |\uparrow\downarrow\rangle\,,\quad |\downarrow\uparrow\rangle\,,\quad |\downarrow\downarrow\rangle\}\,.=,$$
and as you can guess, the general spin-state of the hydrogen (or any two spin-1/2 objects) is:
$$|\Psi\rangle=\alpha_{\uparrow\uparrow}|\uparrow\uparrow\rangle+\alpha_{\uparrow\downarrow}|\uparrow\downarrow\rangle+\alpha_{\downarrow\uparrow}|\downarrow\uparrow\rangle+ \alpha_{\downarrow\downarrow}|\downarrow\downarrow\rangle\,,$$
with, e.g., $|\alpha_{\uparrow\downarrow}|^2$ the probability to have the proton in the up spin and the electron in the down spin.
Now the question becomes, collectively, as a spin itself, what is $|\Psi\rangle$? Is it a $|sm\rangle$ spin? If so, what is $s$ (total magnitude of the resulting spin), and what is the associated $m$ ($z$-projection)? That is to say, if we have two little spin 1/2, how do they spin together, what is the total spin they team-up with, if any?
To figure this out, we need to go from the states, to the operators. The total spin will be, on physical grounds and based on classical principles:
$$\vec S\equiv \vec S^{(1)}+\vec S^{(2)}\,.$$
The total spin adds in quantum mechanics because it is how angular momentum (and remember spin is a sort of "intrinsic angular momentum") behaves in classical mechanics: vector addition! Note that we need to label the operator (the proton spin and the electron spin, respectively), to know to which part of the ket they apply. Besides, although the sum is commutative, but the product is not, the order could matter in general. So we have, if we break the above equation into its components:
\begin{align} S_x&=S^{(1)}_x+S^{(2)}_x\,,\\ S_y&=S^{(1)}_y+S^{(2)}_y\,,\\ S_z&=S^{(1)}_z+S^{(2)}_z\,. \end{align}
The $z$-component is particularly important because it is the $m$-part of the spin. So let us compute
$$S_z|\chi_1\chi_2\rangle=(S^{(1)}_z+S^{(2)}_z)|\chi_1\chi_2\rangle$$
assuming for now that $\chi_i$ refer to basis states (if we know what a linear operator does on the basis, we know what it does for all states). Now how does this work? As we said: intuitively: the ${}^{(1)}$ operator works on its vector-space (the one we write first, so on the left), and the ${}^{(2)}$ operator works on its vector-space (the one we write second, on the right). We could, for clarity, spell out explicitely what the other operator for the other spin is doing: nothing! that's the identity. We would write:
\begin{align} S^{(1)}_z&=S^{(1)}_z\otimes\mathbb{1}\,,\\ S^{(2)}&=\mathbb{1}\otimes S^{(2)}_z\,. \end{align}
And then each spin gets its operator when distributing them onto the states: $$(S^{(1)}_z\otimes\mathbb{1})|{\chi_1\chi_2}\rangle= (S^{(1)}_z|\chi_1\rangle)\otimes(\mathbb{1}|\chi_2\rangle)$$. Everybody's a winner! We sometimes keep the tensor notation, to keep track which operator applies to which part of the Hilbert space, but if there is no confusion, it is clearly more convenient to drop it.
So, back to our total spin, we have:
$$(S^{(1)}_z+S^{(2)}_z)|\chi_1\chi_2\rangle = \color{red}{[S^{(1)}_z|\chi_1\rangle]}|\chi_2\rangle+|\chi_1\rangle\color{blue}{[S^{(2)}_z|\chi_2\rangle]}\,.$$
Now, given the commutation of constants with vectors, and factorizing the common bits (and getting rid of the colors), putting everything back together, we find:
$$(S^{(1)}_z+S^{(2)}_z)|\chi_1\chi_2\rangle = \hbar(m_1+m_2)|\chi_1\chi_2\rangle\,.$$
Just like in classical mechanics, the ^^z-component of the angular momentum adds. The algebra is working so that this property gets carried into the quantum realm. So for our two spin-1/2 systems, we then have the possibilities:
$$\begin{align}
|\uparrow\uparrow\rangle & \hbox{ has $m={1\over2}+{1\over2}=1$}\,,\\
|\uparrow\downarrow\rangle & \hbox{ has $m={1\over2}+{-1\over2}=0$}\,,\\
|\downarrow\uparrow\rangle & \hbox{ has $m={-1\over2}+{1\over2}=0$}\,,\\
|\downarrow\downarrow\rangle & \hbox{ has $m={-1\over2}+{-1\over2}=-1$}\,.
\end{align}$$
Since $m$ goes from $-1$ to $1$ by integer steps, it seems our compound spin has total spin 1. Not quite, though... Note that the progression is not $-1, 0, 1$, but $-1, 0, 0, 1$... so we've got a departure from the usual spin ladder. Why is that? Let's find out by constructing the states with the construction operators. We start at the bottom of the ladder. Clearly, it is:
$$|\downarrow\downarrow\rangle$$
Let's climb. We apply the "add-one-quantum-of-$z$-angular-momentum" operator which we can expect will simply add this quantum to one or to the other, thus as a sum. If it would be a product, we'd add two quanta, which is not what we want, and we cannot add less than a unit, this is quantum-mechanics after all, so the only reasonable option is to distribute it in this way:
$$S_+=S_+^{(1)}+S_+^{(2)}$$
where, remember, $S_+|\downarrow\rangle=\hbar|\uparrow\rangle$ and $S_+|\uparrow\rangle=0$. These, applying on single spins, are normalized, while the expression above is clearly not as we did not take into account the probability of which spin gets the full quantum, that, for symmetry, will clearly be 1/2, so we can expect a $1/\sqrt2$ to pop-up at some point, as we shall indeed confirm shortly.
Algebra works in the same, intuitive way:
\begin{align}
S_+|\downarrow\downarrow\rangle&=(S_+^{(1)}+S_+^{(2)})|\downarrow\downarrow\rangle\,,\\
&=(S_+^{(1)}|\downarrow\rangle)|\downarrow\rangle+|\downarrow\rangle S_+^{(2)}|\downarrow\rangle\,,\\
&=(\hbar|\uparrow\rangle)|\downarrow\rangle+|\downarrow\rangle(\hbar|\uparrow\rangle)\,,\\
&=\hbar(|\uparrow\downarrow\rangle+|\downarrow\uparrow\rangle)\,.
\end{align}
The next state in the ladder is a superposition of the spin states! Creation operators do not normalize the states, so let us do this now (and here comes our expected normalizing constant):
$${1\over\sqrt{2}}(|\uparrow\downarrow\rangle+|\downarrow\uparrow\rangle)\,.$$
This type of states is very important in quantum mechanics. You might say this is one of the most, if not the most, important feature of the theory. It is called an "entangled state", because it mingles together the spins of the two particles. That's how two spins can get a $z$-projection of 0 out of two 1/2 particles: one gets the spin up and the other the spin down, with equal probability, but we do not know which one! Let us carry-on the construction, and apply $S^+$ to this zero-$z$-projection state:
$$S_+{1\over\sqrt{2}}(|\uparrow\downarrow\rangle+|\downarrow\uparrow\rangle)= {1\over\sqrt{2}}(S_+^{(1)}|\uparrow\downarrow\rangle+S_+^{(1)}|\downarrow\uparrow\rangle+S_+^{(2)}|\uparrow\downarrow\rangle+S_+^{(2)}|\downarrow\uparrow\rangle) $$
and clearly, e.g., $S_+^{(1)}|\downarrow\uparrow\rangle=|\uparrow\uparrow\rangle$, while $S_+^{(2)}|\downarrow\uparrow\rangle=0$, so working out the sum above, we find:
$$S_+{1\over\sqrt{2}}(|\uparrow\downarrow\rangle+|\downarrow\uparrow\rangle)= {2\over\sqrt{2}}|\uparrow\uparrow\rangle$$
so after renormalizing (that get rids of the constant, since there's only one state, its probability becomes 100%. Note that if we had carried the normalization with the operator we would have arrived there directly), we find the spin-1 -projection of the compound is simply both spin aligned up, as could be expected. We have disentangled the state.
If we come back to our initial ladder, we got rid of the problem of having two zeros: they entangled the state! This is a recurrent theme in quantum mechanics. When something can take two values, that leads to a linear superposition, which lifts the "which-path" or "which-way" information of having to decide on one particular outcome. So our ladder is:
$$\begin{align}
1 &\quad\text{for}& |\uparrow\uparrow\rangle\\
0 &\quad\text{for}& {1\over\sqrt{2}}(|\downarrow\uparrow\rangle+|\uparrow\downarrow\rangle)\\
-1 &\quad\text{for}& |\downarrow\downarrow\rangle
\end{align}$$
meaning that our compound object has spin
$$|1m\rangle$$
with $m=-1, 0, 1$. That's a spin 1 particle!
Let us check if it's true. By spin algebra $ S^2|sm\rangle=\hbar^2 s(s+1)|sm\rangle$, we should have
$$S^2|1m\rangle=2\hbar^2 |1m\rangle$$
and since
$$S^2=\vec S\cdot\vec S=(\vec S^{(1)}+\vec S^{(2)})\cdot(\vec S^{(1)}+\vec S^{(2)})=(S^{(1)})^2+(S^{(2)})^2+2\vec S^{(1)}\cdot\vec S^{(2)}$$
we just need to meticulously compute. We know the single-spin square from the previous lectures and the top of the page, namely:
\begin{align}
(S^{(i)})^2|\uparrow\rangle&={3\over 4}\hbar^2|\uparrow\rangle\\
(S^{(i)})^2|\downarrow\rangle&={3\over 4}\hbar^2|\downarrow\rangle
\end{align}
for $i=1,2$, so we just have to compute $\vec S^{(1)}\cdot\vec S^{(2)}=S_x^{(1)}S_x^{(2)}+S_y^{(1)}S_y^{(2)}+S_z^{(1)}S_z^{(2)}$.
We know the action of an operator on any state if we know its action on the basis vectors, so we can compute it on $\mathcal{C}_2$, which means four combinations. We start with $|\uparrow\uparrow\rangle$:
$$\vec S^{(1)}\cdot\vec S^{(2)}|\uparrow\uparrow\rangle = S_x^{(1)}|\uparrow\rangle S_x^{(2)}|\uparrow\rangle+S_y^{(1)}|\uparrow\rangle S_y^{(2)}|\uparrow\rangle+S_z^{(1)}|\uparrow\rangle S_z^{(2)}|\uparrow\rangle$$
and, remembering the single-spin Pauli matrices (also at the top of the page), we find:
$$\vec S^{(1)}\cdot\vec S^{(2)}|\uparrow\uparrow\rangle = (\hbar/2)^2\left[|\downarrow\rangle|\downarrow\rangle+(-i)^2 |\downarrow\rangle |\downarrow\rangle+(-1)^2|\uparrow\rangle |\uparrow\rangle\right] =(\hbar/2)^2|\uparrow\rangle |\uparrow\rangle$$
and putting everybody together, we have therefore
$$S^2|\uparrow\uparrow\rangle={3\over 4}\hbar^2|\uparrow\uparrow\rangle+{3\over 4}\hbar^2|\uparrow\uparrow\rangle+2\times{\hbar^2\over 4}|\uparrow\rangle |\uparrow\rangle ={2\hbar^2}|\uparrow\uparrow\rangle\,.$$
That confirms already, by the way, that $S^2|11\rangle=2\hbar^2|11\rangle$. To complete the general case, we let you compute for yourself that:
$$\begin{align}
\vec S^{(1)}\cdot\vec S^{(2)}|\uparrow\downarrow\rangle&={\hbar^2\over4}(2|\downarrow\uparrow\rangle-|\uparrow\downarrow\rangle)\\
\vec S^{(1)}\cdot\vec S^{(2)}|\downarrow\uparrow\rangle&={\hbar^2\over4}(2|\uparrow\downarrow\rangle-|\downarrow\uparrow\rangle)
\end{align}$$
and since it is straightforwardly found that $S^2|\uparrow\downarrow\rangle={3\over4}\hbar^2|\uparrow\downarrow\rangle$, $S^2|\downarrow\uparrow\rangle={3\over4}\hbar^2|\downarrow\uparrow\rangle$ and $S^2|\downarrow\downarrow\rangle={3\over4}\hbar^2|\downarrow\downarrow\rangle$, this achieves to confirm that $S^2|1m\rangle=2\hbar^2 |1m\rangle$, QED.
So it seems that we have completed our program for today. The spin of our compound two spin-1/2 object is another spin-1 object. Again, not quite, though. There is a gap somewhere... which is down to linear algebra, i.e., the mathematical structure of the theory. In the separate-objects basis, we have four vectors. Remember the basis $\mathcal{C}_2=\{|\uparrow\uparrow\rangle\,,\quad |\uparrow\downarrow\rangle\,,\quad |\downarrow\uparrow\rangle\,,\quad |\downarrow\downarrow\rangle\}$. That is indeed the dimension of the tensor products of two vector spaces of dimension 2, which is written in funny-looking tensor-product notations:
$$2\otimes 2=4$$
But after all our work, we found out that we can express this spin with three states only:
$$\{|1,-1\rangle\,,\quad|1,0\rangle\,,\quad|1,1\rangle\}\,.$$
That may make sense to you as a physical thing, but it does not as a mathematical thing. We are missing one dimension, one degree of freedom, one state! It goes back to the fact that our $|1,0\rangle$ state absorbed two vectors at once; that is where we reduced two dimensions to one... So let us look for our missing state as the perpendicular one to $|1,0\rangle$. This is the state in $\mathcal{C}_2$, whose most general version is $|\Psi\rangle=\alpha_{\uparrow\uparrow}|\uparrow\uparrow\rangle+\alpha_{\uparrow\downarrow}|\uparrow\downarrow\rangle+\alpha_{\downarrow\uparrow}|\downarrow\uparrow\rangle+ \alpha_{\downarrow\downarrow}|\downarrow\downarrow\rangle\,,$ such that
$$\langle\Psi|1,0\rangle=0\,.$$
Since
$$\langle ij|kl\rangle=\langle i|k\rangle\langle j|l\rangle=\delta_{ik}\delta_{jk}$$
the perpendicular condition gives us $\alpha_{\uparrow\uparrow}=\alpha_{\downarrow\downarrow}=0$ and $\alpha_{\uparrow\downarrow}=-\alpha_{\downarrow\uparrow}=1/\sqrt{2}$ (the latter by normalization). This is our remaining, missing state:
$$|00\rangle={1\over\sqrt{2}}(|\uparrow\downarrow\rangle-|\downarrow\uparrow\rangle)\,.$$
We called it such because you can easily check that $S^2|00\rangle=0$ (making $s=0$ and consequently $m=0$). This is the no-spin binding of the two spin 1/2: when they $\pi$-lock their phase. With no dephasing, they realize instead the $z=0$ projection of a $s=1$ effective spin.
The $|1m\rangle$ states are called "triplet states" and the state $|00\rangle$ is called the "singlet state". And that completes our picture. At least for the case of two spins of magnitude 1/2. They can combine either as a spin 1 (with three possible projections of spin) or a spin 0 particle!
The general problem is to combine several spins of arbitrary values. We will not demonstrate it, but give directly the result for two spins of magnitudes (maximum spin) $s_1$ and $s_2$. The possible total spins $s$ of their compound are all the values from $|s_1-s_2|$ to $s_1+s_2$ by integer steps, and the quantum states that can be taken are:
$$|sm\rangle=\sum_{m_1+m_2=m}C_{m_1m_2m}^{s_1s_2s}|s_1m_1\rangle|s_2m_2\rangle\label{eq:firstCGeq}$$
where the $C_{m_1m_2m}^{s_1s_2s}$ numbers are the so-called Clebsch-Gordan coefficients, which tabulations give one of the most bewildering images of mathematical complexity:
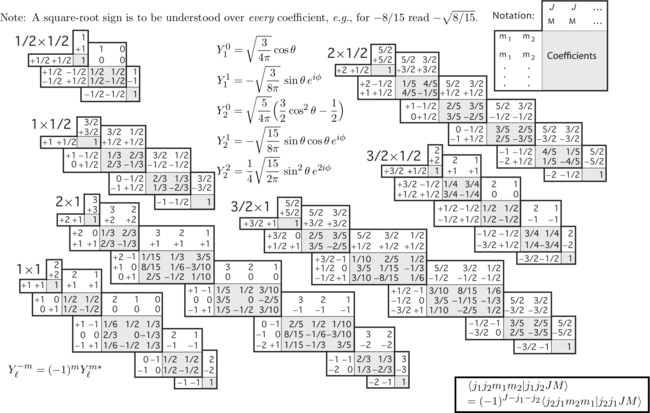
It is a lot of fun to play with these tables, that are compiled for instance by the Particle Data Group, which references everything that is known about elementary particles. In practice, there is seldom a need for them, but if you do need them, then it is merely to remember their peculiar conventions. The basic principle is as follows: the coefficients $C_{m_1m_2m}^{s_1s_2s}$ are probability amplitudes, so their modulus square are probabilities and the sum must be one. In the table, a square root is understood over all coefficients. The minus sign, if present, goes outside the square root. Equation \eqref{eq:firstCGeq} states that if you have two particles, of spins $s_1$ and $s_2$ whose total spin is $s$ (remember that it can be anything between $|s_1-s_2|$ to $s_1+s_2$) and the $z$-projection of the total is $m$, then the probability that the $s$-projections of the components are $m_1$ and $m_2$ is $|C_{m_1m_2m}^{s_1s_2s}|^2$.
This can also be inverted as follows:
$$|s_1m_1\rangle|s_2 m_2\rangle=\sum_sC_{m_1m_2m}^{s_1s_2s}|sm\rangle$$
meaning this time that two spins $s_1$ and $s_2$ which have $m_1$ and $m_2$ respective $z$-projection will result in a compound spin whose total $z$-projection is $m=m_1+m_2$ but the total spin can be $s$, with probability $|C_{m_1m_2m}^{s_1s_2s}|^2$.
References
- Particle Data Group.
- There is apparently a phobia of "tensor products". If you suffer from this, the following links may help you:
- The Tensor Product, Demystified
- How to Conquer Tensorphobia (with a quote from a Stanford professor according to whom "People run in terror from the $\otimes$ symbol".)
- How to lose your fear of tensor products