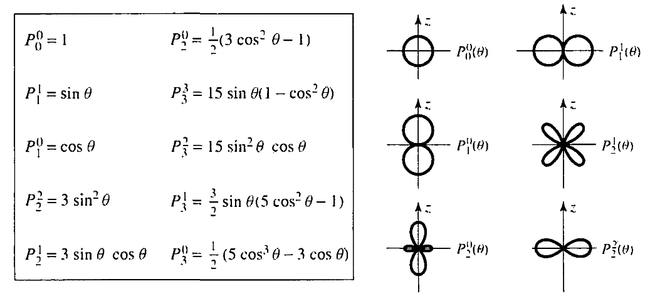Schrödinger equation in polar coordinates
(Part of the Wolverhampton Lectures of Physics's Quantum Physics Course)
In three dimensions, Schrödinger's equation is for a wavefunction of four variables, $\vec r=(x,y,z)^T$ and $t$. The momentum operator also becomes a vector:
$$\vec p\rightarrow-i\hbar\nabla\,.$$
Note that the 1D case with which we are familiar is, of course, a particular case (we remind that $\nabla=(\partial_x,\partial_y,\partial_z)^T$). For problems with symmetries, this can be brought back to a problem of smaller dimensions. For instance, we will see later how a particle in a square 2D box is really a problem of two particles in a 1D box, only with some care with the interpretation (wavefunctions need not be symmetrized for a one 2D-particle but they need to for indistinguishable two 1D-particles). Similarly, we would solve the problem of one particle in a cubic 3D box as three (unsymmetrized) 1D-particles.
We will now turn to another important case of symmetry, namely, polar symmetry, when the potential only depends on the distance to some origin. This is an important case in Physics and we will study at length the case of the Coulomb potential, $V=-(e/4\pi\epsilon_0)(1/r)$. In such a case, the wavefunction is best expressed as a function of the three polar coordinates:
$${\Psi(r,\theta,\phi)}\,.$$
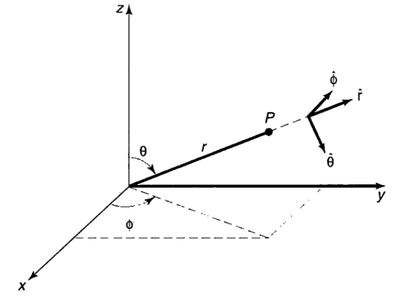
We can still apply the separation of variables, which takes the form
$$\Psi(r,\theta,\phi)=R(r)Y(\theta,\phi)\,$$
We will also break $Y(\theta,\phi)$ as $\Theta(\theta)\Phi(\phi)$ but once this is solved, this is better kept together in one single $Y$ function (the notation is standard).
The normalization of the wavefunction leads to
$$\int|\Psi|^2r^2\sin\theta drd\theta d\phi=\int|R|^2r^2dr\int|Y|^2\sin\theta d\theta d\phi=1$$
and this can also be split into the respective variables:
\begin{align}
&\int_0^\infty|R|^2r^2dr=1\,,\\
&\int_0^{2\pi}\int_0^\pi|Y|^2\sin\theta\,d\theta d\phi=1\,.
\end{align}
To write Schrödinger's (time-independent) equation $(-\hbar^2/(2m))\nabla^2\Psi+V\Psi=E\Psi$ in polar form, we need to express the Laplacian $\nabla^2$ in terms of $r, \theta, \phi$ coordinates. This reads:
$$\nabla^2={\displaystyle {1 \over r^{2}}{\partial \over \partial r}\!\left(r^{2}{\partial \over \partial r}\right)\!+\!{1 \over r^{2}\!\sin \theta }{\partial \over \partial \theta }\!\left(\sin \theta {\partial \over \partial \theta }\right)\!+\!{1 \over r^{2}\!\sin ^{2}\theta }{\partial ^{2} \over \partial \varphi ^{2}}}$$
Substituting ${\Psi(r,\theta,\phi)=R(r)Y(\theta,\phi)}$ into this equation, dividing by $YR$ and multiplying by $-2mr^2/\hbar^2$ we arrive to:
\begin{align} \left\{{1\over R}{d\over dr}\left(r^2{dR\over dr}\right)-{2mr^2\over\hbar^2}[V(r)-E]\right\} +{1\over Y} \left\{{1\over\sin\theta}{\partial\over\partial\theta}\left(\sin\theta{\partial Y\over\partial\theta}\right)+{1\over\sin^2\theta}{\partial^2Y\over\partial\phi^2}\right\} =0 \end{align}
that is, we have been able to bring all radial ($r$) variables in one term (left bracket) and all angular variables ($\theta, \phi$) in another (right). This means that, by the separation of variables, both terms must be independently equal, to the same constant, which, in this case, we will write in the form $l(l+1)$:
\begin{align} {1\over R}{d\over dr}\left(r^2{dR\over dr}\right)-{2mr^2\over\hbar^2}[V(r)-E]&=l(l+1)\label{eq:radialeq}\\ {1\over Y} \left\{{1\over\sin\theta}{\partial\over\partial\theta}\left(\sin\theta{\partial Y\over\partial\theta}\right)+{1\over\sin^2\theta}{\partial^2Y\over\partial\phi^2}\right\} &=-l(l+1)\,.\label{eq:angulareq} \end{align}
The variable $l(l+1)$ that separates the two equations is, in principle, any complex number, but it so happens, as we shall see now, that it has to be a product of two consecutive positive integers, hence the notation, which is thus, so far, no loss of generality.
Now we have to solve the two equations. One does not depend on the potential, and thus always have the same solutions for all spherically symmetric potentials. We therefore solve it first.
The Angular Equation
The separation of variables broke Schrödinger's equation in two pieces, of which one is Eq. \eqref{eq:angulareq}. We now further separate variables:
$$Y(\theta,\phi)=\Theta(\theta)\Phi(\phi)$$
which, plugged in the above equation and dividing by $\Theta\Phi$ leads us to another set of two equations, which introduces another variable (for the separation), that we call $m$:
\begin{align} {1\over\Theta}\left[\sin\theta{d\over d\theta}\left(\sin\theta{d\Theta\over d\theta}\right)\right]+l(l+1)\sin^2\theta&=m^2\\ {1\over\Phi}{d^2\Phi\over d\phi^2}&=-m^2 \end{align}
- The equation for $\Phi$ is easy:
\begin{align} {d^2\Phi\over d\phi^2}&=-m^2\Phi\Rightarrow\Phi(\phi)=e^{im\phi} \end{align}
The equation is second-order so the general solution is $Ae^{im\phi}+Be^{-im\phi}$ but we do not need to worry about the constant since this will be absorbed by the normalization later on, and the two signs can be taken into account by allowing to be positive and negative, which will indeed be the case. In fact, remembering that $\phi$ is an angle, we must have:
$$\Phi(\phi+2\pi)=\Phi(\phi)$$
therefore, $e^{im(\phi+2\pi)}=e^{im\phi}$ so that, simplifying, $e^{2im\phi}=1$. This means that $m$ must be an integer:
$$\boxed{m=0,\pm1, \pm2, \ldots}$$
- The $\Theta$ equation is not so straightforward:
$${1\over\Theta}\left[\sin\theta{d\over d\theta}\left(\sin\theta{d\Theta\over d\theta}\right)\right]+l(l+1)\sin^2\theta=m^2$$
We give the solution directly and let you check it (cf. tutorial):
$$\Theta(\theta)=AP_l^m(\cos\theta)$$
with $A$ a constant and where $P_l^m$ is the associated Legendre function, which is defined as:
$$P_l^m(x)\equiv(1-x^2)^{|m|/2}\left({d\over dx}\right)^{|m|}P_l(x)$$
in terms of the Legendre polynomial $P_l$, where $l$ is a non-negative integer. There are various (equivalent) definitions for the Legendre polynomials. One which is convenient is Rodrigues formula:
$$P_l(x)={1\over 2^ll!}\left({d\over dx}\right)^l(x^2-1)^l\,.$$
One can check that:
\begin{align}
P_0(x)&=1\\
P_1(x)&=x\\
P_2(x)&={1\over2}(3x^2-1)
\end{align}
and that in general $P_l$ is a $l$-th order polynomial. So coming back to the associated Legendre functions, we can see that $-l\le m\le l$ since $m$ can be negative (the result is the same as for positive $m$) and further derivatives beyond $l$ cancel the function.
The structure of the angular solution is thus in terms of two integers, $l$ and $m$, such that
$$\boxed{\begin{gather} l\in\mathbb{N}\\ -l\le m\le l \end{gather}}$$
i.e.,
$$l=0, 1, 2, 3, \ldots$$
and for each $l$, we have $2l+1$ possible values of $m$:
$$m=-l, -l+1, -l+2, \cdots, -1, 0, 1, \cdots, l-2, l-1, l$$
We find, e.g., for $l=2$:
$$\begin{align}
P_2^0(x)&={1\over2}(3x^2-1)\\
P_2^1(x)&=3x\sqrt{1-x^2}\\
P_2^2(x)&=3(1-x^2)
\end{align}$$
There are square roots but since in the original formula this is in terms of trigonometric functions, we find finally that the $\Theta(\theta)=P_l^m(\cos\theta)$ functions are simply polynomials of sines and cosines:
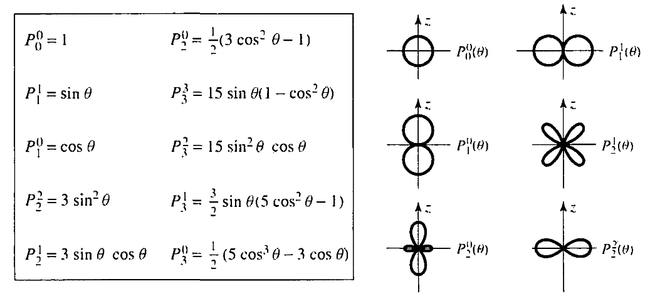
Putting this back together with the $\phi$ dependence and normalizing, we find:
$$\boxed{\displaystyle Y_l^m(\theta,\phi)=\epsilon\sqrt{{2l+1\over4\pi}{(l-|m|)!\over(l+|m|)!}} e^{im\phi}P_l^m(\cos\theta)}$$
where $\epsilon=(-1)^m$ for $m>0$ and $\epsilon=1$ for $m\le 0$. These are also orthogonal (and thus orthonormal):
$$\displaystyle\int_0^{2\pi}\int_0^\pi Y_l^m(\theta,\phi)^*Y_{\lambda}^\mu(\theta,\phi)\sin(\theta)d\theta d\phi=\delta_{l,\lambda}\delta_{m,\mu}$$
These are some particular cases for the smallest quantum numbers: