Spin ${1\over2}$

(Part of the Wolverhampton Lectures of Physics's Quantum Physics Course) $\newcommand{\updownarrows}{\mathbin\uparrow\hspace{-.3em}\downarrow}$

The spin 1/2—with two possible states $|\downarrow\rangle$ and $|\uparrow\rangle$—is so important that we already largely devoted much of the previous lecture to it. Its importance is due to several factors: first, it is the most occurring type of spin, being that of the electron, proton, neutron, etc., also being for this reason the first type of quantum spin that was discovered. Second, although the other important particle, the photon, has spin~1 by an ironic twist due to relativity, it can only have two projections of spin and is thus, effectively, a spin-1/2 object, in which case this describes polarization, that is also of central importance. Third, a spin 1/2 is the simplest case (besides the trivial spin-0 that reads more like a no-spin), and not only the simplest case of spin, but the simplest case of a quantum system, describing, in particular, a two-level system. The term pseudo-spin is sometimes encountered to refer to a two-level system that is not a magnetic spin but which follows the same algebra. A more general term for a two-level system is qubit (for "quantum bit") in which case the notation is $|0\rangle$ (say for spin up) and $|1\rangle$ (spin down). Being the simplest possible quantum system, it will be useful, and interesting, to go into the details of the measurement problem and revisit the axioms of quantum mechanics on this very particular case.

Since $|\uparrow\rangle$ and $|\downarrow\rangle$ provide a basis, the most general state of spin for an electron can be written as:

$$ |\psi\rangle=\alpha|\uparrow\rangle+\beta|\downarrow\rangle $$

with $\alpha$ and $\beta$ two complex numbers such that $|\alpha|^2+|\beta|^2=1$. One can now appreciate better that the choice of the $z$ axis was arbitrary, in the sense that the choice of a basis is a convenience that brings no loss of generality. We will indeed see that all other states can be indeed written in this way.

The axioms of quantum mechanics tell us that to measure the $z$-projection of the spin of this electron, we must invoke the corresponding observable $S_z$. Since it has eigenstates $|\uparrow\rangle$ and $|\downarrow\rangle$, we will collapse the state $|\psi\rangle$ in one of these states. This will happen with respective probabilities $|\alpha|^2$ and $|\beta|^2$. The value of spin that we measure is the corresponding eigenvalue, so if the state collapse to $|\uparrow\rangle$, we will measure $+\hbar/2$ and if it collapses to $|\downarrow\rangle$, we will measure $-\hbar/2$.

After this measurement, since the state has collapsed, say, to $|\uparrow\rangle$, and we if measure $S_z$ again, since we are now in an eigenstate of $S_z$ already, we will measure, this time for sure, $+\hbar/2$, and the state remains in the same one (or it can be seen as collapsing again on itself).

Let us now say that we want to measure the $x$-projection instead, i.e., we invoke $S_x$. What measurement will we make from the state $|\uparrow$ in which our spin currently finds itself? From the axioms again, it will be one eigenstate of $S_x$ and we will measure the corresponding eigenvalue. So we need to find the eigenstates and eigenvalues of $S_x$. This is easily done (for a $2\times2$ matrix). Since

$$S_x={\hbar\over2}\begin{pmatrix}0&1\\1&0\end{pmatrix}\,$$

the eigenvalues are found as the solution of the characteristic equation $\det(S_x-\lambda\mathbb{1})=0$, i.e.,

$$\begin{vmatrix}-\lambda & \hbar/2\\\hbar/2 & -\lambda\end{vmatrix}=0$$

i.e., $\lambda^2-\hbar^2/4=0$ with roots $\pm\hbar/2$. Therefore, $S_x$ has the same eigenvalues as $S_z$: it has the same possible projections on its axis of the angular momentum, which makes sense, remember that we chose the $z$-axis as a convention, it has nothing special, other axes should behave similarly. A spin 1/2 particle can project its spin into half a quantum of angular momentum, $+$ or $-$ depending on the sense of rotation. Not more (obviously), not less (interestingly). Let us precise the last sentence, .

We now find the eigenstates of $S_x$, which we can, pictorially, denote as $|\leftrightarrows\rangle$ (we group the arrows to mean either, or both, $|\leftarrow\rangle$ with spin $-\hbar/2$ on the $x$ axis, and $|\rightarrow\rangle$ with spin $+\hbar/2$). By "finding" we mean expressing them in terms of our initial $|\updownarrows\rangle$ (same convention here) that define the canonical basis, i.e., in column form:

$$|0\rangle=\begin{pmatrix}1\\0\end{pmatrix}\,,\quad\text{and}\quad|1\rangle=\begin{pmatrix}0\\1\end{pmatrix}\,.$$

Therefore, we are looking for the vectors $|\leftrightarrows\rangle=\left(\begin{smallmatrix}a\\b\end{smallmatrix}\right)$ which satisfy, by definition:

$$ \begin{align} S_x|\rightarrow\rangle&={\hbar\over2}|\rightarrow\rangle\\ S_x|\leftarrow\rangle&=-{\hbar\over2}|\leftarrow\rangle \end{align} $$

Given the expression for $S_x$, this gives:

$${\hbar\over2}\begin{pmatrix}b\\a\end{pmatrix}=\pm{\hbar\over2}\begin{pmatrix}a\\b\end{pmatrix}$$

with solutions

$$ \begin{align} |\rightarrow\rangle&={1\over\sqrt{2}}\begin{pmatrix}1\\1\end{pmatrix}\\ |\leftarrow\rangle&={1\over\sqrt{2}}\begin{pmatrix}1\\-1\end{pmatrix} \end{align} $$

which we have normalized. In terms of the Dirac notation:

$$\begin{align} |\rightarrow\rangle&={1\over\sqrt{2}}\left(|\uparrow\rangle+|\downarrow\rangle\right)\\ |\leftarrow\rangle&={1\over\sqrt{2}}\left(|\uparrow\rangle-|\downarrow\rangle\right) \end{align}$$

and vice-versa:

$$\begin{align} |\uparrow\rangle&={1\over\sqrt{2}}\left(|\leftarrow\rangle+|\rightarrow\rangle\right)\\ |\downarrow\rangle&={1\over\sqrt{2}}\left(|\leftarrow\rangle-|\rightarrow\rangle\right) \end{align}\,.$$

We now have the answer to our earlier question, from the first line, if the electron is in the spin state $|\uparrow\rangle$, then in the $x$-basis, it is in the state ${1\over\sqrt{2}}\left(|\leftarrow\rangle+|\rightarrow\rangle\right)$, meaning that upon measurement of its component on the $x$ axis, we will find it in either the $+$ or $-$ projection with the same probability ($|1/\sqrt{2}|^2=50\%$).

It is worth stating this again. Knowing perfectly the $z$-component, we find that the $x$-component is therefore completely randomized. We have no knowledge whatsoever on its possible projection: the state will collapse with the same probability either left or right on the $x$ axis. We let you study in the tutorial what happens with the other component (y) and practice your understanding, which will be the basis for our first applications of quantum information processing.

The same of course occurs for the $y$ axis, and we let you check that in this case, the eigenstates (with eigenvalues $\pm\hbar/2$) are

$$\begin{align} |\nearrow\rangle&={1\over\sqrt{2}}\begin{pmatrix}1\\i\end{pmatrix}={1\over\sqrt{2}}\left(|\uparrow\rangle+i|\downarrow\rangle\right)\\ |\swarrow\rangle&={1\over\sqrt{2}}\begin{pmatrix}1\\-i\end{pmatrix}={1\over\sqrt{2}}\left(|\uparrow\rangle-i|\downarrow\rangle\right) \end{align}\,.$$

In general, given the state $|\psi\rangle$, the probability to find it in the state $|\phi\rangle$ is found by the scalar (braket) product $|\langle\phi|\psi\rangle|^2$.

Such a peculiar phenomenology was demonstrated by Stern and Gerlach, by passing silver atoms through a spatially-varying magnetic field and then detecting them on a screen. This projected the atoms on two positions, as opposed to a continuous distribution, thereby demonstrating quantization of the spin.

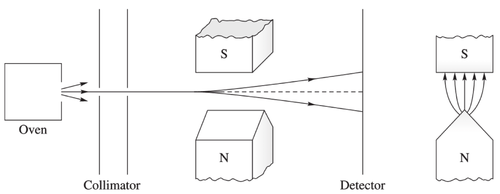
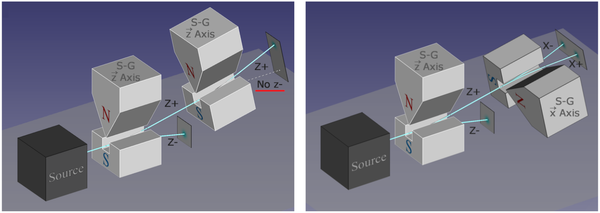
More surprisingly, by cascading their apparatuses at different angles, they observed the phenomenology of collapses and either removing the indeterminacy or, on the opposite, randomizing it depending on their choice of angle (i.e., basis).

A related effect can be demonstrated with the polarization of light [1].

One is not bound to the Cartesian axes either. Would we want to the spin projected onto an axis specified by the angles $\theta$ and $\phi$ in spherical coordinates, we would turn to:

$$\begin{align} |\chi_{+}\rangle&={\begin{pmatrix}\cos(\theta /2)\\e^{i\varphi }\sin(\theta /2)\\\end{pmatrix}}\\ |\chi _{-}\rangle&={\begin{pmatrix}\sin(\theta /2)\\-e^{i\varphi }\cos(\theta /2)\\\end{pmatrix}} \end{align}$$

which are the $\pm\hbar/2$ states along this particular axis, thereby providing an interpretation to the general superposition of the up/down (on the $z$ axis) states of spin: this corresponds to a particular axis for the projection of the spin. The collection of all states can thus be seen to span a sphere, known as the Bloch sphere, to which we will come back (in Modern Physics) when studying the technological potential for such bizarre properties. In particular, the absolute knowledge of the result when knowing the good basis and, in stark contrast, the absence of any information when using a perpendicular basis, allows to share a secret key which is the major problem of cryptography. This is done first by sending qubits to a receiver who measures them in a basis that he randomly selects for each qubit, storing the result. Afterwards, a classical, open communication of which basis had been used to encode the qubits can be shared. Lucky coincidences can be retained to provide data, the rest is just noise. The data is secret because if someone had measured in between, they would have collapsed the wavefunction and destroyed the information. This great idea, from Charles Bennett and Gilles Brassard is known as the BB84 (they proposed it in 1984) protocol, and is an example of a fundamentally secure quantum protocol. You can take it as an outstanding exercise to work out the details and check that it works, or you can wait for next year to see how this, and many other mind-boggling technologocical prowesses, can be implemented with qubits, giving rise to a new (and modern) field of quantum information processing.

References

• Stern and Gerlach: How a Bad Cigar Helped Reorient Atomic Physics.
• The Stern–Gerlach experiment at 100.
• Translation of "Der experimentelle Nachweis der Richtungsquantelung im Magnetfeld" by Stern and Gerlach, and how the translation happened on twitter.