The Radial Equation

(Part of the Wolverhampton Lectures of Physics's Quantum Physics Course)

We now turn to the radial part, which, in contrast, depends on the potential $V$, so it will have to be solved for every problem:

$${d\over dr}\left(r^2{dR\over dr}\right)-{2mr^2\over\hbar^2}[V(r)-E]R=l(l+1)R$$

To solve this equation we make a change of variable:

$$u(r)=rR(r)\,.$$

This new variable has this interesting property that the equation for $u$ becomes a 1D Schrödinger equation:

$$-{\hbar^2\over 2m}{d^2u\over dr^2}+\left[V+{\hbar^2\over2m}{l(l+1)\over r^2}\right]u=Eu$$

with the (1D) potential $V(r)+{\hbar^2\over2m}{l(l+1)\over r^2}$ that consists of the original potential augmented with a centrifugal term. Even the normalization condition is that of the 1D Schrödinger's equation, defined over $[0,\infty[$:

$$\int_0^\infty|u(r)|^2\,dr=1$$

To solve this equation, we need to specify the potential. We will later study in detail the case of the Hydrogen atom. For now, we solve a simpler case and the counterpart of one that is familiar: the infinite square well, but with polar symmetry. That makes a spherical hard box:

$$V(r)=\begin{cases} 0& \text{if $\ r\le a$}\\ \infty & \text{if $\ r>a$} \end{cases}$$

In which case the radial equation reduces to the centrifugal potential term to become:

$$-{\hbar^2\over 2m}{d^2u\over dr^2}+{\hbar^2\over2m}{l(l+1)\over r^2}u=Eu$$

which we write as

$${d^2 u\over dr^2}=\left[{l(l+1)\over r^2}-k^2\right]u$$

where

$$k\equiv{\sqrt{2mE}\over\hbar}$$

This is an image of the various potentials as a function of $l$. In these plots, the origin is at the center, and the potential becomes infinite at $r=a$ (so on both sides of the origin as well as, for $l\neq0$, at the origin itself):

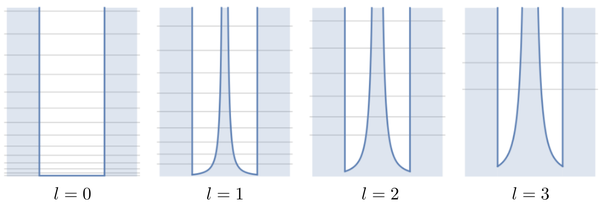
The boundary conditions is $u(a)=0$. There is only one since, unlike the 1D case, here $r>0$ (even though we plot the potential also for negative $r$, which corresponds to $\phi=\pi$). The case $l=0$ is easy:

$${d^2u\over dr^2}=-k^2u\Rightarrow u(r)=A\sin(kr)+B\cos(kr)$$

Here we must remember that $u(r)=rR(r)$ and that the physical quantity is $R(r)$, whose modulus square is the probability to find the particle at a distance $r$ (for angles specified by $\theta$ and $\phi$). Therefore, $\cos(kr)$ is not a good solution because $R$ would go like $\cos(kr)/r$ and diverge as $r\to0$, while $\sin(kr)/r\to 1$ is acceptable. Using the boundary condition on this solution, we find $\sin(ka)=0$ and thus $ka=n\pi$ for some integer $n$. This gives the quantization of the problem and a result for the energy:

$$E_{n0}={n^2\pi^2\hbar^2\over2ma^2}\,.$$

Normalizing $u(r)$ yields $A=\sqrt{2/a}$, and since $Y_0^0=1/\sqrt{4\pi}$, we have, therefore:

$$\psi_{n00}={1\over\sqrt{2\pi a}}{\sin(n\pi r/a)\over r}\,.$$

This is the first (and indeed simplest) case of $\psi_{nlm}$, that depends on three numbers. The energy, however, only depends on $n$ and $l$.

The case $l\neq 0$ has solutions:

$$u(r)=Arj_l(kr)+Brn_l(kr)$$

where $j_l$ and $n_l$ are known as the spherical Bessel and spherical Neumann functions of order $l$, respectively. They are defined as (cf. tutorial)

\begin{align} \tag{1} j_l(x)&=(-x)^l\left(\frac{1}{x}\frac{d}{dx}\right)^l\frac{\sin x}{x}\\ n_l(x)&=-(-x)^l\left(\frac{1}{x}\frac{d}{dx}\right)^l\frac{\cos x}{x} \end{align}

of which we give below some particular cases:

\begin{align} j_0&={\sin x\over x}\,, &n_0&=-{\cos x\over x}\,,\\ j_1&={\sin x\over x^2}-{\cos x\over x}\,,&n_1&=-{\cos\over x^2}-{\sin x\over x}\,,\\ j_2&=\left({3\over x^3}-{1\over x}\right)\sin x-{3\over x^2}\cos x\,,&n_2&=-\left({3\over x^3}-{1\over x}\right)\cos x-{3\over x^2}\sin x\,\dots \end{align}

Note that the case $l=0$ recovers the solutions that we already know. For the same reason as for the case $l=0$, we disqualify the cosine-like functions (Neumann) as diverging at $r=0$. There, instead, the wavefunction should actually vanish in this case since the potential becomes infinite. So the solutions are in terms of spherical Bessel functions, which have this property. The boundary condition remains the same and also yields the energy:

$$j_l(ka)=0\,.$$

Unlike the sine function, the zeros of the Bessel functions have no known closed-form expressions, and have to be computed numerically. We call them $\beta{nl}$ (i.e., $\beta_{nl}$ is the $n$th root of $j_l$, in particular, $\beta_{n0}=n\pi$), in which cases the quantization leads to:

$$k={\beta_{nl}\over a}\,.$$

As a result, the energy for the $n$, $l$ levels yields:

$$\boxed{\displaystyle E_{nl}={\hbar^2\over 2ma^2}\beta_{nl}^2}\,.$$

The wavefunctions are then:

$$\boxed{\displaystyle\psi_{nlm}(r,\theta,\phi)=A_{nl}j_l(\beta_{nl}r/a)Y_l^m(\theta,\phi)\,.}$$