Berry phase
(Part of the Wolverhampton Lectures of Physics's Quantum Physics Course)
We come back to the general problem of the time-dependent (in all senses of the term, i.e., also for the Hamiltonian) Schrödinger equation:
$$i\hbar\partial_t\psi(t)=H(t)\psi(t)\,.\label{eq:schrot}$$
The time-independent version of this time-dependent equation would involve, well, time-dependent wavefunctions (eigenstates) and energies (eigenvalues):
$$H(t)\psi_n(t)=E_n(t)\psi_n(t)\label{eq:schroit}$$
which we can still find such that they remain orthonormal:
$$\langle\psi_n(t)|\psi_m(t)\rangle=\delta_{nm}$$
at all times $t$. Formal integration of $i\hbar\partial_t\psi(t)=E(t)\psi(t)$ yields
$$\psi(t)=e^{-{i\over\hbar}\int_0^t E(\tau)\,d\tau}\psi(0)$$
so we introduce
$$\theta_n(t)\equiv-{1\over\hbar}\int_0^t E_n(\tau)\,d\tau\,.$$
In the following, we shall write the general solution in terms of the time-dependent $\psi_n$, although from the formal integration we would be entitled to do that in terms of $\psi_n(0)$ too, but in this way we will flush useful dynamics in $c_n(t)$:
$$\psi(t)=\sum_{n}c_n(t)\psi_n(t)e^{i\theta_n(t)}$$
so that, inserting it in Eq. \eqref{eq:schrot}, we find:
$$i\hbar\left(\sum_n\dot c_n\psi_n+c_n\dot\psi_n-{i\over\hbar}E_nc_n\psi_n\right)e^{i\theta_n}=\sum_n c_nE_n\psi_ne^{i\theta_n}$$
or, after cancellation:
$$\sum_n(\dot c_n\psi_n+c_n\dot\psi_n)e^{i\theta_n}=0\,.$$
Now dotting with $\langle\psi_m|$
$$\dot c_m=-\sum_n c_n\langle\psi_m|\dot\psi_n\rangle e^{i(\theta_n-\theta_m)}\,.$$
The dynamics is ruled by the overlap $\langle\psi_m|\dot\psi_n\rangle$, which we can relate through Eq. \eqref{eq:schroit} by time-derivating it:
$$\dot H\psi_n+H\dot\psi_n=\dot E_n\psi_n+E_n\dot\psi_n$$
which, again dotting with $\langle\psi_m|$, brings us to:
$$\langle\psi_m|\dot H|\psi_n\rangle+\langle\psi_m|H|\dot\psi_n\rangle=\dot E_n\delta_{mn}+E_n\langle\psi_m|\dot\psi_n\rangle$$
from which we can extract our overlap integral:
$$\langle\psi_m|\dot\psi_n\rangle(E_m-E_n)=\dot E_n\delta_{mn}-\langle\psi_m|\dot H|\psi_n\rangle$$
which, assuming for simplicity a case of non-degenerate energies and for $m\neq n$, gives us:
$$\langle\psi_m|\dot\psi_n\rangle=-{\langle\psi_m|\dot H|\psi_n\rangle\over E_m-E_n}$$
(for $m=n$, the previous expressions results to $\langle\psi_n|\dot H|\psi_n\rangle=\dot E_n$, which is true but not needed). Back to our equation for $c_m(t)$ and excluding the case $n=m$, we have, therefore:
$$\dot c_m=-c_m\langle\psi_m|\dot\psi_n\rangle+\sum_{n\neq m}c_n{\langle\psi_m|\dot H|\psi_n\rangle\over E_m-E_n} e^{i(\theta_n-\theta_m)}\,$$
and one could carry-on and try to solve this. A famous approximation of time-dependent quantum mechanics, known as the adiabatic theorem, neglects the bulky second term in the case where the time dynamics of the (time-dependent) Hamiltonian is small enough so that $\langle\psi_m|\dot H|\psi_n\rangle$ cancels and the dynamics reduces to:
$$\dot c_m=-c_m\langle\psi_m|\dot\psi_n\rangle$$
with solution
$$c_m(t)=e^{i\gamma_m(t)}c_m(0)$$
where
$$\gamma_m(t)\equiv i\int_0^t \langle\psi_m(\tau)|{\partial\over\partial\tau}\psi_m(\tau)\rangle\,d\tau$$
is called the Berry phase (also known as the geometric phase). Leaving aside this phase for a moment, which was indeed what happened historically, the previous results show that, if the "external" dynamics that changes the Hamiltonian is slow enough, one remains in the same quantum "state" that merely adapts itself to the new configuration. In particular, starting in an eigenstate $\psi_n$ of the Hamiltonian, then
$$\psi(t)=e^{i\theta_n(t)}e^{i\gamma_n(t)}\psi_n(t)$$
from which we see that the state has evolved into the corresponding $\psi_n(t)$ (which, according to our definition, changed in time to become the new eigenstate of the new Hamiltonian), up to some phase factor.
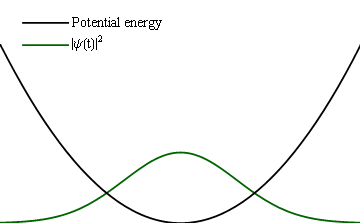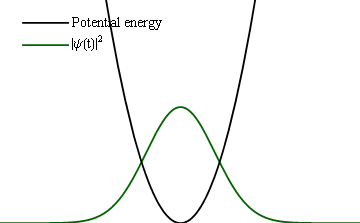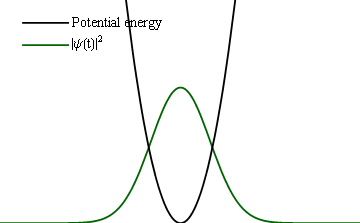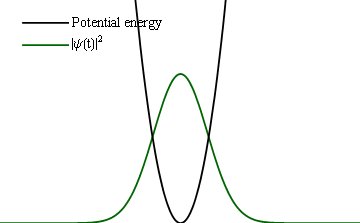
If instead of a slow change, one would make an abrupt one (at the extreme, instantaneous), then instead of such a follow-up, one would find the same (frozen) wavefunction become a new initial condition for the new Hamiltonian and thus trigger some time dynamics.
The result is thus, finally, quite intuitive, would it not be for the global phase which, anyway, is not physical or observable as removed by the modulus square. Or is it? This phase consists of two terms: the standard $\theta_n$ one that is the time-dependent counterpart of the free-energy $e^{-iE_nt/\hbar}$ which ultimately locks in the time dynamics of the various stationary states, and the newly introduced Berry phase $\gamma_n$. The latter terms originates from something changing in the Hamiltonian, say some parameter $R$ which, as we considered throughout, changes in time $R(t)$. The chain rule on the wavefunction
$${\partial\over\partial\tau}\psi_n={\partial\psi_n\over\partial R}{dR\over d\tau}$$
brings our Berry phase to:
$$\gamma_n(t)=i\int_{R_i}^{R_f}\langle\psi_n|{\partial\over\partial R}\psi_n\rangle\,dR$$
where $R_i$ and $R_f$ are the values of the parameters at the initial and final times. Would the parameter cycle in time with $R_i=R_f$, then the Berry phase would simply vanish. But let us assume now that there are several parameters that vary in time, so that the chain rule now reads:
$${\partial\over\partial\tau}\psi_n={\partial\psi_n\over\partial R_1}{dR_1\over d\tau}+\cdots+{\partial\psi_n\over\partial R_N}{dR_N\over d\tau}=(\nabla_R\psi_n)\cdot{d\mathbf{R}\over dt}$$
with $\mathbf{R}\equiv(R_1,\cdots,R_N)$. In this case:
$$\gamma_n(t)=i\int_{\mathbf{R}_i}^{\mathbf{R}_f}\langle\psi_n|\nabla_R\psi_n\rangle\cdot d\mathbf{R}$$
and if the Hamiltonian cycles back to its initial value but by making a loop in the parameter space $\mathbf{R}$ as opposed to undoing what it just did, then, the Berry phase is obtained as a contour integral:
$$\gamma_n(t)=i\oint\langle\psi_n|\nabla_R\psi_n\rangle\cdot d\mathbf{R}$$
which may be nonzero. This shows that the global phase has more meaning and substance than one might think at first. The Berry phase grew to become an important and fundamental concept in various branches of physics. It was understood by Berry himself, for instance, how the Aharonov–Bohm effect whereby a zero magnetic field can still affect, through its nonzero vector potential, the phase of a quantum wavefunction, was in fact a direct manifestation of the geometric phase. This is indeed observable by interfering a wavepacket that splits in two around such a solenoid (with no magnetic field outside but indeed a circulating vector potential there) and prompted a renewed interest on the nature of reality and various physical quantities, previously assumed to be mathematical objects.
References
- F. Wilczek and A. Shapere, eds. (1989). Geometric Phases in Physics. Singapore: World Scientific.