Variational Principle
(Part of the Wolverhampton Lectures of Physics's Quantum Physics Course)
So far we have solved all problems exactly. They have been chosen for that reason. We have been lucky that such problems were very useful in the first place. Something which is both useful and that can be solved exactly is called a textbook example, that is, something that everybody must know (or know of, and when needed, be able to go to the textbook and get or get back the knowledge out of it). In most cases:
- one is not able to solve exactly a problem and should resort to approximations.
- one is not able to solve exactly a problem and should resort to numerical solutions.
- one is able to solve exactly and over-simplified version of the problem, a so-called "toy-model".
The Second card is played by most people, and that is why numerical simulations are so important. Technically, this should be done by Computer Scientists, but these have usually so little understanding of Physics, and sometimes, even of Mathematics, that they seldom make a good job. They turn their computer code into a black box that spits answers, and this loses the essence of Physics which is understanding and interpreting. Therefore, even that is best left to Physicists and that is why we teach you so much computer programming.
The first card is the most important, this is the one we'll start filling up our hands with. Our ace-card will be the Variational Principle, that allows us to estimate the energy of the ground state. While this is for a specific case only, the ground-state energy turns out to be the most important one. It embeds several properties, in particular thermodynamical ones. It tells us about the stability of the system, etc. There is a great trick to estimate the ground state energy of systems for which we can't hope to compute it exactly. Since it is the smaller energy the system can take, for whatever (normalized) wavefunction $|\psi\rangle$ we care to choose, then the ground-state energy is smaller (or equal, if we chose the ground-state wavefunction) to the average Hamiltonian computed over this wavefunction:
$$E_g\le\langle\psi|H|\psi\rangle\,.$$
The important thing is that $|\psi\rangle$ does not have to be an eigenstate $|\psi_n\rangle$ of $H$, that is, it does not have to be a solution of the time-independent Schrödinger equation and could even be completely unrealistic for the system at hand. This makes the technique useful since in most cases, we do not know the exact solutions and might not even have a clue as to a good approximation. Just any wavefunction will do. We still have to prove that this statement is true because it is not completely clear that some wavefunction that is not an eigenstate, and thus would not be stationary, could not manage to achieve a lower energy, say, for some small amount of time.
The proof is actually straightforward: although we do not know their exact form, we know that the eigenstates $|\psi_n\rangle$ of $H$ exist and since $H$ is hermitian, that they form a basis of the space, so we can write any $|\psi\rangle$ as a linear superposition of them:
$$|\psi\rangle=\sum_n c_n|\psi_n\rangle\,.$$
The normalization of $|\psi\rangle$ requires
\begin{align}
\langle\psi|\psi\rangle&=\left(\sum_mc_m^*\langle\psi_m|\right)\sum_n c_n|\psi_n\rangle\\
&=\sum_m\sum_n c_m^*c_n\langle\psi_m|\psi_n\rangle\\
&=\sum_m\sum_n c_m^*c_n\delta_{mn}\\
&=\sum_n c_n^*c_n\\
&=\boxed{\sum_n |c_n|^2=1}\,.
\end{align}
At the same time:
\begin{align}
\langle H\rangle&=\left(\sum_mc_m^*\langle\psi_m|\right)H\left(\sum_n c_n|\psi_n\rangle\right)\\
&=\sum_m\sum_n c_m^*c_n\langle\psi_m|H|\psi_n\rangle\\ &=\sum_m\sum_n c_m^*c_nE_n\delta_{mn}\\ &=\sum_n |c_n|^2E_n\,, \end{align}
but since $E_n\ge E_g$ by definition of the ground state (being the smallest energy)
$$\sum_n |c_n|^2E_n\ge \sum_n |c_n|^2E_g$$
so we can bring $E_g$ outside of the sum on the right-hand side (it does not depend on $n$), and the remaining sum is 1. Therefore, we have indeed:
$$\langle\psi|H|\psi\rangle\ge E_g\,.$$
QED. This is the variational principle. The function $|\psi\rangle$ we chose is called the "trial wavefunction". In chemistry for instance, we cannot solve the electron-electron interaction, as we know, so we can use a trial wavefunction, with free parameters, and compute the average energy over this, which gives us an energy in terms of parameters, which we can tune to find the minimum. This will bring us as close as possible (with this trial wavefunction) to the ground state energy. We illustrate this with the ground state of Helium. We remind its Hamiltonian:
$$\displaystyle H_\mathrm{He}=\sum_{j=1}^2\left(-{\hbar^2\over 2m}\nabla_j^2-{1\over4\pi\epsilon_0}{2e^2\over r_j}\right)+{1\over4\pi\epsilon_0}{e^2\over|\vec r_1-\vec r_2|}$$
We can use as a trial wavefunction the eigenstates of $H_1+H_2$ (the hydrogenic sum). In this case, we are actually overlapping with another method known as perturbation theory, which we will cover in next lecture, where a first-order correction for the ground state is obtained from:
$$\displaystyle E'=\langle 100|\langle 100|{1\over4\pi\epsilon_0}{e^2\over|\vec r_1-\vec r_2|}|100\rangle|100\rangle$$
or, in coordinate space:
$$\displaystyle E'={e^2\over4\pi\epsilon_0}\int\int\psi_{100}^*(\vec r_1,\vec r_2){1\over|\vec r_1-\vec r_2|}\psi_{100}(\vec r_1,\vec r_2)\,d\vec r_1 d\vec r_2$$
and since for the hydrogen atom, $\psi_{100}(\vec r_1,\vec r_2)=(8/[\pi a_\mathrm{B}^3])e^{-2(r_1+r_2)/a_\mathrm{B}}$, we have:
$$\displaystyle E'={e^2\over4\pi\epsilon_0}\left({8\over\pi a_\mathrm{B}^3}\right)^2\int\int{e^{-4(r_1+r_2)/a_\mathrm{B}}\over|\vec r_1-\vec r_2|}\,d\vec r_1 d\vec r_2\,.$$
This integral can be calculated exactly. The result is
$$\displaystyle E'={5\over 4a_\mathrm{B}}\left({e^2\over4\pi\epsilon_0}\right)^2=-{5\over2}E_1=34\mathrm{eV}\,.$$
This is a positive energy, and brings the non-interacting-electrons energy $8E_1=-109\mathrm{eV}$ to -75eV, much closer to the experimental -78.975eV. Note that this is, this time, above the ground state energy, as should be from the variational principle, and in contrast to our first estimate -109eV which mainly consisted in throwing a big chunk of the Hamiltonian away! So we know the energy should be smaller than -75eV, while there's very little we can say about the -109eV estimate (just that, afterward, it is not so bad, and that it gives an estimate of the kinetic and binding energy as compared to electron repulsions).
As we shall confirm next lecture, the choice of the non-interacting (unperturbed) wavefunctions is central to perturbation theory, which uses previous approximations to build better ones in an iterative way. But in the variational method, we are not bound to such privileged wavefunctions. We can use any trial wavefunction we want (as long as it is normalized). So we can use for instance this more general trial wavefunction, as a function of the parameter $Z$:
$$\displaystyle \psi(\vec r_1,\vec r_2)={Z^3\over\pi a_\mathrm{B}^3}e^{-Z(r_1+r_2)/a_\mathrm{B}}$$
with $Z^3$ for normalization. That allows to shrink or broaden the wavefunction, possibly taking into account the screening of the other electron. Computing the average of over this wavefunction, we now find:
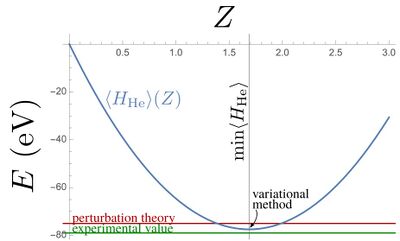
$$\langle H_\mathrm{He}\rangle=[-2Z^2+(27/4)Z]E_1$$
which has a minimum, for all values of $Z$ (remember that $E_1<0$), which hits the best approximation that this trial wavefunction can provide. The minimum is obviously found by solving for the $Z$-derivative:
$${d\over dZ}\langle H_\mathrm{He}\rangle=[-4Z+(27/4)]E_1=0$$
which gives us $Z={27\over 16}$. The energy at this value of $Z$, which is $\approx 1.69$ (that one can see as an effective screened electron charge) is:
$$\langle H_\mathrm{He}\rangle={729\over 128}E_1=-77.45\mathrm{eV}$$
which starts to get very close from the -78.975eV experimental value! One could still look for better trial wavefunctions with more parameters.
At some point, though, that would be simpler to actually numerically integrate the equation, and so the problem becomes a computational one, rather than a physics one, so we leave it to experts in those questions.