Atoms and Chemistry

(Part of the Wolverhampton Lectures of Physics's Quantum Physics Course)

We have studied in detail very simplified models of quantum mechanics, like i) the square box (infinite or not), ii) the harmonic potential or quantum oscillator, and these are already very useful to describe realistic, sophisticated systems, namely, i) quantum wells and ii) quadratures of bosonic fields, such as light, or 1st-order approximation to most potentials. We have also studied in detail complicated systems, like the hydrogen atom. In this Lecture, we will give a quick survey of how our accumulated knowledge so far serves as the building block for a large part of modern Physics, and even other disciplines, starting with chemistry.

One electron bound to one atom is the Hydrogen atom. Once we understand this one, we understand a lot of matter as a whole (energy spectra, etc.) Other atoms are merely the same thing but with $Z$ electrons instead of one, and also $Z$ protons to keep the overall structure neutral. The Hamiltonian is as follows:

$$\displaystyle H=\sum_{j=1}^Z\left(-{\hbar^2\over 2m}\nabla_j^2-{1\over4\pi\epsilon_0}{Ze^2\over r_j}\right)+{1\over2}{1\over4\pi\epsilon_0}\sum_{j\neq k}^Z{e^2\over|\vec r_j-\vec r_k|}\,.$$

At this stage, it shouldn't look a complicated object. It is complicated, but if we break it into familiar bits, then it is possible to understand what is going on. As always, it is helpful to look at a particular case of the general picture. The simplest case is of course $Z=1$ and this gives us the Hamiltonian of the hydrogen atom, which is the term in the parenthesis (without the sum). The case $Z=2$ describes the next heavier atom after Hydrogen, which is Helium. Its Hamiltonian reads:

$$\displaystyle H=\color{Red}{-{\hbar^2\over 2m}\nabla_1^2} \color{Brown}{-{1\over4\pi\epsilon_0}{2e^2\over r_1}} \color{Blue}{{-{\hbar^2\over 2m}\nabla_2^2}} \color{Teal}{-{1\over4\pi\epsilon_0}{2e^2\over r_2}} +\color{Green}{{1\over4\pi\epsilon_0}{e^2\over|\vec r_1-\vec r_2|}}$$

where we have put in colors the various terms (that's what the "breaking into bits" does):

In red and dark blue, 1st & 3rd terms, we have the kinetic energies for the two electrons.
In brown and teal, 2nd & 4 terms, we have the electron-nucleus interaction.
In green, 5th (last) term, we have the electron-electron interactions.

This Hamiltonian acts on the two-electron wavefunction:

$$\Psi(\vec r_1,\vec r_2)$$

according to Schrödinger's (time-independent) equation:

$$H\Psi=E\Psi\,.$$

So far we ignore spin, but we will put it back in due time. The subscript $i$ in the term $\nabla_i^2$ means it applies to the $i$-th variable $\vec r_i$, e.g.,

$$\nabla_1^2\Psi(\vec r_1,\vec r_2)=\left(\partial_{x_1}^2+\partial_{y_1}^2+\partial_{z_1}^2\right)\Psi(\vec r_1,\vec r_2)$$

where $\vec r_l=x_l\hat\imath+y_l\hat\jmath+z_l\hat k$ for $k=1,2$. So, if we look at the first two terms,

$$\displaystyle H_1=\color{Red}{-{\hbar^2\over 2m}\nabla_1^2} \color{Brown}{-{1\over4\pi\epsilon_0}{2e^2\over r_1}}$$

we recognize the one-electron (familiar) Schrödinger equation for Hydrogen, which we know how to solve. The only difference is that the binding of the electron to the nucleus is not to a charge $e$, as is the case for the proton of hydrogen, but to a nucleus of charge $2e$, for the two protons (and two uncharged neutrons) of Helium's nucleus. As a result, we have for the Coulomb potential $2e\times e=2e^2$ rather than the usual $e^2$. But this merely changes one parameter of the solution, not the structure of the equation. Namely, replacing one $e$ by $2e$ gives us:

A reduced Bohr radius (halved):

$$a_{\mathrm{B},\mathrm{He}}={1\over 2}{4\pi\epsilon_0\hbar^2\over me^2}={1\over 2}a_\mathrm{B}\,.$$

An increased binding energy (quadrupled):

$$E_n=-4\left[{m\over 2\hbar^2}\left({e^2\over 4\pi\epsilon_0}\right)^2\right]{1\over n^2}\,.$$

This makes physical sense: a stronger interaction makes the object smaller as the electron gets closer to the nucleus due to the stronger attraction. Although one would assume that atoms with more electrons grow in size, as we will see is indeed the case, for such "hydrogenic" atoms with only one electron, the wavefunctions are indeed more tightly packed onto the nucleus, but otherwise retain the same shape, in particular, they have the same classification: $\psi_{nlm}(\vec r)$.

The same happens for the other electron, described by the second part in the Hamiltonian, in blueish colors:

$$H_2= \textcolor{Blue}{{-{\hbar^2\over 2m}\nabla_2^2}} \textcolor{Teal}{-{1\over4\pi\epsilon_0}{2e^2\over r_2}}$$

with the same Hydrogenic equation, but for the other variable. Note in particular how the mass $m$ is the same, since all electrons have the same mass.

What makes Helium very different from what we already know is the following new bit, in green, that connects the two electrons:

$$\color{Green}{{1\over4\pi\epsilon_0}{e^2\over|\vec r_1-\vec r_2|}}\,.$$

This "interaction" term is the complicated one, which in most cases where such a direct interaction apperas, makes the system nontrivial (in the sense of "not as easy as something that can be solved exactly, like Hydrogen"). Here this describes electron-electron repulsion. Since the whereabouts of one affect the others, the problem cannot be separated. It has to be dealt with as a whole. Note how it depends on the distance between the two electrons $|\vec r_1-\vec r_2|$.

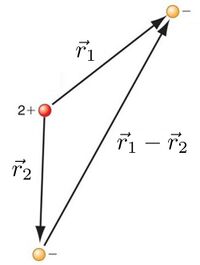
Given the might of our technical skills for solving the previous cases, this seems a fairly modest complication. But it turns out that, instead, this problem already cannot be solved exactly. Not only we don't know the solution in closed-form: there isn't any. This is a great result from Poincaré known as the three-body problem. We can solve two things, not three! Should we thus give up? No! That's where Physics enters the picture in its fullest.

In physics, we like to simplify problems. Sometimes, we oversimplify... and our theory does not work at all. But surprisingly, even in the face of very strong simplifications, one can get an extremely good description, that is, understanding, with strong approximations. For instance, we start to describe the Helium atom by simply neglecting the interaction (green) part, that is too complicated. It will also allow us to see what is due to it, and what is not.

The first (considerable) simplification, is that removing this term that connects the two electrons together, we are back to a case where they are, precisely, independent, i.e., uncorrelated, so we can write the eigenstates as:

$$\Psi(\vec r_1,\vec r_2)=\psi_{nlm}(\vec r_1)\psi_{n'l'm'}(\vec r_2)$$

We still leave spin aside for the moment and related questions (like symmetry of this two-electron wavefunction). Since neither spin nor symmetry affect the energy, we can focus on the energy spectrum. One can indeed check that the expression above is a solution to Schrödinger's (no-interacting) equation:

\begin{align} H\Psi&=(H_1+H_2)\psi_1\psi_2\\ &=H_1\psi_1\psi_2+H_2\psi_1\psi_2\\ &=(H_1\psi_1)\psi_2+\psi_1(H_2\psi_2)\\ &=E\psi_1\psi_2 \end{align}

which, dividing both sides by $\psi_1\psi_2$, yields

$$\displaystyle {H_1\psi_1\over\psi_1}+ {H_2\psi_2\over\psi_2}=E$$

and since both terms on the left only depend on their respective variables, they can be solved independently by the separation of variables: $H_i\psi_i=E_i\psi_i$ for $i=1,2$, which are the two hydrogen-like Schrödinger equations. The ground state of Helium is thus:

$$\Psi(\vec r_1,\vec r_2)=\psi_{100}(\vec r_1)\psi_{100}(\vec r_2)$$

(to be symmetrized later), or, explicitely:

$$\Psi(\vec r_1,\vec r_2)={8\over\pi a_\mathrm{B}^3}e^{-2(r_1+r_2)/a_\mathrm{B}}\,.$$

It would be difficult to sketch such a six-dimensional object... but physically, it corresponds to each electron in the same 1s cloud around the nucleus, so we cannot but imagine it like two clouds inter-penetrating each other, but not repelling (as we neglect their interactions):

Its energy is $\langle H\rangle=\langle H_1+H_2\rangle=\langle H_1\rangle+\langle H_2\rangle=8E_1$. We detail for instance the tensor-product algebra for $\langle H_1\rangle:$

$$\begin{align} \langle H_1\rangle&=\langle\Psi|H_1|\Psi\rangle\\ &=\langle\psi_1\psi_2|H_1|\psi_1\psi_2\rangle\\ &=\langle\psi_1|H_1|\psi_1\rangle\langle\psi_2|\psi_2\rangle\\ &=\langle\psi_1|H_1|\psi_1\rangle=E_1\,. \end{align}$$

Now if we compare our estimation (neglecting electrons interactions) $8E_1=8\times(-13.6)=-108.8$eV to the real value, measured in the laboratory, of -78.975eV, we see that this is fairly accurate! We are missing the effect of interactions which is positive, as it is trying to push apart (ionize, almost) the electrons, so clearly adding them would bring us to a smaller binding energy, i.e., closer to the experimental value.

Now let us include spin: electrons are fermions, and cannot be in the same state, let alone be red and blue, as we have sketched above! The total wavefunction should be antisymmetric. This is so for the ground state when we add spin:

$$\Psi(\vec r_1,\vec r_2)\chi(\vec s_1,\vec s_2)$$

where $\vec s_i$ is the spin of the electron at position $\vec r_i$ (we should avoid to say of electron $i$). So the ground state of Helium is, neglecting interactions:

$${1\over\sqrt{2}}\psi_{100}(\vec r_1)\psi_{100}(\vec r_2)(|\uparrow\downarrow\rangle-|\downarrow\uparrow\rangle)\,.$$

That is the ground state. Now, what about the excited state? One electron gets excited and jumps to a $|nlm\rangle$ state, and from this we can construct symmetric or antisymmetric spatial wavefunctions, such that the total (with spin) wavefunction is antisymmetric. This gives rise to two types of states:

parahelium (antisymmetric spin, singlet & symmetric wavefunction),
orthohelium (symmetric spin, triplet & antisymmetric wavefunction).

The ground state is therefore parahelium. The first excited state comes in both forms. Due to the exchange force bringing electrons closer together in the triplet configuration, they interact more through the green term, and so one can expect parahelium to have smaller binding energies than their corresponding orthohelium states. Indeed, 2s-para has higher energy than 1s-para (i.e., is less bound).

That is the main picture for Helium without electron-electron interactions (which we will take care of in a future lecture). We now go back to our initial Hamiltonian:

$$H=\sum_{j=1}^Z\left(-{\hbar^2\over 2m}\nabla_j^2-{1\over4\pi\epsilon_0}{Ze^2\over r_j}\right)+{1\over2}{1\over4\pi\epsilon_0}\sum_{j\neq k}^Z{e^2\over|\vec r_j-\vec r_k|}$$

Now it is clear how this works: we have hydrogenic solutions from the first sum, where each electron behaves independently from the others, and the untractable, complicated last term which correlates all the electrons together. Note the factor 1/2 due to sum counting the same term twice ($j\leftrightarrow k$). The same principles apply than for the Helium wavefunction, namely, we fill up the available states, never putting two electrons in the same state. We have shown in the Hydrogen-atom lectures that for each $n$, there are $n^2$ states $|nlm\rangle$ with $n\ge 1$ with $l$ taking values from $0$ to $n-1$, and for each $l$, we have $m$ taking values from $-l$ to $l$. In addition to that, each electron can take two projections of spin $|{1\over2},\pm{1\over2}\rangle$, so the $n$-th shell can accommodate $2n^2$ electrons.

After He, we have the $Z=3$, three-electron atom, which is Lithium. It has two electrons in the 1s states, and one electron in a $n=2$ state. The $l$-states are degenerates, but in presence of electron interactions, the $l=0$ happens to have lower energy. This can be understood qualitatively from the fact that this wavefunction is closer to the nucleus than the $l=1$ one, and therefore, is less screened by the other two electrons. This turns out to be stronger than the repulsion from the other electrons. So Lithium is $(1s)(1s)(2s)$.

The next atom, with $Z=4$, Beryllium, also puts its fourth electron in the $|200\rangle$ state (but with opposite spin). We write, for simplicity: $(1s)^2(2s)^2$.

The next atom, with Z=5, Boron, has to use the $l=1$ state, since all electronic states with $l=0$ have been taken. This carries on till $Z=10$, Neon, using the $m$ degrees of freedom (for which there are 3) and, of course, spin (that doubles them, so 6).

We thus have the following progression:

H, (1s)
He, (1s)²
Li, (He)(2s)
Be, (He)(2s)²
B, (Be)(2p)
C, (Be)(2p)²
N, (Be)(2p)³
O, (Be)(2p)⁴
F, (Be)(2p)⁵
Ne, (Be)(2p)⁶

Note that Li is very much like H in the sense that they both have one electron on their outer shell. This is what chemistry sees: the electrons on the outer shell, so Lithium and Hydrogen have much in common, in particular they are both reactive and flammable. Similarly, He and Be both feature closed outer $p$-shell, which makes them very stable.

Since at this point, the $n=2$ shell is filled, the next atoms, Na, Mg, etc., go with the $n=3$ shell:

closing the 3rd $p$ shell with the third noble atom, Argon, and you'd guess from this systematic filling that the next atom, $Z=19$, Potassium, K, would go (Ar)(3d), using the $l=2$ degree of freedom in the $n=3$ shell. But no, here the electron-electron interactions, which we have neglected up to now with no qualitative consequences, but that were piling up increasingly large corrections, enter and break the picture. It still had to wait until we reach Potassium, though: our basic, non-interacting picture is correct for the first 18 atoms! But indeed, past this point, electron interactions make the $|400\rangle$ states lower-energetic than the $|320\rangle$ ones, contrary to what the non-interacting theory says, so we first have to fill the $s$ shell

before we can go back to filling-up the $l=2$ states of the $n=3$ shell, starting with Scandium:

Alternatively, to keep track of how electrons get redistributed, we can keep Argon as the common structure:

Then, past Vanadium, one gets additional scrambling of the filling up with a return to one electron on the outer shell for Chromium:

etc. This is what gives the periodic table of elements its peculiar look, with holes, and a succession of 2 elements (1st line), 8 (2nd line), 8 (3rd line, here the missing 10 elements are distributed below), 18 (4th, missing 14 elements also distributed below, etc.) This is due to electron-electron interactions disrupting the onion-type of filling shells. Here is a zoom on the cases we have worked out in detail:

And here is a snapshot of the complete Mendeleev table:

If you are passionate about the details of this structure, and want to devote your life to it, you become a chemist. As we're physicists and not chemists, we will leave it at this stage for now. But you get the big picture!

Table of Contents

Quantum Physics