Perturbation theory

(Part of the Wolverhampton Lectures of Physics's Quantum Physics Course)

The second card in our hand of tricks to approximate solutions (first being the variational principle of the previous Lecture) is arbitrarily powerful as well as extremely general. It is almost the essence of Physics. It consists in seeing a complicated problem, that is, a complicated Hamiltonian $H$ as the sum of a simple and a complicated part:

$$H=H^{(0)}+H'\,.$$

We need not go very far to give examples of this: we have already seen an example in the previous Lectures, namely, atoms, where $H^{(0)}$ was $\sum H_i$ the single-electron hydrogenic wavefunctions and $H'$ was the ${1\over2}\sum_{j\neq j}$ the electron-electron interactions. Note that by simple we therefore do not mean "trivial" in the sense of "very easy". The hydrogen atom Hamiltonian is certainly not "easy". But it can be solved exactly, so it is simple in the sense that it yields to human's genius. Things that are hard cannot be solved (either because we're not genius enough, or, in most cases, because it is simply impossible, such as the 3-body problem).

The idea of perturbation theory is to reduce a problem to its simplest possible essence and add to this basic picture several orders of complications, of increasing complexity, that get closer and closer to the true object. You have already seen the idea many times, of course, especially from its mathematical foundation which is the series expansion, e.g.,

$$\displaystyle\sin(x)=x-{x^3\over 6}+{x^5\over 120}+\cdots\tag{1}$$

which asserts that to leading order, or a first approximation, the sine is simply the identity. This is outrageous regarding the function as a whole, since so many of its central features are lost, such as its periodicity, the fact that it is bounded, its infinite number of zeros, its beautiful behavior with respect to iterated derivatives, etc. But often, this is indeed a good, if not even sufficient, approximation. In optics, for instance, this gives rise to the paraxial approximation, which captures pretty much all the physics of optical devices (mirrors, lenses, the eye, cameras, etc.)

Then comes the "perturbation", which corrects, or refines, the behavior of the function, namely, here, a cubic departure from linearity, showing how the function flexes down and ultimately even changes direction (going downward). Surprisingly, such a first-order correction typically gets very close to, at least a qualitative behavior of the function. Here is a physicist's sine function:

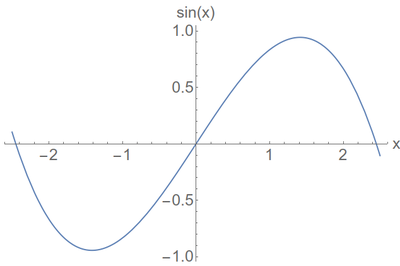
If you show this to someone at glance and they would not pay much attention to the labels, and if you'd ask them which function that is, then it is likely they would identify it as the sine. It is, instead, the first two-leading terms from \eqref (1). The zeros are thus at $\pm\sqrt{6}\approx\pm2.45$ instead of $\pm\pi$ and the coming-back towards the axis is too steep for a sine, as compared to the ascent which is harmonically beautiful, and it also fails to hit 1, so if we are after the details, this is clearly not a sine, but a rough idea (linear) and a small correction brings us to a surprisingly eerie lookalike.

Unfortunately, the higher orders, although improving, are typically not equally successful, and the convergence to the exact solution gets considerably slower. The next order in fact loses some of its qualitative charms and one has to go to fourth order to recover some good-looking, almost impeccable version on the central period, but by this time we're not in Physics anymore but some other field of science: computer science, engineering, etc.

Back to quantum mechanics, the perturbation method works when we plug-in a small term $H'$ (the perturbation) to some simple (or at least, do-able) bulk Hamiltonian $H^{(0)}$ that captures the gist of the phenomenon. The mathematical justification relies on the small numerical departure brought by $H'$ to $H^{(0)}$. To make this point clear, regardless of the exact magnitude of the perturbation, we can bring a scaling coefficient $\lambda$ in front that we can tune to satisfy more or less the requirement:

$$H=H^{(0)}+\lambda H'$$

where we should have, in principle, $\lambda\ll 1$ or even $\lambda\rightarrow 0$. Even when this is not exactly the case, as in Helium where the electron-electron interaction was bringing ~27eV to the main Hamiltonian 109eV, so a sizable fraction, it was still the smaller part. We will see that, like for our sine function, even when the "perturbation" is large, it gives surprisingly good results.

We therefore have at our disposition the set of solution for $H^{(0)}$, i.e., the $\psi_n^{(0)}$ and associated $E_n^{(0)}$ such that

$$H^{(0)}\psi_n^{(0)}=E_n^{(0)}\psi_n^{(0)}\,.$$

These solution have been chosen such as to form an orthonormal basis of the vector space of all solutions, i.e.,

$$\langle\psi_n^{(0)}|\psi_m^{(0)}\rangle=\delta_{nm}\,.$$

Our goal of course is not $H^{(0)}$, the "easy" problem, but $H$, the tough one. That is, we want to find $\psi_n$ and $E_n$ that are solution of:

$$H\psi_n=E_n\psi_n\,.$$

If $\lambda$ is a small parameter, it invites to make a series expansion of the sought solutions in terms of powers of $\lambda$:

\begin{align} \psi_n&=\psi_n^{(0)}+\lambda\psi_n^{(1)}+\lambda^{2}\psi_n^{(2)}+\cdots\\ E_n&=E_n^{(0)}+\lambda E_n^{(1)}+\lambda^2E_n^{(2)}+\cdots\\ \end{align}

where the terms labeled ${}^{(1)}$ are first-order corrections, terms labeled ${}^{(2)}$ are second-order corrections, etc. At this stage we just do what Maths makes it easy to do, explore the automatic consequences of our fooling around with expressions. So we just plug these into Schrödinger's equation $H\psi_n=E_n\psi_n$. This gives:

$$(H^{(0)}+\lambda H')(\psi_n^0+\lambda\psi_n^1+\lambda^2\psi_n^2+\cdots)=(E_n^0+\lambda E_n^1+\lambda^2E_n^2+\cdots)(\psi_n^0+\lambda\psi_n^1+\lambda^2\psi_n^2+\cdots)$$

Let us collect the like-powers of $\lambda$:

\begin{multline} H^{(0)}\psi_n^{(0)}+\lambda(H^{(0)}\psi_n^{(1)}+H'\psi_n^{(0)})+\lambda^2(H^{(0)}\psi_n^{(2)}+H'\psi_n^{(1)})+\cdots\\ =E_n^{(0)}\psi_n^{(0)}+\lambda(E_n^{(0)}\psi_n^{(1)}+E_n^{(1)}\psi_n^{(0)})+\lambda^2(E_n^{(0)}\psi_n^{(2)}+E_n^{(1)}\psi_n^{(1)}+E_n^{(2)}\psi_n^{(0)})+\cdots \end{multline}

That looks terrible, but this is just old-good standard algebra with fancy notations (we need it not to mix the labels with powers; some people confide in context and do without the extra parenthesis).

To lowest-order in $\lambda$, or $\lambda=0$, this equation gives us back our "easy problem":

$$H^{(0)}\psi_n^{(0)}=E_n^{(0)}\psi_n^{(0)}\,.$$

Fine, we expect that. To first-order, we have already something we can work with:

$$H^{(0)}\psi_n^{(1)}+H'\psi_n^{(0)}=E_n^{(0)}\psi_n^{(1)}+E_n^{(1)}\psi_n^{(0)}\,.$$

Similarly, to second-order in $\lambda$, i.e., considering the $\lambda^2$ terms:

$$H^{(0)}\psi_n^{(2)}+H'\psi_n^{(1)}=E_n^{(0)}\psi_n^{(2)}+E_n^{(1)}\psi_n^{(1)}+E_n^{(2)}\psi_n^{(0)}\,.$$

Now we can solve these equations separately. They will provide first-order type of correction, and second-order (you can work out third-order, etc., but at this stage it becomes a problem for somebody else). The first-order case is called:

First-order perturbation theory

We will rewrite our equation with Dirac notations because we are going to take scalar products:

$$H^{(0)}|\psi_n^{(1)}\rangle+H'|\psi_n^{(0)}\rangle=E_n^{(0)}|\psi_n^{(1)}\rangle+E_n^{(1)}|\psi_n^{(0)}\rangle$$

and let us look at what happens if we dot that with $\langle\psi_n^{(0)}|$:

$$\langle{\psi^{(0)}_n}|H^{(0)}|\psi_n^{(1)}\rangle+\langle{\psi^{(0)}_n}|H'|\psi_n^{(0)}\rangle=\langle{\psi^{(0)}_n}|E_n^{(0)}|\psi_n^{(1)}\rangle+\langle{\psi^{(0)}_n}|E_n^{(1)}|\psi_n^{(0)}\rangle\,.$$

Let us compute what we can, using the definitions (of course, as always, we need to know what we are doing, i.e., understanding what these various terms are, which mainly means, processing the notation):

$$E_n^{(0)}\langle{\psi^{(0)}_n}|\psi_n^{(1)}\rangle+\langle{\psi^{(0)}_n}|H'|\psi_n^{(0)}\rangle=E_n^{(0)}\langle{\psi^{(0)}_n}|\psi_n^{(1)}\rangle+E_n^{(1)}\langle{\psi^{(0)}_n}|\psi_n^{(0)}\rangle$$

so, simplifying and re-arranging:

$$\boxed{\displaystyle E_n^{(1)}= {\langle{\psi^{(0)}_n}|H'|\psi_n^{(0)}\rangle}}$$

since $\langle{\psi^{(0)}_n}|\psi_n^{(0)}\rangle=1$ (states are normalized). Here we have the grand result (explaining the link to the variational principle from the previous lecture):

The first-order correction to the energy is the average of the unperturbed wavefunction on the perturbation Hamiltonian.

That gives us the correction to the energy. How about the correction to the wavefunction? We go back to this equation:

$$H^{(0)}|\psi_n^{(1)}\rangle+H'|\psi_n^{(0)}\rangle=E_n^{(0)}|\psi_n^{(1)}\rangle+E_n^{(1)}|\psi_n^{(0)}\rangle$$

and rewrite it for the quantity we're looking for:

$$(H^{(0)}-E_n^{(0)})|\psi_n^{(1)}\rangle=(-H'+E_n^{(1)})|\psi_n^{(0)}\rangle$$

We know everything on the right-hand side, so we have an operator-equation (that is, depending on the operator, it could be a differential equation) for $|\psi_n^{(1)}\rangle$. We can find it in terms of the $|\psi_n^{(0)}\rangle$ basis vectors:

$$|\psi_n^{(1)}\rangle=\sum_{m}c_m^{(n)}|\psi_m^{(0)}\rangle\,.$$

Note that we need two indices $c_m^{(n)}$ for the coefficients as we want all the perturbed wavefunctions and each may depend on all the unperturbed basis states. Actually, we can remove the $m=n$ case as can be seen by substitution of $|\psi_n^{(1)}\rangle$ in the above equation:

$$\displaystyle(H^{(0)}-E_n^{(0)})\sum_{m\neq n}c_m^{(n)}|\psi_m^{(0)}\rangle=(-H'+E_n^{(1)})|\psi_n^{(0)}\rangle$$

where we removed the term $c_n^{(n)}(H^{(0)}-E_n^{(0)})|\psi_n^{(0)}\rangle$ since this cancels (being the solution of Schrödinger equation for the unperturbed case). For the other terms, they become:

$$\displaystyle\sum_{m\neq n}c_m^{(n)}\displaystyle(E_m^{(0)}-E_n^{(0)})|\psi_m^{(0)}\rangle=(-H'+E_n^{(1)})|\psi_n^{(0)}\rangle\,.$$

We're after the coefficients $c_m^{(n)}$, remember. We can get them by dotting with $\langle\psi_k^{(0)}|$:

$$\displaystyle\sum_{m\neq n}c_m^{(n)}\displaystyle(E_m^{(0)}-E_n^{(0)})\langle\psi_k^{(0)}|\psi_m^{(0)}\rangle=\langle\psi_k^{(0)}|(-H'+E_n^{(1)})|\psi_n^{(0)}\rangle$$

Since $\langle\psi_k^{(0)}|\psi_m^{(0)}\rangle=\delta_{km}$, we have:

$$\displaystyle c_k^{(n)}(E_k^{(0)}-E_n^{(0)})=-\langle\psi_k^{(0)}|H'|\psi_n^{(0)}\rangle+\langle\psi_k^{(0)}|E_n^{(1)}|\psi_n^{(0)}\rangle$$

If $k=n$, the left-hand side cancels and we recover the result for the energy. Otherwise, the last term on the right-hand side cancels (by orthogonality) and we find:

$$\displaystyle c_k^{(n)}=-{\langle\psi_k^{(0)}|H'|\psi_n^{(0)}\rangle\over E_k^{(0)}-E_n^{(0)}}$$

provided that $E_k^{(0)}\neq E_n^{(0)}$, i.e., provided that the energies are not degenerate. That's often okay in 1D but is rarely a good hypothesis in problems of several dimensions. In this case, one needs a so-called "degenerate perturbation theory", which however we will leave for when you will actually need it. For now, we will content with this solution for the wavefunction:

$$\displaystyle\boxed{|\psi_n^{(1)}\rangle=\sum_{m\neq n}{\langle\psi_m^{(0)}|H'|\psi_n^{(0)}\rangle\over E_n^{(0)}-E_m^{(0)}}|\psi_m^{(0)}\rangle\,.}$$

This is not as good an approximation to the exact result as for the energy... But that's the theory. Besides, this is needed if we want to push perturbation theory to the next order:

Second-order perturbation theory

This is the same, really, just starting this time with (in Dirac notations):

$$H^{(0)}|\psi_n^{(2)}\rangle+H'|\psi_n^{(1)}\rangle=E_n^{(0)}|\psi_n^{(2)}\rangle+E_n^{(1)}|\psi_n^{(1)}\rangle+E_n^{(2)}|\psi_n^{(0)}\rangle$$

which we dot with $\langle\psi_n^{(0)}|$:

$$\langle\psi_n^{(0)}|H^{(0)}|\psi_n^{(2)}\rangle+\langle\psi_n^{(0)}|H'|\psi_n^{(1)}\rangle=\langle\psi_n^{(0)}|E_n^{(0)}|\psi_n^{(2)}\rangle+\langle\psi_n^{(0)}|E_n^{(1)}|\psi_n^{(1)}\rangle+\langle\psi_n^{(0)}|E_n^{(2)}|\psi_n^{(0)}\rangle$$

and we compute:

$$E_n^{(0)}\langle\psi_n^{(0)}|\psi_n^{(2)}\rangle+\langle\psi_n^{(0)}|H'|\psi_n^{(1)}\rangle= E_n^{(0)}\langle\psi_n^{(0)}|\psi_n^{(2)}\rangle+E_n^{(1)}\langle\psi_n^{(0)}|\psi_n^{(1)}\rangle+E_n^{(2)}$$

the term $E_n^{(0)}\langle\psi_n^{(0)}|\psi_n^{(2)}\rangle$ cancels on both sides of this equation, so we are left with:

$$E_n^{(2)}=\langle\psi_n^{(0)}|H'|\psi_n^{(1)}\rangle-E_n^{(1)}\langle\psi_n^{(0)}|\psi_n^{(1)}\rangle\,.$$

We know $|\psi_n^{(1)}\rangle$ from first-order theory, in particular, we know that it has no overlap with $|\psi_n^{(0)}\rangle$, so the rightmost term cancels. For the other one, we compute

$$\begin{align} \langle\psi_n^{(0)}|H'|\psi_n^{(1)}\rangle &=\langle\psi_n^{(0)}|H'|\sum_{m\neq n}{\langle\psi_m^{(0)}|H'|\psi_n^{(0)}\rangle\over E_m^{(0)}-E_n^{(0)}}|\psi_m^{(0)}\rangle\\ &=\sum_{m\neq n}{\langle\psi_m^{(0)}|H'|\psi_n^{(0)}\rangle\over E_m^{(0)}-E_n^{(0)}}\langle\psi_n^{(0)}|H'|\psi_m^{(0)}\rangle\\ &=\sum_{m\neq n}{\left|\langle\psi_m^{(0)}|H'|\psi_n^{(0)}\rangle\right|^2\over E_m^{(0)}-E_n^{(0)}}\\ \end{align}$$

which gives us the second-order energy correction:

$$\boxed{\displaystyle E_n^{(2)}=\sum_{m\neq n}{\left|\langle\psi_m^{(0)}|H'|\psi_n^{(0)}\rangle\right|^2\over E_m^{(0)}-E_n^{(0)}}\,.}$$

Here again, this is non-degenerate theory. The idea is the same, but this time, we get a correction of the perturbed energy by averaging the perturbation over cross-products of the unperturbed wavefunctions. The power and interest of this method will be unleashed in applications. Let us work out an easy example, namely, of a Dirac delta potential placed at the center of the infinite square box, i.e., with potential: 

$$H'=V_0\delta(x-L/2)$$

for a potential of width $L$, with stationary states

$$\displaystyle \psi_n(x)=\sqrt{2\over L}\sin({n\pi x\over L})\,.$$

Merely applying the formulas which we have obtained above, we find, to first order:

$$\begin{align} E_n^{(1)}&=\langle{\psi_n}|H'|{\psi_n}\rangle\\ &=\int\psi_n^*(x)V_0\delta(x-L/2)\psi_n(x)\,dx\\ &=V_0|\psi_n(L/2)|^2\\ &={2V_0\over L} \hbox{if $n$ is odd} \end{align}$$

and to second order:

$$\displaystyle E_n^{(2)}=\sum_{m\neq n}{\left|{2V_0\over L}\sin({n\pi\over2})\sin({m\pi\over 2})\right|^2\over{\hbar^2\pi^2\over 2m_0L^2}(n^2-m^2)}$$

so that, simplifying, since the numerator is zero unless both $n$ and $m$ are simultaneously odd, in which case it simplifies to 1:

$$\displaystyle E_n^{(2)}={8V_0^2m_0\over{\hbar^2\pi^2}}\sum_{m\neq n\atop m \mathrm{\ odd}}{1\over(n^2-m^2)} \hbox{if $n$ is odd}\,.$$

This is a funny sum to evaluate. A possible way is to decompose:

$$\displaystyle {1\over n^2-m^2}={1\over 2n}\left({1\over m+n}-{1\over m-n}\right)$$

and look for cancellations. Introspection shows that the sum is equal to $-1/(2n)^2$ in which case:

$$\displaystyle E_n^{(2)}=-{8V_0^2m_0\over{(\hbar2n\pi)^2}} \hbox{if $n$ is odd}$$

Note that it is negative, correcting downward, but to a lesser extent, the first-order approximation. We do not have the exact result, but we can now convince ourselves that we could get arbitrarily close to it, starting with:

$$E_n={\hbar^2\pi^2\over 2m_0L^2 n^2}+{2V_0\over L}-{8V_0^2m_0\over{(\hbar2n\pi)^2}}+\dots$$

for $n$ odd, otherwise, $E_n$ remains equal to its unperturbed (leading-order) value, which makes sense since the corresponding wavefunctions are zero at the point where the potential acts, and so cannot feel it.