Time-dependent Hamiltonians

(Part of the Wolverhampton Lectures of Physics's Quantum Physics Course)

So far, we have relied on the separation of space and time variables in Schrödinger's equation, so that we have been concerned, mainly, with the time-independent Schrödinger equation:

$$ H\psi=E\psi\,. $$

In this case, the stationary states $\psi_n$, which form a basis of solutions, are independent the ones from the others: if we start there, we stay there. One has to turn to a linear superposition of them to trigger some nontrivial dynamics:

$$\psi(t)=\sum_nc_n\psi_n e^{-iE_nt/\hbar}\tag{1}$$

with the (constant) $c_n$ decided by the initial condition $\psi(0)$.

The separation of variables was possible thanks to the Hamiltonian being itself time independent. In the case where the Hamiltonian is time-dependent, there are no more stationary states and most observables will consequently also acquire a time dynamics. Physics being what it is, though (bringing interpretation and meaning to the equations that describe the universe), in such cases, it turns out to be conceptually advantageous to still refer to stationary states, and assume instead that the system undergoes transitions between them. For instance, one can still imagine a ground state and an excited state, and that the time-dependent part of the Hamiltonian induces transitions between them. We then call the time-dependent part the "excitation" of what is otherwise our normal system.

This reminds the framework of perturbation theory, with something stable, big, fundamental that is refined, perturbed or affected by another term that is plugged onto it. This picture is all the more justified by the fact that time-dependent parts in nature are typically small and indeed acting as a perturbation on a stationary, big object. This is typically the case, in particular, for an electromagnetic field that drives an atom: light-matter interaction scales according to the fine structure constant $\alpha$ which is very small.

With this short introduction, we have set up the program for our lecture: bringing perturbation theory to time-dependent Hamiltonians:

$$H(t)=H_0+H'(t)\,.$$

We will focus on a two-level system, since transitions typically go from one initial state $i$ to some final one $f$ that are selected out of all those available by the driving frequency of the field: level that are out-of-resonance can just be ignored. Assuming, therefore, two stationary states of our time-independent $H_0$:

\begin{align} H_0|\psi_a\rangle&=E_a|\psi_a\rangle\\ H_0|\psi_b\rangle&=E_b|\psi_b\rangle \end{align}

The counterpart of Eq. (1) for the time-dependent Hamiltonian $H(t)$ can also be written as a linear superposition of $H_0$'s eigenstates (which still form a basis), but now with time-dependence of the probability amplitudes $c_n(t)$ in addition to that brought by the energy terms $e^{-iE_nt/\hbar}$ (with $E_n$ still time-independent as they are $\psi_n$'s corresponding eigenvalues for $H_0$, and nothing changes there):

$$\psi(t)=c_a(t)\psi_ae^{-iE_at/\hbar}+c_b(t)\psi_be^{-iE_bt/\hbar}\,.$$

Inserting this formal solution in both sides of the time-dependent Schrödinger equation $i\hbar\partial_t\psi=(H_0+H'(t))\psi$, we find:

\begin{align} i\hbar\partial_t\psi&=i\hbar\dot c_a\psi_a e^{-iE_at/\hbar}+c_aE_a\psi_ae^{-iE_at/\hbar} +i\hbar\dot c_b\psi_be^{-iE_bt/\hbar}+c_bE_b\psi_be^{-iE_bt/\hbar}\\ H(t)\psi&=c_aE_a\psi_a e^{-iE_at/\hbar}+c_bE_b\psi_b e^{-iE_bt/\hbar}+H'(t) c_a\psi_a e^{-iE_at/\hbar}+H'(t)c_b\psi_b e^{-iE_bt/\hbar} \end{align}

This is an example of a do-it-yourself calculation that looks forbidding to whoever didn't write it down themselves. There is nothing more here than trivial algebra and the product rule. Equating both lines and simplifying, we can reduce this to:

$$i\hbar\dot c_a|\psi_a\rangle e^{-iE_at/\hbar}+i\hbar\dot c_b|\psi_b\rangle e^{-iE_bt/\hbar}=H'(t) c_a|\psi_a\rangle e^{-iE_at/\hbar}+H'(t)c_b|\psi_b\rangle e^{-iE_bt/\hbar}\,.$$

$\psi_a$ and $\psi_b$ being orthonormal basis states, we can get rid of one of them by taking the scalar product with the other one. Introducing for concision the overlap integral

$$H'_{ij}\equiv\langle\psi_i|H'|\psi_j\rangle$$

for $i,j\in\{a, b\}$, we find:

$$i\hbar\dot c_a e^{-iE_at/\hbar}=c_a\langle H'\rangle_{aa} e^{-iE_at/\hbar}+c_b\langle H'\rangle_{ab} e^{-iE_bt/\hbar}$$

of, after multiplying by $-ie^{iE_at/\hbar}/\hbar$:

$$\dot c_a=-{i\over\hbar}\left[c_a\langle H'\rangle_{aa}+c_b\langle H'\rangle_{ab} e^{-i(E_b-E_a)t/\hbar}\right]\,.$$

Similarly for $c_b$:

$$\dot c_b=-{i\over\hbar}\left[c_b\langle H'\rangle_{bb}+c_a\langle H'\rangle_{ba} e^{i(E_b-E_a)t/\hbar}\right]\,.$$

Often the diagonal elements are zero, due to selection rules, and we shall focus on this case from now on. These are, therefore, the time-dependent equations for the probability amplitudes of a two-level system:

\begin{align} \dot c_a&={-i\over\hbar}H'_{ab}e^{-i\omega_0t}c_b\,,\\ \dot c_b&={-i\over\hbar}H'_{ba}e^{i\omega_0t}c_a\,, \end{align}

where we introduced the transition frequency between the two levels:

$$\hbar\omega_0\equiv E_b-E_a\,.$$

Note that, although we worked in the framework of perturbation theory, these equations are in fact exact so far. Therefore, solving them would in fact provide the exact result (remember that perturbation theory is an approximation). Since $H'$ is usually complicated, this turns out to be often impractical when not impossible. Of course, one can always recourse to numerical integration. Instead, we shall now deploy the might of perturbation theory by solving this to increasing orders of accuracy. We will also consider cases that can be solved exactly.

Starting from what we'll call the ground state (to fix ideas, but of course this is just a label):

$$c_a(0)=1\quad\text{and}\quad c_b(0)=0$$

to lowest (zeroth) order, $H'=0$ and the probability amplitudes are constant, so the system does not move: it is stationary. As expected (to lowest order).

To first order, $\dot c_a=0$ and thus the ground state still remains stationary:

$$c_a^{(1)}(t)=1\,,$$

where the superscript $(1)$ refers to the order of the dynamics.

Since we expect that $|c_a|^2+|c_b|^2=1$ at all times, does not this compel $c_b$ to also remain constant at least in amplitude? No, because we are now making approximations, so normalization can only be retained approximately, and in this case, indeed, to first-order accuracy:

$$\dot c_b={-i\over\hbar}H'_{ba}e^{i\omega_0t}\implies c_b^{(1)}(t)={-i\over\hbar}\int_0^t H'_{ba}(\tau)e^{i\omega_0\tau}d\tau\,.$$

We would have to specify the time-dependent term to delve further into the details of $c_b$'s evolution. Instead, still keeping $H'$ general, we can now use these first-order solutions as a seed for the differential equation, which will provide the 2nd-order correction:

\begin{align} \dot c_a^{(2)}={-i\over\hbar}H'_{ab}e^{-i\omega_0t}c_b^{(1)}\implies c_a^{(2)}(t)&={-i\over\hbar}\int_0^tH'_{ab}e^{-i\omega_0\tau_2}\left({-i\over\hbar}\int_0^{\tau_2} H'_{ba}(\tau_1)e^{i\omega_0\tau_1}d\tau_1\right)d\tau_2\,,\\ \dot c_b^{(2)}={-i\over\hbar}H'_{ba}e^{i\omega_0t}c_a^{(1)}\implies c_b^{(2)}(t)&={-i\over\hbar}\int_0^t H'_{ba}(\tau)e^{i\omega_0\tau}d\tau\,. \end{align}

Note that $c_b^{(2)}(t)=c_b^{(1)}(t)$ just like we had to first order with $c_a^{(1)}(t)=c_a(0)$. Indeed, we could call $c_a^{(0)}(t)\equiv c_a(0)$ as this is precisely the 0-th order approximation, the crudest one: no attempt at going further than what we already have! This would make the link even clearer: successive approximations bring corrections to every-other term of the pair.

The double integral (integral of an integral) is admittedly nasty, but remember that this is improving in accuracy, a process which often can be turned to  another layer of expertise (numerical integration, etc.) There also exist dedicated methods (diagram expansion) to keep track of such a procedure. Finally, in some cases, including of great interest, the integration can actually be performed. Regardless, we are often content to limit to the first-order result.

Let us consider for instance the important case of harmonic perturbation:

$$H'=V\cos(\omega t)$$

with the operator $V$ such that its off-diagonal elements $V_{ab}\equiv\langle\psi_a|V|\psi_b\rangle$ make $H'_{ab}=V_{ab}\cos(\omega t)$ nonzero but its diagonal elements are 0. In this case, we have:

$$\begin{align} c_a^{(1)}(t)&=1\,,\\ c_b^{(1)}(t)&={-iV_{ba}\over\hbar}\int_0^t \cos(\omega\tau)e^{i\omega_0\tau}d\tau\,. \end{align}$$

Integrating the cosine gives:

$$\displaystyle{-iV_{ba}\over\hbar}\int_0^t {e^{i\omega\tau}+e^{-i\omega\tau}\over 2}e^{i\omega_0\tau}d\tau=-{V_{ba}\over2}\left[{e^{i(\omega_0+\omega)t}-1\over\omega_0+\omega}+{e^{i(\omega_0-\omega)t}-1\over\omega_0-\omega}\right]$$

which can be further simplified by dropping the $\omega+\omega_0$ term which is greatly out of resonance, and thus not efficient to drive a transition, leaving us with the close-to-resonance case:

$$\begin{align} c_b^{(1)}(t)&\approx{V_{ba}\over2}{e^{i(\omega_0-\omega)t}-1\over\omega_0-\omega}= {V_{ba}\over2}{e^{i(\omega_0-\omega)t/2}\over\omega_0-\omega}(e^{i(\omega_0-\omega)t/2}-e^{-i(\omega_0-\omega)t/2})\\ &=-i{V_{ba}\over\hbar}{\sin[(\omega_0-\omega)t/2]\over\omega_0-\omega}e^{i(\omega_0-\omega)t/2} \end{align}$$

The probability follows by taking the modulus square:

$$\displaystyle P_{a\to b}(t)={|V_{ba}|^2\over\hbar^2}{\sin^2[(\omega_0-\omega)t/2]\over(\omega_0-\omega)^2}$$

The probability appears to oscillate. Since this is a first-order perturbation, one should however assume that this is accurate only at short times, in which case:

$$\displaystyle P_{a\to b}(t)\approx {|V_{ba}|^2\over4\hbar^2}{t^2}$$

which eventually will break down (and break down badly as it will even overcome unity). In this particular case, however, and as long as the probabilities remain small enough, the result turns out to be, at least qualitatively, exact, as we shall confirm by then solving the problem exactly: the probability oscillates and returns to 0, so there are times, periodically, when the system is sure to be found (or to be back) in the ground state.

The perturbation is thus not efficient in the sense that the more it applies, the better is the chance of it to induce the transition. Quite on the opposite, one should know where to stop. This is in fact a central feature of quantum mechanics, rooted in the Hermitian structure of the theory, that makes it reversible. If the transition can go one way, it has to be able to come back the other way. Indeed $V_{ab}=V_{ba}$ (Hermiticity), which is the reason for the oscillations. They are known as Rabi oscillations, after the scientist (Isidor) who first described them with a spin-1/2 system bathing in a magnetic field.

Rabi oscillations are a rare case of a time dynamics which can be obtained exactly, if driving with $H_{ab}'={V_{ab}\over2}e^{i\omega t}$ rather than a cosine, in which case the exact equations take the simple form:

$$\begin{align} \dot c_a&={g\over2}e^{-i\Delta t}c_b\\ \dot c_b&=-{g^*\over2}e^{i\Delta t}c_a \end{align}$$

where we introduced the so-called detuning:

$$\Delta\equiv\omega-\omega_0$$

as well as some tidied-up coupling term in the form of some coupling (complex) frequency:

$$\displaystyle g\equiv{-iV_{ab}\over\hbar}\,.$$

This can indeed be solved by substituting the 2nd equation in the derivative of the 1st:

$$\ddot c_a={g\over2}(-i\Delta)e^{-i\Delta t}c_b+{g\over2}e^{-i\Delta t}\dot c_b$$

that, rewriting in terms of $c_a$ alone, simplifies to a time-independent differential equation:

$$\displaystyle\ddot c_a=-i\Delta\dot c_a-{|g|^2\over 4}c_a$$

with characteristic polynomial:

$$\displaystyle\lambda^2+\lambda\Delta-{|g|^2\over4}=0$$

and solutions:

$$\displaystyle\lambda_\pm\equiv{-\Delta\pm\sqrt{\Delta^2+|g|^2}\over 2}$$

so the differential equation itself has the solution:

$$c_a(t)=e^{-i\Delta t/2}\left(\alpha e^{i\sqrt{{\Delta}^2+|g|^2}t/2}+\beta e^{-i\sqrt{{\Delta}^2+|g|^2}t/2}\right)\,.$$

This, we need to emphasize again, is exact.

It is useful at this point to introduce the Rabi frequency:

$$\Omega_\mathrm{R}\equiv{1\over2}\sqrt{|g^2|+\Delta^2}$$

in terms of which the probability amplitude for the ground state reads:

$$c_a(t)=e^{-i\Delta t/2}\left(\alpha e^{i\Omega_\mathrm{R}t}+\beta e^{-i\Omega_\mathrm{R}t}\right)\,.$$

Now to obtain $c_b$ we can substitute the solution we found for $c_a$ back into the original differential equations, specifically in $\dot c_a={g\over2}e^{-i\Delta t}c_b$. This gives us:

$$c_b(t)={ie^{i\Delta t/2}\over g}\left(\alpha e^{i\Omega_\mathrm{R}t}\left[2\Omega_\mathrm{R}-\Delta\right]-\beta e^{-i\Omega_\mathrm{R}t}\left[2\Omega_\mathrm{R}+\Delta\right]\right)$$

which is more complicated as it needs to accommodate for the initial condition set by $c_a$. To describe the general situation where one starts in the ground state with probability amplitude $A$ and in the excited state with probability amplitude $B$, we need to find $\alpha$ and $\beta$ such that, for any detuning $\Delta$, we have:

\begin{align} \alpha+\beta&=A\\ {i\over g}(\alpha(2\Omega_\mathrm{R}-\Delta)-\beta(2\Omega_\mathrm{R}+\Delta))&=B \end{align}

which is solved for $\alpha$ and $\beta$ as:

\begin{align} \alpha&={A(2\Omega_\mathrm{R}+\Delta)-Big\over \Omega_\mathrm{R}}\\ \beta&={A(2\Omega_\mathrm{R}-\Delta)+Big\over \Omega_\mathrm{R}} \end{align}

where $Big$ is, of course, $i$ (Euler number) times $Bg$ (probability amplitude times coupling strenght). In these formulae, normalization demands that $|A|^2+|B|^2=1$. Particular cases of interest include resonance, in which case

$$ \begin{align} \alpha&={1\over 2}\left(A-iB\right)\\ \beta&={1\over2}(A+iB) \end{align} $$

i.e., $\alpha=z/2$ and $\beta=z^*/2$ for some complex number $z$ on the unit circle (i.e., such that $|z|^2=1$). In this case, one has full-amplitude Rabi oscillations of the type:

\begin{align} c_a(t)&={e^{-i\Delta t\over2}}\operatorname{Re}(ze^{i\Omega_\mathrm{R}t})/2\,,\\ c_b(t)&={-e^{i\Delta t\over2}}\operatorname{Im}(ze^{i\Omega_\mathrm{R}t})/2\,, \end{align}

i.e., full amplitudes trajectories on a circle, whose phase dynamics is set by the initial condition. This is not a coincidence as Rabi oscillations turn out to be great-circles on a sphere (the so-called Bloch sphere) as we shall see next Semester when we study the dynamics of a so-called qubit and learn new ways to look at quantum states (wavefunctions) of such systems. Here we will we content ourselves with a few examples of typical Rabi dynamics:

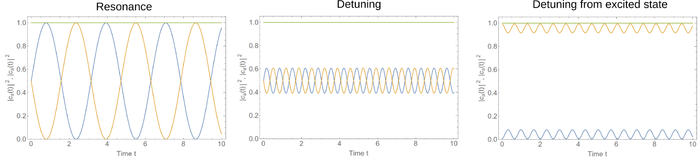
At resonance, all the populations are swept over, so the phase decides which is the initial condition. With detuning, this becomes an independent parameter. A Mathematica notebook is provided for you to explore dynamically: RabiOscillations.nb.