The 2D Harmonic Oscillator

(Part of the Wolverhampton Lectures of Physics's Quantum Physics Course)

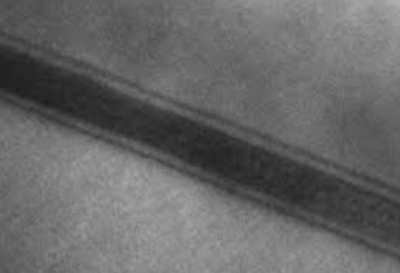
Today we will restrict ourselves to an intermediate situation of a 2D space, because that is the simplest way to extend the 1D case and this makes the 3D case clear enough (so we leave it as an exercise to you). In fact, particles can be restricted to 2D, for instance in the solid-state, so this happens to be a very important case as well! The picture below shows a cross-section micrograph through TEM (Transmission Electronic Microscopy) of a so-called quantum well, namely, a GaInAs quantum well (of 7.5 nm width). Electrons would be confined inside this dark area and thus unable to move in what is roughly the z dimension here. The would however wander freely within the plane (perpendicular to the screen). This will be described with a 2D Schrödinger equation.

We will also start to introduce nontrivial potentials, starting with the quadratic potential. This describes either a particle in this potential, or the harmonic oscillator (so that we also describe the 2D harmonic oscillator). Schrödinger equation reads, in this case (we call $\mu$ the mass of the particle as $m$ will be used as an index later):

$$\displaystyle-{\hbar^2\over2\mu}\nabla^2\psi(x,y)+V(x,y)\psi(x,y)=E\psi(x,y)$$

where $$V(x,y)={\mu\omega^2\over2}(x^2+y^2)$$

and $$\nabla^2=\partial_x^2+\partial_y^2\,.$$

Thanks to this particular form of the potential, we can actually collect all the $x$ terms together and all the $y$ terms together, which invites the separation of variables:

$$ \psi(x,y)=X(x)Y(y) $$

as indeed Schrödinger equation can then be written as (after dividing both sides by $XY$):

$$\displaystyle\left(-{1\over X}{\hbar^2\over 2\mu}{\partial^2X\over\partial x^2}+{1\over2}\mu\omega^2 x^2\right) + \left(-{1\over Y}{\hbar^2\over 2\mu}{\partial^2Y\over\partial y^2}+{1\over2}\mu\omega^2 y^2\right)=E$$

which are actually two uncoupled 1D Schrödinger equations, also for the harmonic trap! (just in 1D, this time). We know the solution for these from last year, in terms of the Hermite polynomials $H_n$:

$$\begin{align} X_n(x)&={1\over\pi^{1/4}\sqrt{2^{n}n!}}H_n(x)\exp(-x^2/2)\\ Y_m(y)&={1\over\pi^{1/4}\sqrt{2^{m}m!}}H_m(x)\exp(-y^2/2) \end{align}$$

after rescaling $(x,y)\rightarrow(\sqrt{\mu\omega/\hbar})(x,y)$ and with $n, m$ integers that label the states, with respective energies $E_n=(n+1/2)\hbar\omega$. Therefore, the 2D harmonic oscillator has solutions:

$$\displaystyle\psi_{n,m}(x,y)={1\over\sqrt{\pi 2^{n+m}n!m!}}H_n(x)H_m(y)\exp(-(x^2+y^2)/2)$$

with associated energy

$$ E_{n,m}=(n+m+1)\hbar\omega $$

The spectrum is easily found in this case (it is much simpler than the square box):

with degeneracy $(n+1)$ for the $n$th state.