Two particles in 1D
We carry on our program of considering several quantum objects at once. We have studied a lot the single particle, for instance in various potential wells (square well, delta well, etc.) This was mainly in 1D, in which case the wavefunction was $\psi(x,t)$ with the modulus square giving the density of probability to find the particle at position $x$ at time $t$. We also considered a particle in 2D or 3D. For the 2D case, for instance, we upgraded the wavefunction to $\psi(x,y,t)$ with the modulus square giving the density of probability to find the particle at position $(x,y)$ at time $t$. We now return to the 1D case (for simplicity), but with two particles. Maybe surprisingly, this will turn out to be very connected to the 2D case of a single particle:
We can still apply the same trick of separation of variables for the space and time coordinates, so we will get rid of time in the following. Solving for the eigenstates will yield the most general solution by linear superpositions.
Therefore, we now consider the eigenstates of two 1D particles. Instead of $(x,y)$, we will write $(x_1,x_2)$ to highlight that the variables correspond to the $x$-positions (on the same axis) of two particles. In this case, their joint wavefunction reads:
$$\psi(x_1,x_2)$$
and their respective operators act on the corresponding slices of the Hilbert tensor product, e.g., the kinetic energy is $-\hbar^2\partial_{x_1}/(2m_1)$ for particle 1 (assuming it has a mass $m_1$) and $-\hbar^2\partial_{x_2}/(2m_2)$ for particle 2 (with mass $m_2$). The same holds for the position operators, which are $x_1$ and $x_2$, respectively.
The potential can also have some effect on one particle only (if they aren say, of different type, e.g., one is charged and feels an electrostatic potential while the other is not and does not feel it). In this case, such a potential applies only to the corresponding slice of the tensor product, and carries along the identity for the other part that concerns the other particle. If both particles feel the same potential, then it is symmetric. As a result, assuming such a case and also that both particles have the same mass, $m_1=m_2$, then we find, interestingly, that the two 1D particle Schrödinger equation
$$-i\hbar\partial_t\psi(x_1,x_2,t)=\left[-{\hbar^2\over2m}(\partial_{x_1}+\partial_{x_2})+V\right]\psi(x_1,x_2,t)$$
is exactly the same, as far as the mathematical structure is concerned, than for one 2D particle, since indeed $\partial_{x_1}+\partial_{x_2}=\nabla^2$ (we would write $x$ and $y$ rather than $x_1$ and $x_2$ for a 2D particle, but this is just an irrelevant notation: the equation is the same).
This is welcome since we have already solved many one 2D-particle problems... so it seems that much of the work has been done already. And this is indeed the case, but there is one axiom or postulate more that we need to take into consideration. The function does not factorize in general, i.e., $\psi(x_1,x_2)$ is different from $\phi(x_1)\varphi(x_2)$ for two functions $\phi$ and $\varphi$ of one-variable (for the corresponding particle). The joint product $\psi(x_1,x_2)$ that connects the two particles through their variables is what describes a general state of two quantum objects together, as per the tensor products rules. When it is the case that $\psi(x_1,x_2)\neq \phi(x_1)\varphi(x_2)$, then the particles have correlations or are correlated. This can be induced by interactions, typically. But there is a more fundamental source of "correlations" in quantum mechanics.
A fundamental postulate of quantum mechanics is that two particles of the same species (e.g., two electrons, two photons, etc.) are indistinguishable. What does it mean? Let us assume that the two states $\phi$ and $\varphi$ that described the individual particles are orthogonal (as well as, of course, normalized). For instance, this could be the ground state and first excited state of the infinite square well. Assuming that two indistinguishable electrons are in these two states, means that one electron is in the ground state, the other in the excited state but that we cannot say "which is which", i.e., we cannot refer to the "1st electron" or "this electron" or "electron A". Indistinguishable means "one electron, but we don't know which and have no way to". So the total state cannot be :
$$\psi(x_1,x_2)=\phi(x_1)\varphi(x_2)$$
because that identifies the electrons! Namely, by their position: the electron at $x_1$ (is the one in the ground state) and the electron at $x_2$ (is the excited one). Quantum mechanics postulates, however, that we cannot refer to the $x_1$ and $x_2$ electrons (which are indeed just other names for them). To make them indistinguishable, we must make the case above or indistinguishable from the other-way-around configuration where the electron at $x_1$ is the one in the excited state and that at $x_2$ in the ground state:
$$\phi(x_2)\varphi(x_1)\,.$$
As is commonplace in quantum mechanics, as indeed was the case for the $|10\rangle={1\over\sqrt2}(|\uparrow\downarrow\rangle+|\downarrow\uparrow\rangle)$ state of two spin 1/2 canceling their $z$-projection, when two things can occur, they occur simultaneously, by way of a linear superposition of the possibilities:
$$\psi(x_1,x_2)={1\over\sqrt{2}}\left(\phi(x_1)\varphi(x_2)+\phi(x_2)\varphi(x_1)\right)\,.$$
This indeed describes the situation where we do not assign an individuality to the underlying particles since they are both in the two states, so neither is in one particular state. One can check that swapping the two particles, $x_1\leftrightarrow x_2$, indeed leaves the wavefunction untouched. In fact, one really needs that the observables remain untouched, not the wavefunction itself, but its modulus square. In fact, and again as was the case for spin that also came with the possibility of an out-of-phase superposition of the possibilities, i.e., $|00\rangle={1\over\sqrt2}(|\uparrow\downarrow\rangle-|\downarrow\uparrow\rangle)$, one can similarly antisymmetrize the total wavefunction with the effect that swapping the particles changes the total sign (with no observable consequences):
$$\psi(x_1,x_2)={1\over\sqrt{2}}\left(\phi(x_1)\varphi(x_2)-\phi(x_2)\varphi(x_1)\right)\,.$$
It may actually also be the case of a complex-valued superposition in some particular cases to make particles indistinguishable in lower dimensions, but this is all very exotic physics. The $\pm$ cases are important, because they separate two types of particles:
- $+$ are so-called bosons.
- $-$ are so-called fermions.
It so happens (this can be demonstrated when including special relativity to the theory but is an axiom in our current non-relativistic exposition) that:
- Full-spin particles are bosons (so with symmetric wavefunctions)
- Half-integer spin particles are fermions (with antisymmetric wavefunctions).
This has observable consequences, prominently, the averages of operators on symmetric, antisymmetric or with nothing done to them (for particles that are distinguishable, like an electron and a proton) are different, with a tendency to bring bosons together and repel fermions as compared to distinguishable particles, which provide an uncorrelated reference. We can compute all the cases at once introducing:
$$|\psi\rangle_\varsigma=A_\varsigma\left(|\psi_a\rangle|\psi_b\rangle+\varsigma|\psi_b\rangle|\psi_a\rangle\right)$$
where $A_\varsigma=\begin{cases} -1 & \text{for fermions}\\ 0 & \text{for classical particles}\\ 1 & \text{for bosons} \end{cases}$
with normalization constant
$$A_\varsigma=\sqrt{\frac{2-|\varsigma|}{2}}\,,$$
which is a compact notation to say that it is $1/\sqrt2$ for indistinguishable particles (bosons and fermions) and $1$ for classical particles.
The quantum average for a generic operator $\Omega$ then reads:
$$\langle\Omega\rangle=A_\varsigma^2\left(\langle\psi_b|\langle\psi_a|+\varsigma\langle\psi_a|\langle\psi_b|\right)\Omega\left(|\psi_a\rangle|\psi_b\rangle+\varsigma|\psi_b\rangle|\psi_a\rangle\right)$$
which one can distribute according to the linear-algebraic feel of tensor products:
$$\begin{align} \langle\Omega\rangle= A_\varsigma^2 \big(&\langle\psi_b|\langle\psi_a|\Omega|\psi_a\rangle|\psi_b\rangle\\ +\varsigma&\langle\psi_b|\langle\psi_a|\Omega|\psi_b\rangle|\psi_a\rangle\\ +\varsigma&\langle\psi_a|\langle\psi_b|\Omega|\psi_a\rangle|\psi_b\rangle\\ +\varsigma^2&\langle\psi_a|\langle\psi_b|\Omega|\psi_b\rangle|\psi_a\rangle \big) \end{align}\,.$$
Now assuming a general type of operator $\Omega=\Omega_1\otimes\Omega_2$, the previous expression evaluates to:
$$\begin{align} \langle\Omega\rangle= A_\varsigma^2 \big(&\langle\psi_a|\Omega_1|\psi_a\rangle\langle\psi_b|\Omega_2|\psi_b\rangle\\ +\varsigma&\langle\psi_a|\Omega_1|\psi_b\rangle\langle\psi_b|\Omega_2|\psi_a\rangle\\ +\varsigma&\langle\psi_b|\Omega_1|\psi_a\rangle\langle\psi_a|\Omega_2|\psi_b\rangle\\ +\varsigma^2&\langle\psi_b|\Omega_1|\psi_b\rangle\langle\psi_a|\Omega_2|\psi_a\rangle \big) \end{align}\,.$$
If, for convenience of notation, we write:
$$\begin{align} &\langle\Omega_i\rangle_c\equiv\langle\psi_c|\Omega_i|\psi_c\rangle\quad\text{for $i=1,2$ and $c=a,b$}\\ &\langle\Omega_i\rangle_{ab}\equiv\langle\psi_a|\Omega_i|\psi_b\rangle\quad\text{for $i=1,2$} \end{align}$$
then the above average reads:
$$\langle\Omega_1\Omega_2\rangle=A_\varsigma^2 \big\{ \langle\Omega_1\rangle_a \langle\Omega_2\rangle_b % &+\varsigma\langle\Omega_1\rangle_{ab}^*\langle\Omega_2\rangle_{ab}\\ +\varsigma^2\langle\Omega_1\rangle_b \langle\Omega_2\rangle_a +2\varsigma\Re\left(\langle\Omega_1\rangle_{ab} \langle\Omega_2\rangle_{ab}^*\right) \big\}\,.$$
If $\Omega_1$ and~$\Omega_2$ are the same operators on their respective Hilbert spaces, so that for all $c$ for some basis of states $|\psi_c\rangle$ we have $\langle\Omega_1\rangle_c=\langle\Omega_2\rangle_c$, then we find:
$$\langle\Omega_1\Omega_2\rangle= \langle\Omega_1\rangle_a \langle\Omega_2\rangle_b % &+\varsigma\langle\Omega_1\rangle_{ab}^*\langle\Omega_2\rangle_{ab}\\ +\varsigma|\langle\Omega_1\rangle_{ab}|^2$$
since $A_\varsigma^2(1+\varsigma^2)=\frac{2-\varsigma^2}{2}(1+\varsigma^2)=1$ and $2A_\varsigma^2\varsigma=\varsigma$ (note that $\varsigma^4=\varsigma^2$).
The term $|\langle\Omega_1\rangle_{ab}|^2$ (which is equal to $|\langle\Omega_2\rangle_{ab}|^2$ per assumption of this configuration) cancels for classical (distinguishable) particles but brings positive or negative correlations due to the symmetry of the wavefunction for quantum (indistinguishable) particles.
Let us consider for instance the positions, i.e., $\Omega_i=x_i$ for $i=1, 2$ and compute the average square distance between the particles. Since
$$\langle(x_1-x_2)^2\rangle=\langle x_1^2\rangle+\langle x_2^2\rangle-2\langle x_1x_2\rangle$$
the general result above gives us the correlation term as:
$$\langle x_1x_2\rangle=\langle x\rangle_a\langle x\rangle_b+\varsigma|\langle x\rangle_{ab}|^2$$
which inserted back in the quantity we compute gives:
$$\langle(x_1-x_2)^2\rangle=\langle x^2\rangle_a+\langle x^2\rangle_b-2\langle x\rangle_a\langle x\rangle_b-2\varsigma|\langle x\rangle_{ab}|^2\,.$$
The first three terms correspond to the classical result:
$$\langle(\Delta x)\rangle^2_\mathrm{C}=\langle x^2\rangle_a+\langle x^2\rangle_b-2\langle x\rangle_a\langle x\rangle_b$$
so that we have, in general:
$$\langle(\Delta x)\rangle^2_\varsigma=\langle(\Delta x)\rangle^2_\mathrm{C}-2\varsigma|\langle x\rangle_{ab}|^2$$
that is, explicitly for bosons and fermions:
$$\langle(\Delta x)\rangle^2_\pm=\langle(\Delta x)\rangle^2_\mathrm{C}\mp 2|\langle x\rangle_{ab}|^2$$
We see that bosons ($+1$) tend to be found closer together as compared to classical particles, while fermions ($-1$) on the contrary tend to be found farther apart. The departure comes from the term $\langle x\rangle_{ab}$ that mixes the two states through the operators. This is known as as overlap integral. For the case of position:
$$\langle x\rangle_{ab}\equiv\int x\psi_a(x)^*\psi_b(x)\,dx\,.$$
The term is significant only if $\psi_a$ and $\psi_b$ indeed overlap appreciably. Two electrons that do not "see" each other are indeed indistinguishable.
Although this is a purely geometric contribution, it seems to behave as a sort of force, drawing together or pulling apart the particles. It is known as the exchange force (although it is not, again, a force). It has momentous implications, as we shall see later on and repeatedly, on many aspects of the physics of light and matter.
Let us keep making this general phenomenon more concrete by turning now to particular states in a given problem. Consider, for instance, two non-interacting and particles, of mass $m$, in the infinite square well. We remind the wavefunctions:
$$\psi(x) = \sqrt{\dfrac{2}{L}}\sin{\dfrac{n\pi}{L}}x\,.$$
Let us assume, then, that one particle is in the ground state and the other in the first excited state. Their combined wavefunctions, would the particles be indistinguishable, would be:
$$\Psi_0(x_1,x_2)=2\sin(\pi x_1)\sin(2\pi x_2)\,.$$
The symmetrized/antisymmetrized wavefunctions, on the other hand, read:
$$\Psi_\pm(x_1,x_2,t)={\sqrt{2}}\{\sin(\pi x_1)\sin(2\pi x_2)\pm\sin(\pi x_2)\sin(2\pi x_1)\}\,.$$
This is how the joint density probability looks like for the three types of non-interacting particles:
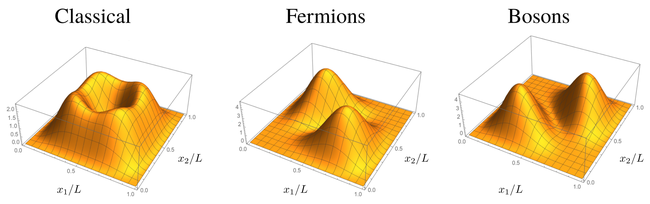
where we have brought, for fairness or accuracy of comparison, a classical indeterminacy $P(x_1,x_2)={1\over2}\{|\psi_0(x_1,x_2)|^2+|\psi_0(x_2,x_1)|^2\}$ for the choice of which particle is excited and which is not in the classical case:
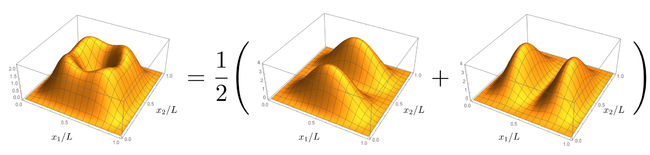
Here it is important to remember the early Heisenberg and Schrödinger's warnings against understanding the wavefunction as a wave of some physical object in space. Instead, we have a mathematical description in some abstract parameter or configuration space. What we see is that in the bosonic case the particles clutter on the diagonal while they avoid the diagonal in the fermionic cases. In both cases, they avoid being both at the center since the first excited state vetos this position. We can try to get more intuition about this phenomenon by looking at 1D quantities, since it is always more tricky to think (correctly) in 2D. First, it is important to understand that this is intrinsically a two-particle effect. If we "trace-over" (a term that we use in quantum mechanics to mean "average over", we will see the reason why later) one particle, we find for the reduced probability distribution of the other one:
$$|\psi_1(x)|^2\equiv\int_0^L|\Psi_\varsigma(x_1,x_2)|^2\,dx_1=\sin(\pi x)^2+\sin(2\pi x)^2\tag{1}$$
which is, clearly, independent of $\varsigma$. One particle in isolation is found with the same probability regardless of its statistical behaviour to the other. This is in stark contrast with two-particle observables, e.g., the probability (density) to find both particles at the same position on the diagonal or symmetrically positioned around the center of the box on the antidiagonal:
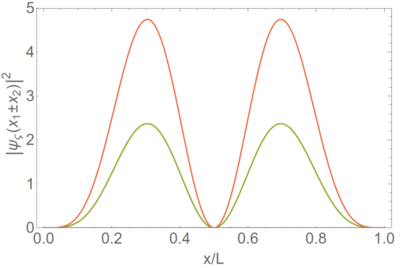
The classical result is shown in green. The red line shows bosons on the diagonal (fermions are zero in this case) and fermions on the antidiagonal (bosons are zero in this case). One is twice the other, so it twice more likely to find both particles sitting on top of each other when they are bosons than when they are classical while it becomes impossible if they are fermions. This has observable consequences, although not at the single particle level, i.e., when plotting some observable that results from averaging over one-particle quantities. For instance, the animation below shows the distribution of positions after a statistical average of the positions for many two-particle detections. The three curves are identical (click the image to zoom/restart the animation):
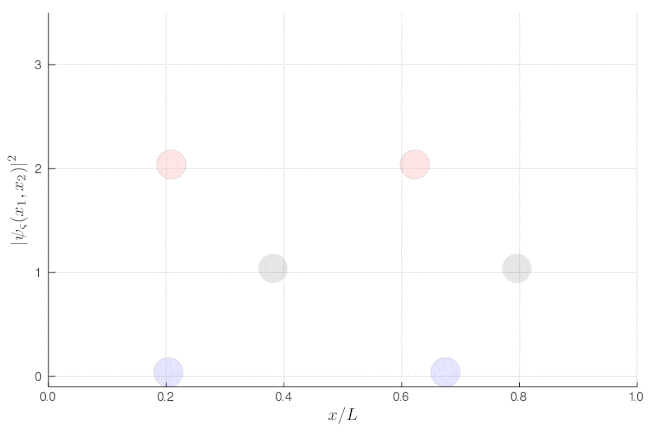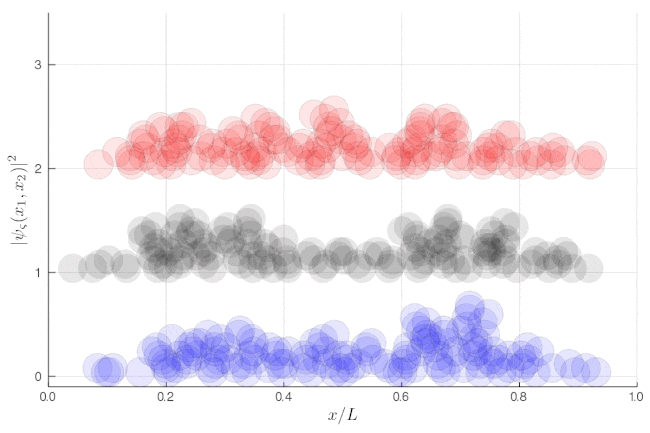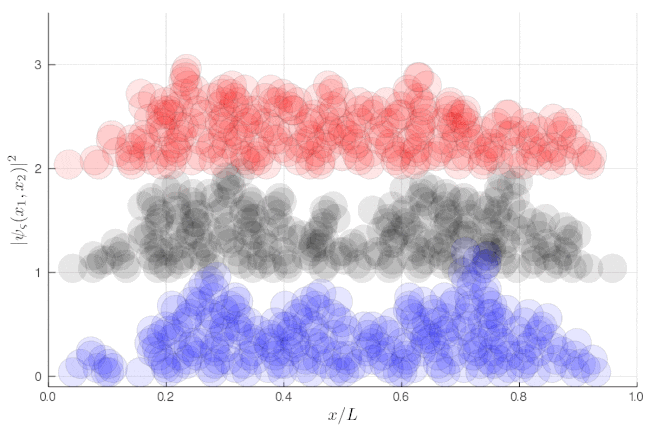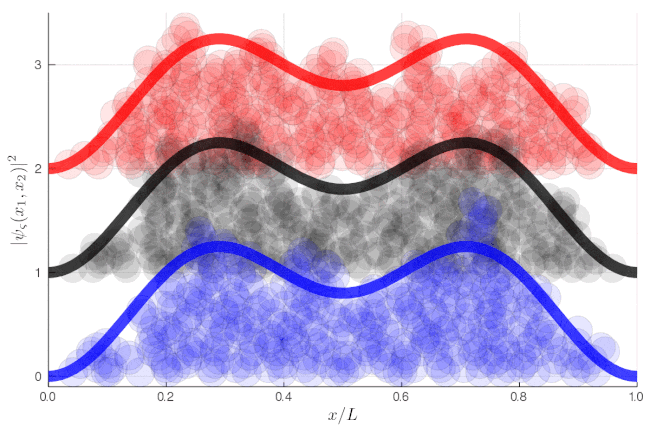
The traces at the end of the animations show Eq. (1), i.e., the same result regardless of the type of particles.
If instead of such averages over single-particle properties, we now focus on two-particle properties, one can see very strong correlations. This shows the same as above, but without the binning:
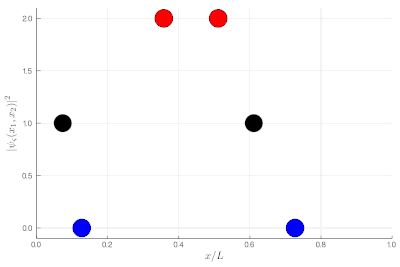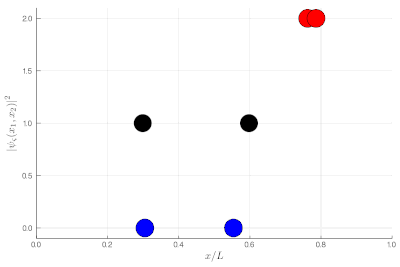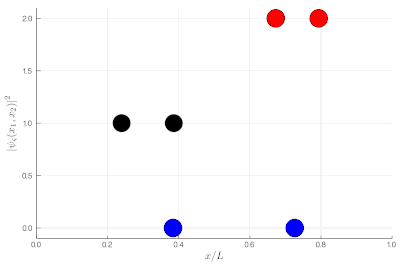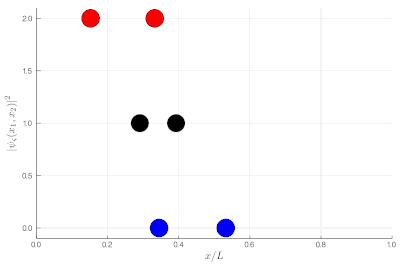
Here, one sees that the red particles display tend to clutter together, as if attracted to each other, a property known as "bunching". The blue display the opposite "antibunching" of avoiding each-other, as if repelled the one by the other. The black don't care and are just randomly distributed according to their state in the box. If it's not clear, you can look at half of the box: while you see 0, 1 or 2 black particles with the same probability, you see 2 red together (or absent, both on the other side) and 1 blue particle alone, with probability ~86% (we let you compute the exact value as an exercise):
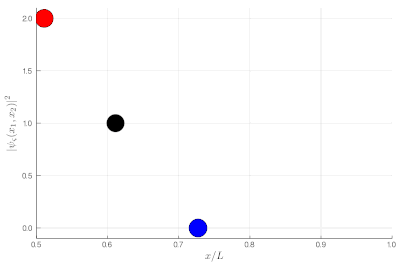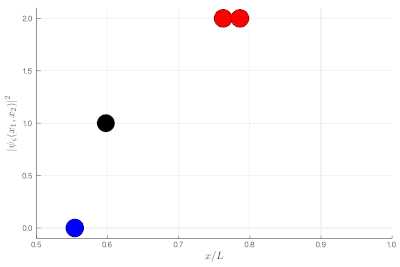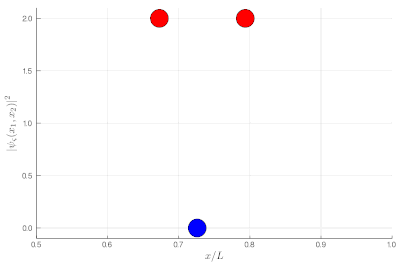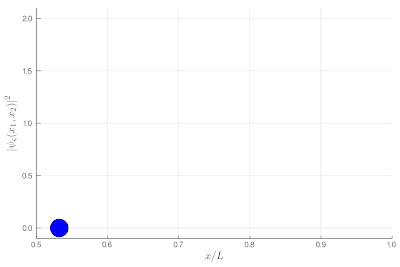
If this is still not clear enough, once you measure two-particle observables, you can plot these instead. This is a histogram of relative distances, with a celebrated property of indistinguishable particles: red are twice as likely as black to sit on top of each other while blue can never do so:
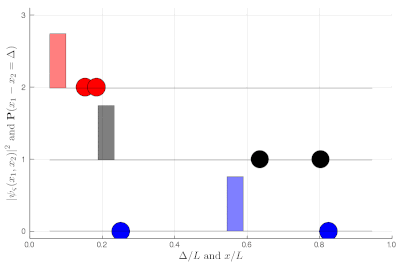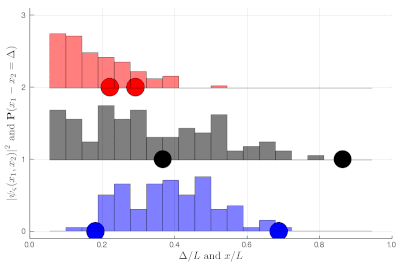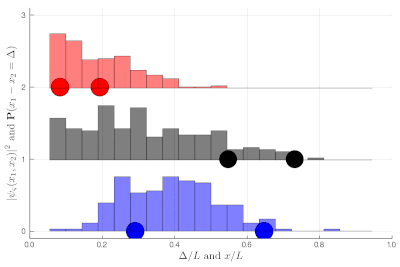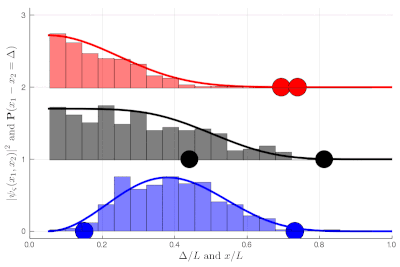
Here again, we let you compute the exact (theoretical) distribution, which is displayed towards the end of the animation, as an exercise. It is now clear that the red particles are much closer to each other on average than the black ones, which are more uniformly distributed in the box until they start to feel the border of the box. The blue, in an even more marked fashion, clearly avoid proximity, with the distribution vanishing at the origin! All this happens without interactions, this is a consequence of particles' indistinguishability knitted at the wavefunction level.
Correlation is a big topic of quantum mechanics! In the general case, of course, we have several particles moving in high-dimensional spaces. Effects become even stronger in these cases, and drive famous phases of matter such as Bose-Einstein condensate, where a huge amoung of bosons collapse onto a macroscopic wavefunction. This is at the heart of the physics of superconductors and superfluids. The "super" refers to the emergence of quantum effects into our classical world.