m |
m (→Hydrogen wavefunctions) |
||
| Line 1: | Line 1: | ||
= Hydrogen wavefunctions = | = Hydrogen wavefunctions = | ||
| − | |||
| − | |||
Now that we have the closed-form analytical expressions for the Hydrogen wavefunctions, namely: | Now that we have the closed-form analytical expressions for the Hydrogen wavefunctions, namely: | ||
| Line 7: | Line 5: | ||
$${\displaystyle \psi _{n\ell m}(r,\theta ,\varphi )={\sqrt {{\left({\frac {2}{na_{0}^{*}}}\right)}^{3}{\frac {(n-\ell -1)!}{2n(n+\ell )!}}}}e^{-\rho /2}\rho ^{\ell }L_{n-\ell -1}^{2\ell +1}(\rho )Y_{\ell }^{m}(\theta ,\varphi )}$$ | $${\displaystyle \psi _{n\ell m}(r,\theta ,\varphi )={\sqrt {{\left({\frac {2}{na_{0}^{*}}}\right)}^{3}{\frac {(n-\ell -1)!}{2n(n+\ell )!}}}}e^{-\rho /2}\rho ^{\ell }L_{n-\ell -1}^{2\ell +1}(\rho )Y_{\ell }^{m}(\theta ,\varphi )}$$ | ||
| − | (where $\rho=2r/(na_\mathrm{B})$, $L$ are Laguerre polynomials $Y$ spherical harmonics) we can turn to the problem of their visualisation. | + | (where $\rho=2r/(na_\mathrm{B})$, $L$ are Laguerre polynomials $Y$ spherical harmonics) we can turn to the problem of their visualisation. This will allow us to get one insight into the problem of comprehending how physical reality relates to its mathematical description. The wavefunctions of hydrogen in real-space represent probability amplitudes for the electron to be located at a particular position. They remind of actual waves that are pinned (standing waves) to the nucleus, so the temptation is great to think of them as orbiting electron clouds. They go by the names, incidentally, of orbitals. This is a largely incorrect picture, as was appreciated from the early days of quantum mechanics. To this day, nobody knows what exactly is an electron and how it does bind to its nucleus. As a zero-th order approximation of visualizing the electron, we will content to consider the much simpler problem of visualising its mathematical wavefunction. This is a 3D complex-valued field, so in principle it is not such a big deal. This can be pretty much achieved through 2D density plots. That, however, restrains severely the geometrical structure, in terms of lobes and rings, which is better seen in 3D. |
| − | + | They extend to much extent to all atoms, as we shall see in the coming lectures, where they are called "atomic orbitals". | |
| − | + | We first remind the mathematical classification of the states. For hydrogen, the stationary orbitals are specified by three quantum numbers: | |
$$n,\quad l\quad\text{and}\quad m$$ | $$n,\quad l\quad\text{and}\quad m$$ | ||
| Line 20: | Line 18: | ||
* The number $m$, or magnetic quantum number, can take negative values, and is bounded in absolute value by $l$: $-l\le m\le l$. It describes, qualitatively, the orientation of the orbital. | * The number $m$, or magnetic quantum number, can take negative values, and is bounded in absolute value by $l$: $-l\le m\le l$. It describes, qualitatively, the orientation of the orbital. | ||
| − | |||
The $s$ subshells are shaped like spheres, with the ground state being simply a fading ball. Higher $n$ with $l=0$ have radial (spherical) symmetry but with oscillations due to destructive interferences. The $s$ orbitals are the only ones with an antinode at the centre (where the nucleus is) while other orbitals present a node there. This does not invalidate the model, though, as the probability for the electron to be actually found there remain negligible. | The $s$ subshells are shaped like spheres, with the ground state being simply a fading ball. Higher $n$ with $l=0$ have radial (spherical) symmetry but with oscillations due to destructive interferences. The $s$ orbitals are the only ones with an antinode at the centre (where the nucleus is) while other orbitals present a node there. This does not invalidate the model, though, as the probability for the electron to be actually found there remain negligible. | ||
| Line 62: | Line 59: | ||
, {x, -30, 30}, {y, -30, 30}, {z, -30, 30}, ColorFunction -> Hue, ColorFunctionScaling -> True, Boxed -> False, Axes -> False, PlotLabel -> Style[StringForm["Hydrogen atom orbitals\n |\[Psi]\!\(\*SuperscriptBox[\(|\), \\(2\)]\) : n=`` l=`` m=``", n, l, m], Medium, FontFamily -> "DejaVu Serif"], LabelStyle -> {Black, Bold}, RegionFunction -> Function[{x, y, z}, x < 0 || y > 0], PlotLegends -> Automatic], {n, 1, 4}, {l, 0, n - 1}, {m, -l, l}] | , {x, -30, 30}, {y, -30, 30}, {z, -30, 30}, ColorFunction -> Hue, ColorFunctionScaling -> True, Boxed -> False, Axes -> False, PlotLabel -> Style[StringForm["Hydrogen atom orbitals\n |\[Psi]\!\(\*SuperscriptBox[\(|\), \\(2\)]\) : n=`` l=`` m=``", n, l, m], Medium, FontFamily -> "DejaVu Serif"], LabelStyle -> {Black, Bold}, RegionFunction -> Function[{x, y, z}, x < 0 || y > 0], PlotLegends -> Automatic], {n, 1, 4}, {l, 0, n - 1}, {m, -l, l}] | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| + | |||
| + | orbitals of multi-electron atoms are qualitatively similar to those of hydrogen | ||
= Links = | = Links = | ||
Revision as of 14:01, 3 March 2021
Hydrogen wavefunctions
Now that we have the closed-form analytical expressions for the Hydrogen wavefunctions, namely:
$${\displaystyle \psi _{n\ell m}(r,\theta ,\varphi )={\sqrt {{\left({\frac {2}{na_{0}^{*}}}\right)}^{3}{\frac {(n-\ell -1)!}{2n(n+\ell )!}}}}e^{-\rho /2}\rho ^{\ell }L_{n-\ell -1}^{2\ell +1}(\rho )Y_{\ell }^{m}(\theta ,\varphi )}$$
(where $\rho=2r/(na_\mathrm{B})$, $L$ are Laguerre polynomials $Y$ spherical harmonics) we can turn to the problem of their visualisation. This will allow us to get one insight into the problem of comprehending how physical reality relates to its mathematical description. The wavefunctions of hydrogen in real-space represent probability amplitudes for the electron to be located at a particular position. They remind of actual waves that are pinned (standing waves) to the nucleus, so the temptation is great to think of them as orbiting electron clouds. They go by the names, incidentally, of orbitals. This is a largely incorrect picture, as was appreciated from the early days of quantum mechanics. To this day, nobody knows what exactly is an electron and how it does bind to its nucleus. As a zero-th order approximation of visualizing the electron, we will content to consider the much simpler problem of visualising its mathematical wavefunction. This is a 3D complex-valued field, so in principle it is not such a big deal. This can be pretty much achieved through 2D density plots. That, however, restrains severely the geometrical structure, in terms of lobes and rings, which is better seen in 3D.
They extend to much extent to all atoms, as we shall see in the coming lectures, where they are called "atomic orbitals".
We first remind the mathematical classification of the states. For hydrogen, the stationary orbitals are specified by three quantum numbers:
$$n,\quad l\quad\text{and}\quad m$$
- The number $n$ or principal quantum number can take any positive integer value, $n=1, 2, \cdots$. It describes the energy and also the average distance of the electron from the nucleus, thus, qualitatively, its size. Orbitals with the same $n$ are, for this reason, collectively described as belonging to the same "shell". It already appears in the Bohr model.
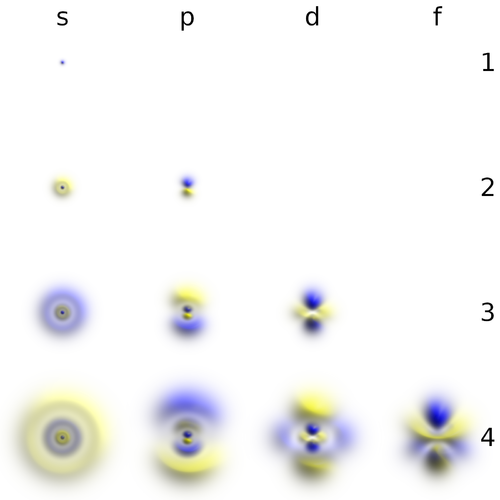
- The number $l$, or azimuthal quantum number, describes the rotation, or angular momentum, of the electron. It describes, qualitatively, the shape of the orbital. It is an integer, possibly and always at least zero, otherwise strictly bounded by the principal quantum number: $0\le l\le n-1$. The orbitals with the same $n$ and $l$ are called "subshells". They are denoted $s$ (sharp) for $l=0$, $p$ (principal) for $l=1$, $d$ (diffuse) for $l=2$ and $f$ (fundamental) for $l=3$ due to historical reasons (?!) and proceed beyond that alphabetically at the exception of j which is skipped: $g, h, i, k, l, \cdots$ This gives rise to naming such as 1s ($n=1, l=0$, i.e., the ground state) or $2p$ ($n=2$, $l=1$).
- The number $m$, or magnetic quantum number, can take negative values, and is bounded in absolute value by $l$: $-l\le m\le l$. It describes, qualitatively, the orientation of the orbital.
The $s$ subshells are shaped like spheres, with the ground state being simply a fading ball. Higher $n$ with $l=0$ have radial (spherical) symmetry but with oscillations due to destructive interferences. The $s$ orbitals are the only ones with an antinode at the centre (where the nucleus is) while other orbitals present a node there. This does not invalidate the model, though, as the probability for the electron to be actually found there remain negligible.
There are three $p$-orbitals (starting at $n=2$) corresponding to $m=\pm1$ and 0. They each have the form of two ellipsoids pointing in opposite directions and pinned by a node at the nucleus, and are otherwise perpendicularly oriented the ones from the others, which one can align with the Cartesian axis vectors $\hat\imath$, $\hat\jmath$ and $\hat k$.
There are five $d$-orbitals (starting at $n=3$) corresponding to $m=\pm2, \pm1$ and 0.
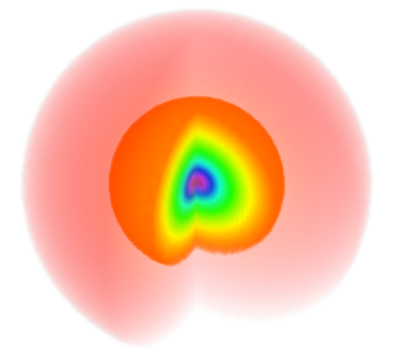
The color code is such that yellowish-orangeish-redish colors fade into zero and blueish-purplish or (confusingly, extremely red) colors peak into the highest values (see it here exactly for $\psi_{100}$)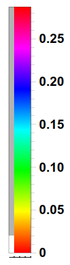
In contrast to the real-valued orbitals in chemistry, which are superpositions of several m-eigenstates, the probability densities shown here are symmetric around the z-axis.
When $l\neq 0$, the problem becomes non-radially symmetric and raises one step up in complexity. Given the structure of the solution $\psi_{nlm}=R_nY_l\m$, it basically reduces to the visualization of the spherical harmonics, that are represented here in 3D with the radial distance giving the magnitude of the function for each $(\theta, \phi)$ angles (which is possible to do since spherical harmonics are defined on the sphere and do not depend on $r$):
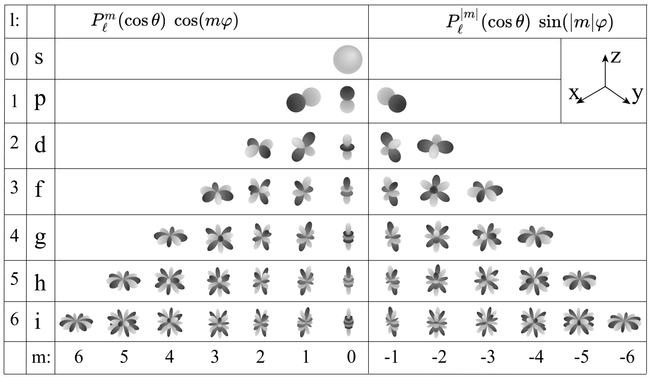
Of course when plotting in 3D it is possible to make it more or less pretty (see here for a 3D rendered version).
This representation [1]—from Geek3—shows solid bodies that enclose a volume of space where the probability density exceeds a threshold that has been chosen to produce nice-looking results. The color depicts the phase of the complex-valued wavefunction at the corresponding point. The 2s, 3s and 4s orbitals are cut open to reveal the inner structure. The wavefunctions are in the basis or orbitals that are symmetric around the $z$ axis. This representation finds over variations here.
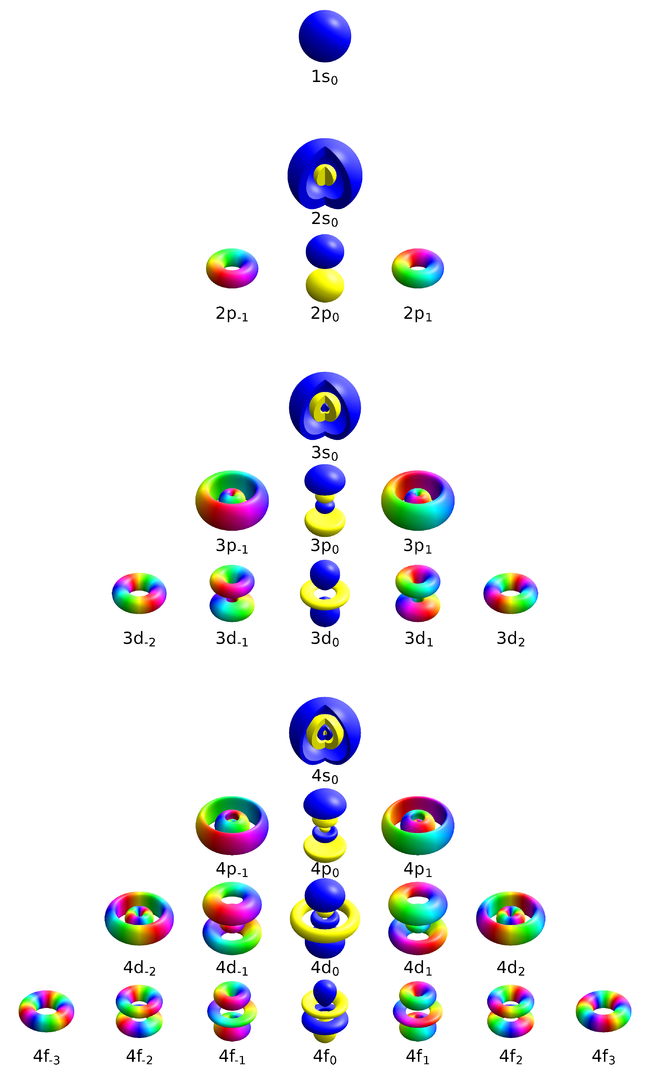
This representation [2], also by Geek3, uses transparency and 3D rendering of the with the colour depicting the sign of $\psi$. The cloud gives a more realistic representation of the diffused orbital than the solid-body approximations:
real orbitals
(linear combination)
(see for instance this Wikipedia page). A great piece of code is provided by Jacopo Bertolotti:
\[Alpha]0 = 1; \[Psi][n_, l_, m_, r_, \[Theta]_, \[Phi]_] := Sqrt[(2/(n \[Alpha]0))^3 (n - l - 1)!/(2 n ((n + l)!))] E^(-r/(n \[Alpha]0)) ((2 r)/(n \[Alpha]0))^l LaguerreL[n - l - 1, 2 l + 1, (2 r)/(n \[Alpha]0)] SphericalHarmonicY[l, m, \[Theta], \[Phi]]; p1 = Flatten@Table[ f = TransformedField["Spherical" -> "Cartesian", \[Psi][n, l, m, r, \[Theta], \[Phi]], {r, \[Theta], \[Phi]} -> {x, y, z}]; DensityPlot3D[Abs[f]^2 , {x, -30, 30}, {y, -30, 30}, {z, -30, 30}, ColorFunction -> Hue, ColorFunctionScaling -> True, Boxed -> False, Axes -> False, PlotLabel -> Style[StringForm["Hydrogen atom orbitals\n |\[Psi]\!\(\*SuperscriptBox[\(|\), \\(2\)]\) : n=`` l=`` m=``", n, l, m], Medium, FontFamily -> "DejaVu Serif"], LabelStyle -> {Black, Bold}, RegionFunction -> Function[{x, y, z}, x < 0 || y > 0], PlotLegends -> Automatic], {n, 1, 4}, {l, 0, n - 1}, {m, -l, l}]
orbitals of multi-electron atoms are qualitatively similar to those of hydrogen
Links
- The grand orbital table, the most complete orbital table available.
- The orbitron.
- Applet.
- Paper in J. Comput. Chem. Jpn., Vol. 5, No. 3, pp. 159–164 (2006).