Complete Set of Commuting Observables

(Part of the Wolverhampton Lectures of Physics's Quantum Physics Course)

The problem of representing the state of a dynamical system is interesting also in classical physics, where the notation of phase-space brings us to some abstract universe not directly palpable to our sense but which simplifies a lot the behavior of a system. A harmonic oscillator, for instance, should not be looked at in the real space, where it has fancy oscillations, but in the $(x,p)$ space where it becomes a closed ellipse and where one can study much better its stability and overall dynamics. But in quantum mechanics, we hit right away the problem of Heisenberg's uncertainty principle: one measurement may affect the system as to leave it completely undetermined for another measurement. The famous as well as historical example that illustrates this, is position/momentum, precisely the axes of our classical phase-space: if you look where the quantum object is, you don't know which speed it is going at! (and vice-versa, if you know its speed, you don't know where it is). Therefore, we can forget about tracking it in this way (this is still doable and brings us to other formulations of the theory, such as the so-called Wigner representation which we will see in WLP_XVI/Electrodynamics).

Last year, we have learned—and in the previous Lectures, we have reminded ourselves—how to solve the Schrödinger equation by finding a set of eigenstates for the Hamiltonian and corresponding eigenvalues (energies). Now that we have more dimensions, i.e., more degrees of freedom. We need to also find a good set of observables to express the added degrees of freedom, without one observable messing up the others, like position/momentum, in which case we say that the observables are incompatible. They cannot be used together. Energy will typically always be one of the observables we want, but it is not energy alone anymore and we must find compatible observables to complete our description of the states. Depending on the problem, certain sets are more relevant or meaningful than others. For the 2D harmonic oscillator, that we will use as an example, it could be, e.g., the number of excitations in the $x$ and $y$ direction (note, that's two numbers, like the number of dimensions) or it could be more elegant and/or insightful to use angular momentum, as we discussed last time.

Let us start today where we started initially and label the states of the Harmonic oscillators with $n_x$ and $n_y$, the number of quanta of excitations in the $x$ and $y$ directions, respectively. The quantum state in Dirac notation is then written as

$$|n_x,n_u\rangle\,.$$

This state is characterized by the observables $\hat n_x\equiv a_x^\dagger a_x$ and $\hat n_y\equiv a_y^\dagger a_y$ in the sense that if we measure these quantities, the state remains what it is: $|n_x,n_u\rangle$. In particular, this allows us to measure first $n_x$ and then $n_y$ or vice-versa, so the measurement is consistent and stable, and we can be confident of what we have.

Say that our system is in the state $|n_x=3,n_y=2\rangle$. Then, by measuring how many excitations we have along $x$, that is, applying $a_x^\dagger a_x$ to the state, since it is an eigenstate, i.e., $a_x^\dagger a_x|3,2\rangle=3|3,2\rangle$, according to the postulates of quantum mechanics, we have collapsed our state on $|3,2\rangle$ and measured $n_x=3$. Note that we collapsed the state onto itself, thereby not changing it! We didn't affect neither $x$ nor $y$. The perfect measurement: we get information without perturbing the system. This is called a good quantum number. The same applies with $a_y^\dagger a_y$ with $a_y^\dagger a_y|3,2\rangle=2|3,2\rangle$, so we can be confident that we have:

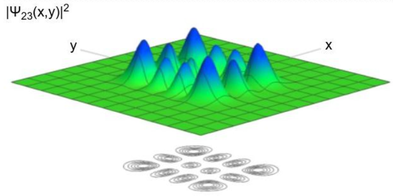
We have drawn the wavefunction in space. This is not what we would see, or measure, this is what we have. Would we measure the wavefunction in space, it would collapse to a point—where we find the particle—and not have a well-defined number of excitations along $x$ and $y$ anymore.

Say that we want to make such a position measurement along the $x$ axis. Since $|3,2\rangle$ is not an eigenstate of the operator $\displaystyle\hat x={1\over\sqrt{2}\beta}(a_x+a_x^\dagger)$ (cf. tutorial), an indeterminate outcome will be obtained and the state will be left (collapsed) to where we found it, namely, on one eigenstate of the $\hat x$ operator, which looks very different from the Hermite polynomials, as it is a Dirac delta function. We can only know, in this scenario, the probability to find it somewhere, namely, according to the distribution of $|\psi_{3}(x)|^2$. We are not doing anything with $y$ in this case, thus this won't be affected by our measurement of $x$ and we obtain $\psi_3$ either from our knowledge of the $1D$ case or by averaging over the $y$ dimension:

$$|\psi_3(x)|^2=\int_{-\infty}^\infty|\psi_{3,2}(x,y)|^2\,dy\,.$$

The point that is randomly sampled in $x$ becomes, post-measurement, the initial condition for the Schrödinger equation. Since the position is exact, that results in an infinite speed. A big mess we made! Position is not a good quantum number. Quantum mechanics usually does not describe states by "where they are" (this is classical thinking) but, in this case, how many quata they store in each direction.

We said that energy is important and typically one degree of freedom we want to label our states with. We already have enough good quantum numbers, $n_x$ and $n_y$. Energy could, however, be also one of them, or, to avoid redundancies, supplement one of them, since energy is $E=(n_x+n_y)\hbar\omega$. So we could label the state exactly and completely with, e.g., $E$ and $n_x$ (or $n_y$, but only one is needed).

Since we start to have a collection of observables, let us now look at angular momentum $L_z$ for the state $|3,2\rangle$. This will bring up the same problematic without going to such extremes of exact positions and infinite speed. Indeed, $|3,2\rangle$ is not, either, an eigenstate of $a_d\dagger a_d$ or $a_g\dagger a_g$, the number of quanta of rotation (cf. tutorial). Say we want to know how much the oscillator is rotating clockwise ($d$) or anticlockwise ($g$), then, according to the postulates of quantum mechanics, we need to write the state in the basis of the rotation operators. From the last lecture's definitions

\begin{align} a_d&={1\over\sqrt{2}}\left(a_x-ia_y\right)\\ a_g&={1\over\sqrt{2}}\left(a_x+ia_y\right) \end{align}

one can readily obtain the inverse relations:

\begin{align} a_x&={1\over\sqrt{2}}\left(a_d+a_g\right)\\ a_y&={i\over\sqrt{2}}\left(a_d-a_g\right) \end{align}

So that $|3,2\rangle=a_x^{\dagger3}a_y^{\dagger 2}|0,0\rangle/\sqrt{3!2!}$ can be calculated in the new basis. Usually, which basis one is using is clear from context, but to make sure we will append $x,y$ subscripts for the Cartesian basis:

$$|3_x,2_y\rangle=a_x^{\dagger3}a_y^{\dagger 2}|0_x,0_y\rangle/\sqrt{3!2!}$$

so that we can now compute:

\begin{align} \sqrt{3!2!}|3,2\rangle&=\left({1\over\sqrt{2}}(a_d^\dagger+a_g^\dagger)\right)^3\left({-i\over\sqrt{2}}(a_d^\dagger-a_g^\dagger)\right)^2|0,0\rangle\\ &=-{1\over 2^{3/2}}(a_d^{\dagger3}+3a_d^{\dagger 2}a_g^\dagger+3a_d^\dagger a_g^{\dagger2}+a_g^{\dagger3})(a_d^{\dagger2}-2a_d^\dagger a_g^\dagger+a_g^{\dagger2})|0,0\rangle \end{align}

which, putting the normalization constant on the same side (and labelling $x,y$ the lhs, but not $d,g$ the rhs unless absolutely necessary):

$$|3_x,2_y\rangle=-{1\over 2^{5/2}\sqrt{3!2!}}(\sqrt{5!}|5,0\rangle+\sqrt{4!}|4,1\rangle-2\sqrt{3!2!}|3,2\rangle-2\sqrt{3!2!}|2,3\rangle+\sqrt{4!}|1,4\rangle+\sqrt{5!}|0,5\rangle)\,.$$

You can check that the state is properly normalized (384/same). Thus we can find the state to be rotating completely clockwise or completely anticlockwise with probability $5/8$ ($5/16$ each), and to have a mixture of both components of $3/8$ (with $1/8$ one vs four quanta and $1/4$ to have two vs three, one way or the other). The most likely is thus to share the rotation as equally as possible.

Say we find $|3_d,2_g\rangle$, it is, then the state has collapsed on that. Further measurements of the rotation will, once there, always return $3_d$ and $2_g$. But, if measuring back in the $x$, $y$ basis again, this will probably not bring us back to $|3_x,2_y\rangle$ again (cf. tutorial for the quantitative meaning of "probably" here). Therefore, $x,y$ and $d,g$ are not compatible.

While cartesian and polar coordinates are not compatible, note that energy is always conserved, namely, it will always be $(n_x+n_y+1)\hbar\omega$ or $(n_d+n_g+1)\hbar\omega$ which is $6\hbar\omega$ in the current case. The two bases are not compatible but they all offer good quantum numbers. They both could work, depending on one's personal approach and/or interest.

So what makes a good choice of observables? Well, clearly, they need to have common eigenstates, so that we do not scramble the state we start with through the postulates of quantum mechanics when we look at the possibilities that could arise. Indeed, energy and $x$, $y$ oscillations as well as $d$ & $g$ rotations have common eigenstates. Besides, we know that Hermitian operators have eigenstates that span the Hilbert space, i.e., their eigenvectors provide a basis for the space. We call that "completeness", they describe all the possible outcomes. The question becomes, how do we know, then, that operators share a basis of eigenstates? This is actually easy and forms the main result of this lecture:

$A$ and $B$ are compatible observables iff $A$ and $B$ commute.

This is easy to check for the $x,y$ and $d,g$ operators with $H$, which is a sum of them:

$$H=(a_x^\dagger a_x+a_y^\dagger a_y+1)\hbar\omega=(a_d^\dagger a_d+a_g^\dagger a_g+1)\hbar\omega\,.$$

That also shows right away that the two bases are not compatibles or that position is not compatible with energy:

$$\begin{align} [x,H]&={\hbar\omega\over\sqrt{2}\beta}[a_x+a_x^\dagger,a_x^\dagger a_x+a_y^\dagger a_y]\\ &={\hbar\omega\over\sqrt{2}\beta}\left([a_x,a_x^\dagger a_x]+[a_x^\dagger,a_x^\dagger a_x]\right)\\ &={\hbar\omega\over\sqrt{2}\beta}\left(a_x-a_x^\dagger\right) \end{align}$$

To prove the statement in its full generality is not much more difficult, at least for the gist of it:

• Compatible observables commute: let's call $|\psi_n\rangle$ the common eigenkets of $A$ and $B$ (that's what it means for them to be compatible). Then $AB|\psi_n\rangle=A\beta_n|\psi_n\rangle=\beta_n A|\psi_n\rangle=\beta_n\alpha_n|\psi_n\rangle$ with $\alpha_n, \beta_n$ the corresponding eigenvalues (doesn't matter what they are). Similarly, $BA|\psi_n\rangle=\beta_n\alpha_n|\psi_n\rangle$ since $\alpha_n$ and $\beta_n$ commute (they're scalars, not operators). Therefore, for all $|\psi_n\rangle$, $[A,B]|\psi_n\rangle=0$ but since $|\psi_n\rangle$ form a basis of the space, this is true for any vector of the space obtained as a linear superposition of basis vectors. If it's true for all vectors, then it's true at the operator level, and thus $[A,B]=0$, QED.
• Commuting observables share a basis of eigenvectors: $A$ is Hermitan, so we know it has a complete set of eigenstates $|\psi_n\rangle$ with eigenvalues $\alpha_n$. We need to prove they are also eigenstates of $B$ if $A$ and $B$ commute. It's trivially proved if we assume eigenstates are non-degenerate: $AB|\psi_n\rangle=BA|\psi_n\rangle=B\alpha_n|\psi_n\rangle=\alpha_n B|\psi_n\rangle$ so $B|\psi_n\rangle$ is an eigenstate of $A$ with eigenvalue $\alpha_n$. Since we assumed there is no degeneracy, $B|\psi_n\rangle\propto|\psi_n\rangle$ (since there is only one eigenvector corresponding to this eigenvalue). But that is the definition of $|\psi_n\rangle$ being an eigenstate of $B$. This is true for all eigenstates, hence the result for non-degenerate cases.

In quantum mechanics, the degenerate case always brings in some complications and heavier maths. The proof for the degenerate case follows in spirit the trivial one above, but uses, in addition, the closure of polynomial equations, i.e., that roots of polynomials always exist, even if they cannot be expressed in closed form. The proof thus shows that solutions exist without, if degeneracy is higher than 5, being able to actually provide it: a very-mathematical result:

• Commuting observables share a basis of eigenvectors (general proof): Let us call $\alpha_n$ the $n$th eigenvalues of $A$ which is $g$-degenerate, i.e., there are $g$ eigenvectors $|\psi_{nr}\rangle$ for $1\le r\le g$ such that $A|\psi_{nr}\rangle=\alpha_n|\psi_{nr}\rangle$. From the same reasoning as above, $B|\psi_{nr}\rangle$ is an eigenstate of $A$ with eigenvalue $\alpha_n$, i.e., there exists $c_{rs}$ coefficients such that $B|\psi_{nr}\rangle=\sum_s c^{(n)}_{rs}|\psi_{ns}\rangle$. This is at this stage that the proof differs, because the right-hand side being a linear combination of eigenvectors of $A$, it is not immediate that it is directly an eigenvector of $B$ too. Also, we kept $n$ explicit throughout so that it's clear that we can deal like this with all the eigenvalues. We must find the $c_{rs}$ that make it work. To do so, we now make a linear superposition of $B|\psi_{nr}\rangle$ with as yet general coefficients in the hope of finding a good balance:

$$\displaystyle\sum_{r=1}^g d_rB|\psi_{nr}\rangle=\sum_{r=1}^g d_r \sum_{s=1}^gc_{rs}^{(n)}|\psi_{ns}\rangle\,.$$

We can find this good balance by commuting the sums on the right-hand side, factoring $B$ on the left-hand side and using a different dummy index for higher clarity between both sides of the equation:

$$B\displaystyle\sum_{s=1}^g d_s|\psi_{ns}\rangle=\sum_{s=1}^g\left(\sum_{r=1}^g d_r c_{rs}^{(n)}\right)|\psi_{ns}\rangle$$

taking good notice that the sum in parenthesis is standalone. If we could demand this sum to satisfy:

$$\forall s\in[\![1,g]\!],\quad\displaystyle\sum_{r=1}^g d_r c_{rs}^{(n)}=b_nd_s$$

then we'd be done as we would have $B\displaystyle\sum_{s=1}^g d_s|\psi_{ns}\rangle=b_n\sum_{s=1}^gd_s|\psi_{ns}\rangle$ meaning that $\sum_{s=1}^g d_s|\psi_{ns}\rangle$ is an eigenstate of $B$ with eigenvalue $b_n$. We must show that this possible and also, that we can do that $g$ times, since we must do it for all $s$, that is, for each eigenvector of $A$. This is the easiest part of the proof since this relies on the fundamental theorem of calculus, which says that the equation above always has solutions. We can see that by writing all the $s$ equations simultaneously as a matrix equation:

$$\begin{pmatrix}\\&&c_{rs}^{(n)}&&\\&\end{pmatrix} \begin{pmatrix}d_1\\\vdots\\d_s\end{pmatrix} =\beta_n \begin{pmatrix}d_1\\\vdots\\d_s\end{pmatrix}\,.$$

This is precisely an eigenvalue problem. It has solutions provided that $\det{(C-\beta_n\mathbb{1})}=0$ calling $C$ the matrix of $c_{rs}^{(n)}$. The characteristic polynomial is of order $g$ in the variable $\beta_n$, for which one can find (fundamental theorem) $g$ complex-valued solutions (possibly degenerate, or not). These solutions are the eigenvalues of $B$ and the eigenvectors are the coefficients to build the corresponding $B$ eigenvectors that share their eigenvalues with $A$. QED.

So now we know, and have proven, how to pick up (or identify) a so-called complete set of commuting observables (CSCO): this is a set of commuting Hermitian operators. Being Hermitian, their eigenvalues completely specify the state of the system. Again: it is complete because it describes fully the state (in 3D for instance we would need three observables, as we will see with the hydrogen atom). It is commuting so that their measurements can be performed simultaneously and in any order without affecting each other. If they don't, then Heisenberg's uncertainty principle will prevent the common knowledge and we thus do not characterize the state.

We conclude with a final aesthetic touch: instead of $n_x, n_y$ or $n_d, n_g$ in addition to the energy (their sum), we can go for something more physical in the form of the total angular momentum, which we remind from last lecture, is their difference $L_z=\hbar(a_d^\dagger a_d-a_g^\dagger a_g)$. It is easy to check that $[L_z,H]=0$, so while position and momentum are not compatible with energy, angular momentum is. We can know both (simultaneously) the energy and the angular momentum of the state. So a better "labeling" of the states of the 2D oscillator, rather than $|n_x,n_y\rangle$ or $|n_d,n_g\rangle$ is actually

$$|n,m\rangle$$

where

$$n\equiv n_d+n_g\quad\text{and}\quad m\equiv n_d-n_g$$

so that the classification goes:

$$\begin{align*} n&=0\,, &m=0&\,,\\ n&=1\,, &\begin{cases} m=&-1\\ m=&1 \end{cases}\,,\\ n&=2\,, &\begin{cases} m=&-1\\ m&=0\\ m=&1 \end{cases}\,, \end{align*}$$

Of course the state $|n,m\rangle$ is obtained as $\displaystyle \left(a_d^{\dagger}\right)^{n+m\over2}\left(a_g^{\dagger}\right)^{n-m\over2}|0,0\rangle$, which we know how to build from the previous lecture.