Hydrogen wavefunctions

Orbitals of multi-electron atoms are qualitatively similar to those of hydrogen

Now that we have the closed-form analytical expressions for the Hydrogen wavefunctions, namely:

$${\displaystyle \psi _{n\ell m}(r,\theta ,\varphi )={\sqrt {{\left({\frac {2}{na_{0}^{*}}}\right)}^{3}{\frac {(n-\ell -1)!}{2n(n+\ell )!}}}}e^{-\rho /2}\rho ^{\ell }L_{n-\ell -1}^{2\ell +1}(\rho )Y_{\ell }^{m}(\theta ,\varphi )}$$

(where $\rho=2r/(na_\mathrm{B})$, $L$ are Laguerre polynomials $Y$ spherical harmonics) we can turn to the problem of their visualisation.

The orbitals represent the probability density function to find the electron according to the postulate of quantum mechanics. At such, they can be understood as a description of a diffuse electron cloud in a standing wave pinned to its nucleus.

They extend to much extent to all atoms, as we shall see in the coming lectures, where they are called "atomic orbitals". For hydrogen, the stationary orbitals are specified by three quantum numbers:

$$n,\quad l\quad\text{and}\quad m$$

• The number $n$ or principal quantum number can take any positive integer value, $n=1, 2, \cdots$. It describes the energy and also the average distance of the electron from the nucleus, thus, qualitatively, its size. Orbitals with the same $n$ are, for this reason, collectively described as belonging to the same "shell". It already appears in the Bohr model.

• The number $l$, or azimuthal quantum number, describes the rotation, or angular momentum, of the electron. It describes, qualitatively, the shape of the orbital. It is an integer, possibly and always at least zero, otherwise strictly bounded by the principal quantum number: $0\le l\le n-1$. The orbitals with the same $n$ and $l$ are called "subshells". They are denoted $s$ (sharp) for $l=0$, $p$ (principal) for $l=1$, $d$ (diffuse) for $l=2$ and $f$ (fundamental) for $l=3$ due to historical reasons (?!) and proceed beyond that alphabetically at the exception of j which is skipped: $g, h, i, k, l, \cdots$ This gives rise to naming such as 1s ($n=1, l=0$, i.e., the ground state) or $2p$ ($n=2$, $l=1$).

• The number $m$, or magnetic quantum number, can take negative values, and is bounded in absolute value by $l$: $-l\le m\le l$. It describes, qualitatively, the orientation of the orbital.

The $s$ subshells are shaped like spheres, with the ground state being simply a fading ball. Higher $n$ with $l=0$ have radial (spherical) symmetry but with oscillations due to destructive interferences. The $s$ orbitals are the only ones with an antinode at the centre (where the nucleus is) while other orbitals present a node there. This does not invalidate the model, though, as the probability for the electron to be actually found there remain negligible.

There are three $p$-orbitals (starting at $n=2$) corresponding to $m=\pm1$ and 0. They each have the form of two ellipsoids pointing in opposite directions and pinned by a node at the nucleus, and are otherwise perpendicularly oriented the ones from the others, which one can align with the Cartesian axis vectors $\hat\imath$, $\hat\jmath$ and $\hat k$.

There are five $d$-orbitals (starting at $n=3$) corresponding to $m=\pm2, \pm1$ and 0.

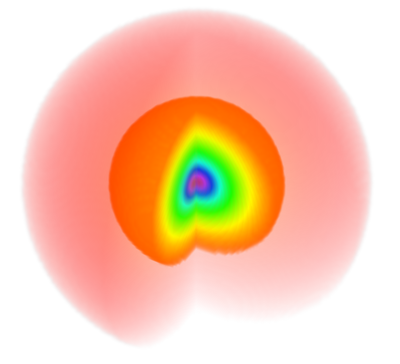
The color code is such that yellowish-orangeish-redish colors fade into zero and blueish-purplish or (confusingly, extremely red) colors peak into the highest values (see it here exactly for $\psi_{100}$)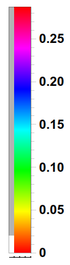

In contrast to the real-valued orbitals in chemistry, which are superpositions of several m-eigenstates, the probability densities shown here are symmetric around the z-axis.

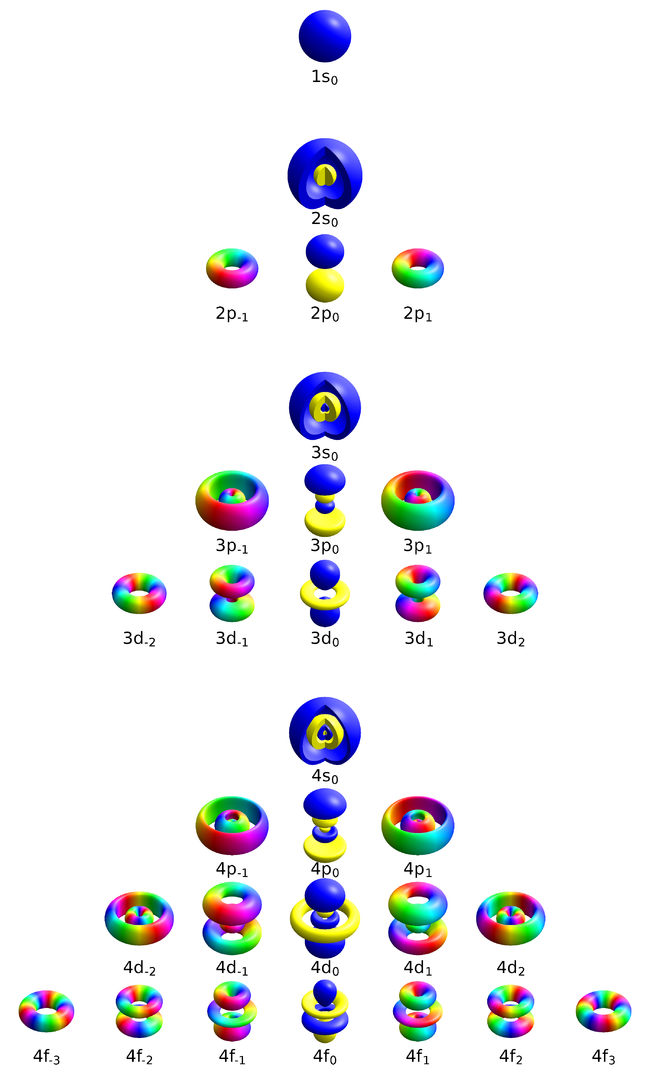
This representation [1]—from Geek3—shows solid bodies that enclose a volume of space where the probability density exceeds a threshold that has been chosen to produce nice-looking results. The color depicts the phase of the complex-valued wavefunction at the corresponding point. The 2s, 3s and 4s orbitals are cut open to reveal the inner structure. The wavefunctions are in the basis or orbitals that are symmetric around the $z$ axis. This representation finds over variations here.

This representation [2], also by Geek3, uses transparency and 3D rendering of the with the colour depicting the sign of $\psi$. The cloud gives a more realistic representation of the diffused orbital than the solid-body approximations:

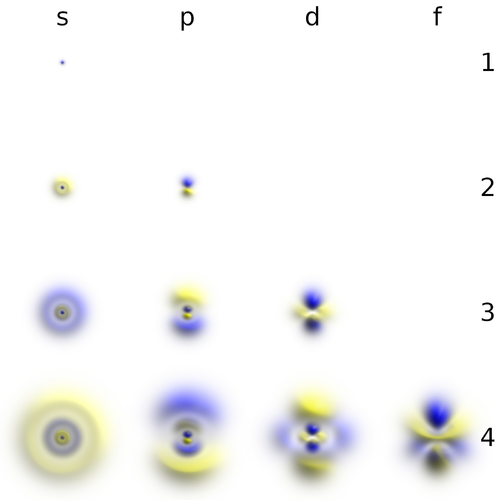
real orbitals

(linear combination)

(see for instance this Wikipedia page). A great piece of code is provided by Jacopo Bertolotti:

\[Alpha]0 = 1;
\[Psi][n_, l_, m_, r_, \[Theta]_, \[Phi]_] := Sqrt[(2/(n \[Alpha]0))^3 (n - l - 1)!/(2 n ((n + l)!))] E^(-r/(n \[Alpha]0)) ((2 r)/(n \[Alpha]0))^l LaguerreL[n - l - 1, 2 l + 1, (2 r)/(n \[Alpha]0)] SphericalHarmonicY[l, m, \[Theta], \[Phi]];
p1 = Flatten@Table[
   f = TransformedField["Spherical" -> "Cartesian", \[Psi][n, l, m, r, \[Theta], \[Phi]], {r, \[Theta], \[Phi]} -> {x, y, z}];
   DensityPlot3D[Abs[f]^2
    , {x, -30, 30}, {y, -30, 30}, {z, -30, 30}, ColorFunction -> Hue, ColorFunctionScaling -> True, Boxed -> False, Axes -> False, PlotLabel -> Style[StringForm["Hydrogen atom orbitals\n |\[Psi]\!\(\*SuperscriptBox[\(|\), \\(2\)]\) : n=`` l=`` m=``", n, l, m], Medium, FontFamily -> "DejaVu Serif"], LabelStyle -> {Black, Bold}, RegionFunction -> Function[{x, y, z}, x < 0 || y > 0], PlotLegends -> Automatic], {n, 1, 4}, {l, 0, n - 1}, {m, -l, l}]

Links

• The grand orbital table, the most complete orbital table available.
• The orbitron.
• Applet.
• Paper in J. Comput. Chem. Jpn., Vol. 5, No. 3, pp. 159–164 (2006).