Crash Course in Scientific Computing

III. Computer Programming

Computers are good at computing! We have seen various definitions of Euler's number $e$, of which, in particular:

$$\tag{1}e=\lim_{n\rightarrow\infty}\left(1+{1\over n}\right)^n$$

$$\tag{2}e=\sum_{k=0}^\infty{1\over k !}$$

A computer would make a great job of checking this, in particular when convergence is slow. It will also allow us to deepen this important business of convergence.

Let us compute (1): for $n=1$, this is $(1+(1/1))=2$. For $n=2$, this is $(1+(1/2))^2=9/4=2.25$. For $n=3$, this is $(1+(1/3))^3=(4/3)^3=64/27=2.\overline{370}$. Unlike computers, we get pretty tired. So we can ask the computer to do it. This is how one popular computer program, Wolfram's Mathematica, would do it:

Table[N[(1 + 1/n)^n], {n, 1, 10}]
{2., 2.25, 2.37037, 2.44141, 2.48832, 2.52163, 2.5465, 2.56578, \
2.58117, 2.59374}

It is, literally, just doing the same as we've been doing, except that it did that in 0.000041s. The command N[] in Mathematica means "numerical", since this is a symbolic program that can do both numerical (as we mainly will during this course) as well as symbolic calculations.

Back to our business: does this converge to $e\approx 2.71828$? If so, very slowly. Let us check with more points:

Table[N[(1 + 1/n)^n], {n, 1, 100}]
{2., 2.25, 2.37037, 2.44141, 2.48832, 2.52163, 2.5465, 2.56578, \
2.58117, 2.59374, 2.6042, 2.61304, 2.6206, 2.62715, 2.63288, 2.63793, \
2.64241, 2.64643, 2.65003, 2.6533, 2.65626, 2.65897, 2.66145, \
2.66373, 2.66584, 2.66778, 2.66959, 2.67128, 2.67285, 2.67432, \
2.6757, 2.67699, 2.67821, 2.67936, 2.68044, 2.68146, 2.68244, \
2.68336, 2.68423, 2.68506, 2.68586, 2.68661, 2.68733, 2.68802, \
2.68868, 2.68931, 2.68992, 2.6905, 2.69105, 2.69159, 2.6921, 2.6926, \
2.69307, 2.69353, 2.69398, 2.6944, 2.69481, 2.69521, 2.6956, 2.69597, \
2.69633, 2.69668, 2.69702, 2.69734, 2.69766, 2.69797, 2.69827, \
2.69856, 2.69884, 2.69912, 2.69938, 2.69964, 2.69989, 2.70014, \
2.70038, 2.70061, 2.70084, 2.70106, 2.70127, 2.70148, 2.70169, \
2.70189, 2.70209, 2.70228, 2.70246, 2.70264, 2.70282, 2.703, 2.70317, \
2.70333, 2.7035, 2.70365, 2.70381, 2.70396, 2.70411, 2.70426, 2.7044, \
2.70454, 2.70468, 2.70481}

This time it took 0.000449s, so still fast enough, but even the 100th number doesn't get us quite there, the 2nd decimal is still off! We can get a sense of what the computer computes by plotting it. A picture is worth a hundred numbers!

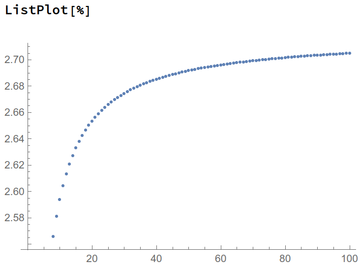
The fact that the curve still evolves (it is not horizontal), although slowly, shows that the calculation is not over. We don't have to compute all the terms though, only to take $n$ large enough, so let us see what we get with:

N[(1 + 1/1000)^1000]
2.71692

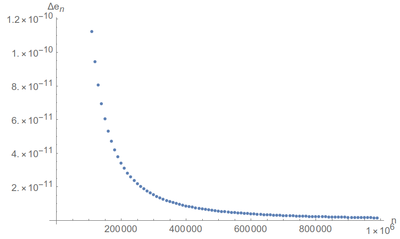
Ah ah! Well, the 2nd decimal is correct, but not the third. If we zoom as we compute, we see that convergence remains very slow:

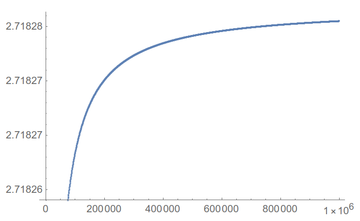
One needs $n$ as large as 743325 for a nice-looking result on screen:

A nice computer problem: which value of $n$ do we need to take so that the displayed value of $e$, i.e., to 5 decimal places, be the correct (theoretical) one? (Answer)

Let us compare with the other method, Eq. (2), which looks much more complicated since it involves a sum! for $n=1$, this is 1+1=2, the same value as before but with a sum of two. For $n=2$, this is $2+1/2=2.5$, so quite better (compare with 2.25), for $n=3$, $2.5+1/6=2.\bar 6$, so this time clearly much better (compare with 2.37 which is even worse than the $n=2$ approximation). In fact, while we needed $n=743325$ with Eq. (1), we get there with $n=8$ only using Eq. (2):

Show that $\sum_{k=0}^8(1/k!)=109\,601/40\,320=2.7182787\overline{698412}$.

Up to $n=8$ one could still compute by hand, but this becomes tedious. For a computer this is piece of cake:

le2 = Table[{n, Sum[1/k!, {k, 0, n}]}, {n, 1, 10}]
{{1, 2.}, {2, 2.5}, {3, 2.66667}, {4, 2.70833}, {5, 2.71667}, {6, 2.71806},
 {7, 2.71825}, {8, 2.71828}, {9, 2.71828}, {10, 2.71828}}

and indeed we don't see the difference, on screen. We can pass an option to Mathematica's N[] command, so that it computes to higher decimal places, including beyond machine precision, which is the maximum number that fits in the computer in native form. Let us see the result up to 25 decimal places:

le2 = Table[{n, N[Sum[1/k!, {k, 0, n}], 25]}, {n, 1, 10}]
{{1, 2.000000000000000000000000}, {2, 2.500000000000000000000000}, 
 {3, 2.666666666666666666666667}, {4, 2.708333333333333333333333}, 
 {5, 2.716666666666666666666667}, {6, 2.718055555555555555555556}, 
 {7, 2.718253968253968253968254}, {8, 2.718278769841269841269841}, 
 {9, 2.718281525573192239858907}, {10, 2.718281801146384479717813}}

as compared to:

N[E, 25]
2.718281828459045235360287

(E is $e$ in Mathematica language). Remembering that graphs show us the big picture, we can compare the convergence with this method:

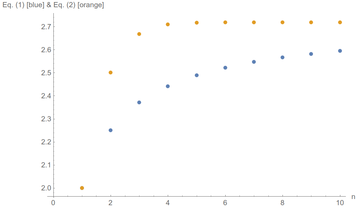
That shows that the sum is actually much more efficient. The curve quickly plateaus, we say that the result has converged and we can take it as stable with no need of further calculation.

A nice and standard way to check convergence is to compute the difference of successive terms. The speed at which this goes to zero tells us how efficient or good is the convergence (if this doesn't go to zero, then it clearly doesn't converge as the results do not tend towards a unique value). This graph should convince you that one method is much faster than the other:

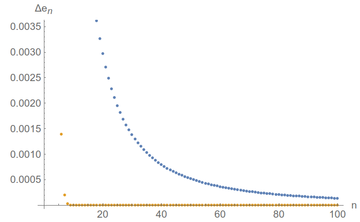
The sum of inverse factorials is so fast that we quickly lose track of its uncertainty. Convergence! We can keep an eye on it by plotting in log-scale, which means that we label our axes (only the $y$ axis in this case) not linearly but as a logarithm so that exponentials (i.e., quick changes) become line (smooth changes). If we do that, we see that convergence is very good indeed ($10^{-120}$ is a very small number) and that the single-term approximation, Eq. (1), in blue, is basically stuck:

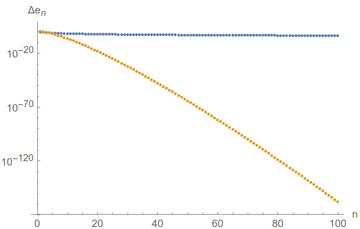
Don't get it wrong: the blue curve is also going to zero... just very slowly!

It will be a recurrent theme of the course to find out efficient numerical methods, so that we get good results quickly, involving a few resources and small numbers!

Let us turn to another nice problem involving similar calculations, namely, the Fibonacci sequence, that is formed by computing each number of the list by summing the two previous ones, $F_{n}=F_{n-1}+F_{n-2}$, starting with (for the official Fibonacci) $F_0=0$ and $F_1=1$. Clearly we have $F_2=0+1=1$, $F_3=1+1=2$, $F_4=1+2=3$, $F_5=2+3=5$, so on and so forth. The sequence thus starts:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...

There is an encyclopedia of such integer sequences, the On-Line Encyclopedia of Integer Sequences (OEIS), which is one of the examples of good use of the Internet. There the Fibonacci appears as A000045. Read about it.

History of Science tells us that this sequence arises from a problem involving a proliferation of rabbits, a recurrent theme in mathematical modelling, which Fibonacci himself describes in 1202 in his master opus, the Liber Abaci (a book to introduce the decimal system) by asking how many pairs of rabbits are there in subsequent months given that each pair needs one month to mature and give offspring but otherwise generate one pair every month. No rabbits die. Such a simple problem can be shown by proper bookkeeping to have the solution of the sequence above. There are techniques to find a closed-form solution, but the computer would solve this readily. Or would it? Let us look at this particular implementation:

f[0]=0
f[1]=1
f[n_]:=f[n - 1] + f[n - 2]

There is a bit of syntax issues here. Mathematica requires an underscore to signify that the variable can be expanded. For us this is a detail, what we care about is that, our code indeed gives the good result:

f[5] // Timing
{0.000052, 8}

that match with Sloane's series above:

f[12] // Timing
{0.001443, 144}

but if you have a keen eye (and are good at following cues, we're not looking at the time for nothing), you'll notice something odd is going on. Let us expand on the sequence, keeping track of the times:

fib = Table[f[i] // Timing, {i, 0, 30}]
{{9.*10^-6, 0}, {2.*10^-6, 1}, {7.*10^-6, 1}, {4.*10^-6, 
  2}, {6.*10^-6, 3}, {8.*10^-6, 5}, {0.000014, 8}, {0.000024, 
  13}, {0.000036, 21}, {0.000059, 34}, {0.000096, 55}, {0.000153, 
  89}, {0.000284, 144}, {0.000431, 233}, {0.000667, 377}, {0.001141, 
  610}, {0.002197, 987}, {0.004954, 1597}, {0.006706, 2584}, {0.00735,
   4181}, {0.011941, 6765}, {0.019106, 10946}, {0.031253, 
  17711}, {0.049779, 28657}, {0.081837, 46368}, {0.129615, 
  75025}, {0.210993, 121393}, {0.339594, 196418}, {0.548714, 
  317811}, {0.893796, 514229}, {1.45974, 832040}}

So okay, the 30th number is $F_{30}=832\,040$ obtained as $F_{29}+F_{28}=514\,229+317\,811$. But note that it took the computer a whole 1.46s to get that... which the fastest people out there would be able to compute in less time than that. If you think you're too slow, then go for $F_{40}$, which takes 204.144ss (that is 3m24s) for the computer and time yourself, that's:

$$\tag{3}F_{40}=39\,088\,169+63\,245\,986\,.$$

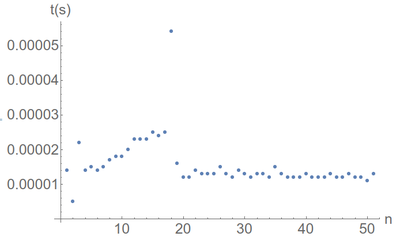
We're speaking of millions, but not something that cannot be done by any school kid. If it still takes you a few minutes to write it down and you struggle with adding all these 8 and 9, try $F_{42}=F_{41}+F_{40}=165\,580\,141+102\,334\,155$, which involves easier (smaller) numbers and now takes a whole 564s for the computer (almost 10min)! Here's how the time scales with the increasing Fibonacci numbers:

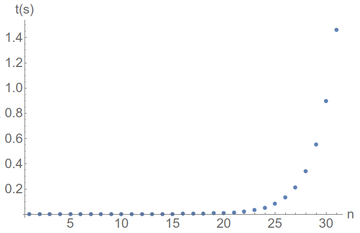
Again, we get a better view by looking with a proper scale for the phenomenon:

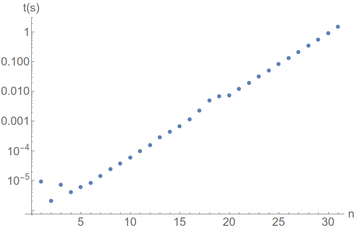
Since when are we able to compute faster than a computer?

Note that if you ask the computer to go for Eq. (3) directly, sure enough, it does that in a few ms (0.00001s on wulfrun2 so probably below timing precision) and the same for the other example. So what is going on? The reason is very simple... and is one of the most dangerous pitfalls when instructing a computer: to have it do the job, but in a very inefficient, redundant and wasteful way. What's going on here, is that when we ask it to compute the sequence by involving over and over the same function, which is called "recursively" by the way, the computer goes as follows, say for

$$\begin{align} F_7&=F_6+F_5\\ &=F_5+F_4+F_4+F_3\\ &=F_4+F_3+F_3+F_2+F_3+F_2+F_2+F_1\\ &=F_3+F_2+F_2+F_1+F_2+F_1+F_1+F_0+F_2+F_1+F_1+F_0+F_1+F_0+F_1\\ &=F_2+F_1+F_1+F_0+F_1+F_0+F_1+F_1+F_0+F_1+F_1+F_0+F_1+F_0+F_1+F_1+F_0+F_1+F_0+F_1\\ &=F_1+F_0+F_1+F_1+F_0+F_1+F_0+F_1+F_1+F_0+F_1+F_1+F_0+F_1+F_0+F_1+F_1+F_0+F_1+F_0+F_1\\ &=1+0+1+1+0+1+0+1+1+0+1+1+0+1+0+1+1+0+1+0+1\\ &=13 \end{align}$$

and this is a lot of work to merely compute 5+8. So keep in mind: the computer is stupid! This is for you to do the thinking, and make it understand it doesn't need to compute over and over and over again the same thing, in this case, for instance, computing eight times $F_2$. A single time would suffice! This big problem that means that $F_{100}$ obtained in this blunt recursive way is probably out of reach of any computer, is readily removed by one innocent-looking correction, that brings back an impossible calculation into a matter of milliseconds:

f[n_] := f[n] = f[n - 1] + f[n - 2]

What we now ask the computer to do is to store in memory the result of its calculation, so that when we ask it f[n], it doesn't compute it each time, thus triggering a whole new chain of recursive calculations which will by themselves also call for more recursive calculations, resulting in this exponential slow-down, but it will check if it has it already, if not, computes it, if yes, use it straight-away. Doing it this way brings back the computing time to something normal-looking:

Hofstadter sequences are a family of nonlinear recurrence relations. The following are interesting:

The $G$ sequence: \begin{align} G(0)&=0 \\ G(n)&=n-G(G(n-1)), \quad n>0. \end{align}

The $H$ sequence: \begin{align} H(0)&=0 \\ H(n)&=n-H(H(H(n-1))), \quad n>0. \end{align}

The $Q$ sequence: \begin{align} Q(1)&=Q(2)=1, \\ Q(n)&=Q(n-Q(n-1))+Q(n-Q(n-2)), \quad n>2. \end{align}

Very little is known about these sequences. It is not even known, for instance, if the $Q$ sequence is always well defined, and never refers to $Q(0)$ or negative indices.

Compute the first few terms of these sequences.

These are possible Mathematica implementation: (the first few terms can also be computed by hand):

G[0] = 0;
G[n_] := G[n] = n - G[G[n - 1]]

H[0] = 0;
H[n_] := H[n] = n - H[H[H[n - 1]]]

These are the first 25 terms for the $G$ and $H$ sequences, respectively:

G: 1, 1, 2, 3, 3, 4, 4, 5, 6, 6, 7, 8, 8, 9, 9, 10, 11, 11, 12, 12, 13, 14, 14, 15, 16
H: 1, 1, 2, 3, 4, 4, 5, 5, 6, 7, 7, 8, 9, 10, 10, 11, 12, 13, 13, 14, 14, 15, 16, 17, 17

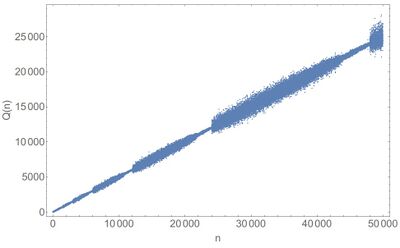
As can be seen, they appear to increase by unit step or stay constant, in an irregular manner. The $Q$ sequence is more interesting:

Q[1] = Q[2] = 1;
Q[n_] := Q[n] = Q[n - Q[n - 1]] + Q[n - Q[n - 2]]

These are the first few terms, which already show signs of less predictability, increasing with discontinuous steps (e.g., there is no 7), possibly also decreasing and with plateaux of varying sizes:

1, 1, 2, 3, 3, 4, 5, 5, 6, 6, 6, 8, 8, 8, 10, 9, 10, 11, 11, 12, 12, 12, 12, 16, 14

Plotting a larger number of them show some structure of breathing, alernating stabilization and sudden explosion in the magnitude of fluctuations.

The $10,000 sequence, or Conway sequence (also known as the Conway-Hofstadter sequence) is similarly defined as:

\begin{align}
  a(1) &= a(2) = 1, \\
  a(n) &= a\big(a(n - 1)\big) + a\big(n - a(n - 1)\big), \quad n > 2.
 \end{align}

It displays striking fractal properties. Explore this by plotting $a(n)-n/2$ for the first 16384 values (and relate it to the so-called Blancmange curve).

The Mathematica implementation:

a[1] = a[2] = 1;
a[n_] := a[n] = a[a[n - 1]] + a[n - a[n - 1]]
ListPlot[Table[a[n] - n/2, {n, 16384}], Frame -> True, 
 FrameLabel -> {"n", "a(n)-n/2"}, BaseStyle -> Large]

Produces the following plot:

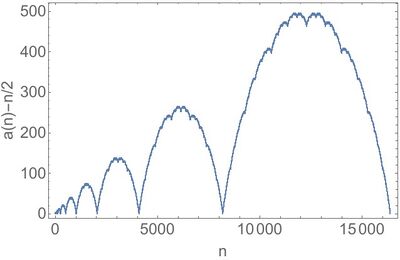
This shows a series of increasingly larger versions of the Blancmange function, which is a fractal (self-similar structure). The computation is trivial. The result is incredibly rich and complex. This is explored further with a more famous example that involves complex numbers. Note that the Conway $10,000 sequence (the name comes from a prize challenging to find some converging properties of the sequence) only involves integers, a so-called batrachion.

We now look at another beautiful illustration of computer power, that revealed an unsuspected complexity in simple-looking problems, which we have already commented on in our lecture on Complex Numbers. As put by Mandelbrot, take a number $c\in\mathbb{C}$ and form a sequence, a bit like the rabbits of Fibonacci, as follows:

$$z_{n+1}=z_n^2+c$$

with $z_0=0$. The question is, does the sequence $z_n$ diverge as $n\rightarrow\infty$? (meaning, if you remember your complex calculus, that its modulus $|z_n|$ eventually gets larger than any number you compare it to). By hand this is tedious. Let us check, as we did before, starting with $c=1$, in which case this will remain real throughout:

In[1]:= 1
Out[1]= 1

In[2]:= %^2 + 1
Out[2]= 2

In[3]:= %^2 + 1
Out[3]= 5

In[4]:= %^2 + 1
Out[4]= 26

and it's clear it'll diverge. Note that Mathematica uses % to refer to the previous result. Let's start with $i$ instead and use a dedicated command to iterate rather than doing it by hand:

NestList[(#^2 + I)&, 0, 10]
{0, I, -1 + I, -I, -1 + I, -I, -1 + I, -I, -1 + I, -I, -1 + I}

So this is oscillating, thus, remains bounded. If we track which points in the complex plane diverge (like 1) or converge (like $i$), we get a surprising result, that uncovers an entirely new type of geometry:

xmin = -2; ymin = -1; xmax = .5; ymax = 1; \[Delta]x = \[Delta]y = \
.0025;
Table[If[Abs[NestList[(#^2 + x + I*y) &, 0, 50][[-1]]]^2 < 10^7, 1, 
   0], {x, xmin, xmax, \[Delta]x}, {y, ymin, ymax, \[Delta]y}];
ArrayPlot[%]

One line of code, and an infinite landscape to explore. We'll leave it to you to travel the place (which you can do by changing xmin, xmax, ymin, ymax as well as the resolution.

Another problem, even simpler than Mandelbrot's complex (no pun intended) iterations, will make you famous if you solve it. It is called the Collatz conjecture. Conjecture means the result is supposed, and corroborated by various types of evidence, but not demonstrated. The problem is the following:

Take an integer $n$ and form a sequence as follows: if the current term is even, the next term is one half of the previous term (also an integer). If the previous term is odd, the next term is 3 times the previous term plus 1.

Easy, right, especially for a computer. Collatz's conjecture is that for all $n$, the sequence will always eventually reach 1.

Let us try, first by hand:

• 1→4→2→1
• 2→1
• 3→10→5→16→8→4→2→1

well, it's true so far. Is it always true? We can never know with a computer but we can test. This requires something that starts to look like computer coding, i.e., introducing possibilities depending on the current state of affairs. We can use the famous if loop for that, something like this:

If[EvenQ[n], n/2, 3 n + 1]

where EvenQ tests for the parity (true or false). Depending on which it is, one action, or the other, is taken. We can store the results in a list. The code would read like this:

n = 27; ln = {n};
While[n != 1, AppendTo[ln, n = If[EvenQ[n], n/2, 3 n + 1]]]

returning for this starting value, n=27:

{27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, \
242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, \
700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, \
668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, \
638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, \
7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, \
4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, \
122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, \
16, 8, 4, 2, 1}

It took some time, but here we are: ends in 1. Some quantity of interest in this case would be the length of the list in each case: does it grow as the number grows? Is there a pattern? Tough to say... Here's what the computer can tell us about this:

Table[ln = {n}; 
  While[n != 1, AppendTo[ln, n = If[EvenQ[n], n/2, 3 n + 1]]]; 
  Length[ln], {n, 1, 1000}];

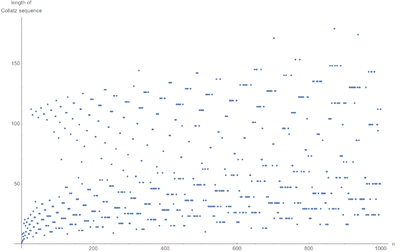
There is clearly a pattern emerging, but one that has escaped all Mathematical description so far. Erdös famously commented about it that "Mathematics may not be ready for such problems", which is a stunning statement given how simply this is stated! A computer can't solve the Collatz conjecture one way or the other, but it sure can implement it readily with a While and If.

Study this "optimization" (and formulation) of the Collatz conjecture. $$f(n) = \begin{cases} \frac{n}{2} &\text{if } n \equiv 0 \pmod{2},\\ \frac{3n+1}{2} & \text{if } n\equiv 1 \pmod{2}. \end{cases}$$

We conclude with the pinnacle of computer programming, Conway's game of life! This is a so-called cellular automaton, meaning that one simulates a space, or universe, of "cells" which state depends on given rules. Conway's universe is pretty simple: it is an infinite, square, chessboard-like space where each cell can take two states: 0 (dead) or 1 (alive). The rules to determine the state of a cell on the next iteration of the universe simulation depends on its current state along with the state of its eight immediate neighbours as follows:

1. Any live cell with two or three live neighbours survives.
2. Any dead cell with three live neighbours becomes a live cell.
3. All other live cells die in the next generation. Similarly, all other dead cells stay dead.

It's easy for a computer to implement, and simulate, such a universe. We can't describe an infinite universe but we could make it very large as a good approximation. Let us start very small instead:

nmax = 32;
map = Table[0, {i, 1, nmax}, {j, 1, nmax}];

The following shows the cell surrounding i0 and j0 (that we put here somewhere in the middle to stay off limit from the boundaries):

i0=15;j0=15;
map[[{i0 - 1, i0, i0 + 1}, {j0 - 1}]] = 1;
map[[{i0 - 1, i0 + 1}, {j0}]] = 1;
map[[{i0 - 1, i0, i0 + 1}, {j0 + 1}]] = 1;

That will serve as a good initial condition. We can display it with ArrayPlot[map]:

The code to run & iterate consists simply in joining the cells from the surrounding space, counting how many are there and apply the rules:

nextmap = map;
Do[
  naround = 
   Total[Flatten[{map[[{i - 1, i, i + 1}, {j - 1}]], 
      map[[{i - 1, i + 1}, {j}]], map[[{i - 1, i, i + 1}, {j + 1}]]}]];
  If[map[[i, j]] == 1 && (naround < 2 || naround > 3), 
   nextmap[[i, j]] = 0];
  If[map[[i, j]] == 0 && naround == 3, nextmap[[i, j]] = 1;],
  {i, 2, nmax - 1}, {j, 2, nmax - 1}];
map = nextmap;
ArrayPlot[map]

Note that we need to use two spaces: the original where we count, the second that we update. Would we do the updating on the fly, the surrounding cells would be counting in the future! Anyway, repeatedly running the previous code yields (read like a book, left-to-right and then down):

As you see, after some transient behaviour, one reach a cycle where the pattern repeats. This is called an oscillator in (Conway's game of) Life's terminology. This one has period 2 and is formed of three simpler period-2 oscillators, known as "blinkers". The four-blinker formation is called "traffic lights". One can find oscillators of any period, for instance, this pattern, discovered by Conway himself in 1970, named "pulsar", has period 3:

nmax = 32;
map = Table[0, {i, 1, nmax}, {j, 1, nmax}];

i0 = 10; j0 = 10;

map[[{i0 + 12}, Range[j0, j0 + 13]]] = 
  map[[{i0 + 7}, Range[j0, j0 + 13]]] = 
   map[[{i0 + 5}, Range[j0, j0 + 13]]] = 
    map[[{i0}, Range[j0, j0 + 13]]] = {{0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 
       1, 0, 0, 0}};

map[[{i0 + 10}, Range[j0, j0 + 13]]] = 
  map[[{i0 + 9}, Range[j0, j0 + 13]]] = 
   map[[{i0 + 8}, Range[j0, j0 + 13]]] = 
    map[[{i0 + 4}, Range[j0, j0 + 13]]] = 
     map[[{i0 + 3}, Range[j0, j0 + 13]]] = 
      map[[{i0 + 2}, Range[j0, j0 + 13]]] = {{1, 0, 0, 0, 0, 1, 0, 1, 
         0, 0, 0, 0, 1, 0}};

And this one, aptly named 1-2-3-4, is a period 4 oscillator:

nmax = 32;
map = Table[0, {i, 1, nmax}, {j, 1, nmax}];
i0 = 12; j0 = 12;

map[[{i0 + 10}, Range[j0, j0 + 10]]] = 
  map[[{i0 + 8}, Range[j0, j0 + 10]]] = 
   map[[{i0}, Range[j0, j0 + 10]]] = {{0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0}};
map[[{i0 + 9}, Range[j0, j0 + 10]]] = 
  map[[{i0 + 1}, Range[j0, j0 + 10]]] = {{0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0}};
map[[{i0 + 2}, Range[j0, j0 + 10]]] = {{0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0}};
map[[{i0 + 3}, Range[j0, j0 + 10]]] = {{0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0}};
map[[{i0 + 4}, Range[j0, j0 + 10]]] = {{1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1}};
map[[{i0 + 5}, Range[j0, j0 + 10]]] = {{1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1}};
map[[{i0 + 6}, Range[j0, j0 + 10]]] = {{0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0}};

There are much more interesting patterns in this simple cellular-automaton. Simple by the rules that define it, that is. Actually, all the possible patterns are in there, somewhere. We will come back to it several times, but for the time being, it should be clear how one can seek the computer's assistance to track the fate of such simple computer problems. Both Mandelbrot and Conway were studying these things by hand, initially. This is something from the past, although you may have fun checking some configurations for yourself!