Crash Course in Scientific Computing
VI. Random Numbers
We now turn to another types of special numbers, which also have a special type of relationship with computers, namely, random numbers. That will allow us to play with things that computers are good at (e.g., with statistics). We'll need another package first:
import Pkg; Pkg.add("Distributions")
Once this is done (once for ever on a given machine), you can then be:
using Distributions
What is a random number? Something you can't predict, e.g.,
julia> rand() 0.663764152328755 julia> rand() 0.017345425057746944 julia> rand() 0.6186819567638984
although in these three cases, one can see that the numbers are between 0 and 1, so it is tempting to predict they'll maintain that pattern, and one can check they do. This is because even random numbers follow some rules, or law, or, more accurately, distribution. Namely, the distribution of random numbers is the mathematical functions that gives the probability that any given sampling will be found in a given range. The rand() distribution returns a random number uniformly (i.e., with same probability) distributed between, indeed, 0 and 1. To see that with our own eyes, let us generate ten thousands such random points and plot an histogram, which is a sort of empirical distribution, approaching the theoretical one that generates the numbers from a sampling of its output:
lst=[rand() for i=1:10^5]
and after
using Plots
histogram(lst)
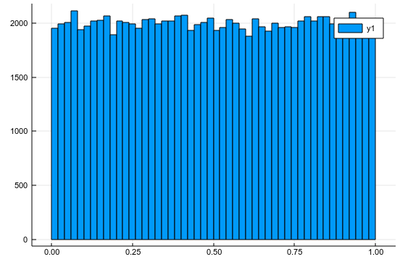
As expected. The fact that this is not a straight line but jumps from one window to the other is called "fluctuation". This is typical of random numbers. The more we have, the less they will fluctuate around their theoretical value. Now let us ask ourselves, what would be the distribution if we square each random number after drawing it? We can call $X$ the so-called random variable which returns a random number following a given distribution, here, uniform between 0 & 1, so we could write $X\to U([0,1])$. We are then asking, what is the distribution of $X^2$? Is it still uniform? One thing is for sure, is that since $0\le X\le 1$, then also $0\le X^2\le1$. Let us ask the computer what it finds:
lst=[rand()^2 for i=1:10^5]
histogram(lst)
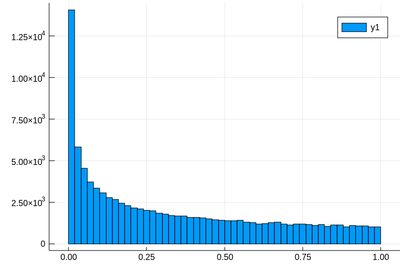
This has a clear structure which is not the straight line anymore. Not surprisingly, squared numbers are not uniform. Some people explain it as the square of a small number being smaller than the number itself, so will tend to pile up towards zero. But then if we turn to, say, the random variable $2X$, which uniformly distributed over $[0,2]$, shouldn't we expect numbers above 1 to clutter towards larger values? But $(2X)^2$ is $4X^2$ and multiplying by 4 the $X^2$ random variable, which has the shape shown above, will not change its structure. More accurately, therefore, this is due to the concavity of the function, rather than its relation to the identity. We can get a better understanding by hunting the theoretical result, which the computer can help us to check, or give us clues, but we shouldn't rely on the computer alone to understand what is going on.
The exact result is obtained by differentiating the cumulative function, $f_{X^2}=dF_{X^2}/dx$, with $F_{X^2}(x)\equiv\int_0^x f_{X^2}(y)\,dy$. This follows from the fundamental theorem of calculus. Now, since from the interpretation of $f_{X^2}$ as a density of probability, we have
$$F_{X^2}(x)=\mathbb{P}(X^2\le x)$$
where $\mathbb{P}(X^2\le x)$ is the probability for $X^2$ to be less than $x$, then we can compute $\mathbb{P}(X^2\le x)=\mathbb{P}(X\le\sqrt{x})=\sqrt{x}$, since the probability is uniform. Therefore:
$$f_{X^2}(x)={1\over2\sqrt{x}}\,.$$
Let us check:
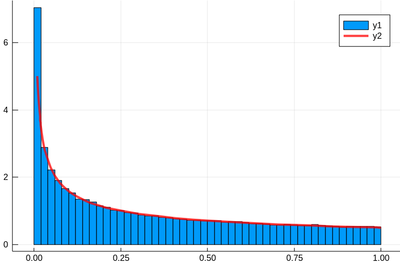
f(x)=1/(2*sqrt(x))
histogram(lst,norm=true)
plot!(f,.01,1, linewidth = 4, linecolor = :red, linealpha=0.75)
Remember that ! means to plot on the existing display and we've used the option norm=true to normalize the histogram, effectively turning it into a probability distribution. This seems to work indeed:
Let's have a look at the distribution of inverse random numbers, also sampled from a uniform distribution between 0 and 1. This time, the support is infinite (it is $[1,\infty[$). The theoretical distribution is $f_{1/X}=d\mathbb{P}_{1/X}/dx$ with $\mathbb{P}_{1/X}=\mathbb{P}(1/X\le x)=\mathbb{P}(X\ge 1/x)=1-1/x$ (being uniform again), so that $f_{1/X}(x)=1/x^2$.
This time we'll use a lot of points to make sure we get the exact result:
@time lst = [1/rand() for i=1:10^8]
The @time allows us to benchmark the time and memory resources involved. As you can see, on a 2020 machine, it's pretty fast (for a hundred million points!)
0.427357 seconds (67.69 k allocations: 766.257 MiB, 0.65% gc time)
The result is also consequently very smooth:
@time histogram(lst,norm=true,bins=0:.01:10)
returning
4.644046 seconds (4.88 k allocations: 1.490 GiB, 1.74% gc time)
and, after also
f(x)=1/x^2
plot!(f,1,10,linewidth=4,linecolor=:red,linealpha=.75)
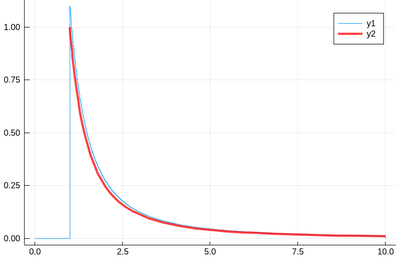
This is slightly off, clearly. The culprit is our empirical (i.e., computed) distribution function, which density should be 1 at $x=1$ and is more than that. The problem is the norm option of histogram, which normalizes to what is plotted (or retained). And we have points beyond that. It would work better if we'd plot more points but we wouldn't see much over a larger range. Instead, we can use the correct number to renormalize our theory plot. This is how many numbers we have:
sum(lst .< 10)
We leave its proper normalization as an exercise.
Normalize the histogram of $1/X$ so as to fit the theoretical value.
Instead of normalizing the histogram itself, it is equivalent, and simpler, to normalize the theoretical distribution itself.
julia> lst=[1/rand() for i=1:10^8] julia> histogram(lst,norm=true,bins=0:.01:10, label="computer") julia> plot!(x->1e8/(sum(lst.<10)*x^2), 1, 10, lw=3, lc=:red, la=.75, label="theory")
This indeed shows the good agreement between computer-generated distribution and theory when normalizing properly:
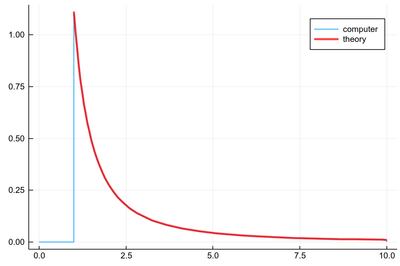
In this case, we normalized the theory to correct for the shortcoming of the histogram which does not seem to take an option to be normalized to something else than 1! We leave it as a further exercise to do this anyway.
Although this is not needed, this is the list of the numbers we excluded:
lst[lst .> 100]
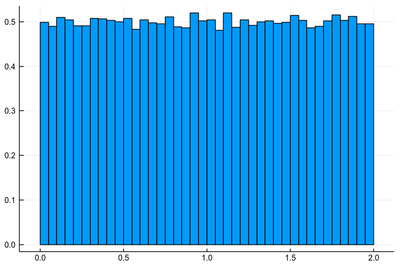
Let us look at other operations on random variable. You can easily convince yourself that rescaling a random variable $X$ by a constant $\alpha$ merely rescale the range of these numbers, or the support of the distribution, which needs to remain normalized though so in effect we are stretching the space. For instance $2X$ has its distribution function normalized to $1/2$:
histogram([2rand() for i=1:10^5], norm=true, legend=false)
How about, not $2X$, which is of course $X+X$, but $X+Y$ where both $X$ and $Y$ follow the same uniform distribution $U([0,1])$. Is that $2X$ again since $X$ and $Y$ are the same? Careful: the fact that $X$ and $Y$ follow the same distribution does not mean that they are equal, $X\neq Y$. Each time that we look at the variable, it takes a different value (it is random)
julia> X, Y = rand(), rand()
(0.023904897028309557, 0.8702240210821197)
julia> X==Y
false
The actual instances are different but surely the distribution would be the same and that of $2X$ (or $2Y$)? Let us find out:
histogram([rand()+rand() for i=1:10^5], norm=true, legend=false)
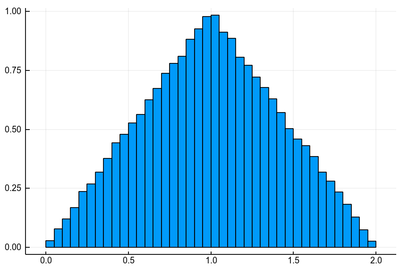
Clearly not uniform. In fact, it is an exact triangle! The phenomenon here is that while $X$ and $Y$ can take any value between 0 and 1 with the same probability, it is more likely for their sum to be close to their average. If that surprises you, do the same reasoning with two dices. What probability do you get to draw a 7 as compared to drawing a 2 or a 12? The exact distribution for $X+Y$ can be found by similar reasoning but with a continuous variable. It is easily done geometrically. More generally, in probability theory, one can show that the sum of two independent random variables follows the distribution given by the convolution of the distribution of the random variables, which also explains this triangular shape and allows to extend it to greater sums
$$\sum_{i=0}^n X_i\label{eq:sumX}$$
which give rise to the Irwin-Hall distributions:
Consider the sum of $k$ independent random variables $X_i$ uniformly distributed over $[0,1]$. Study numerically the distribution function of their sum, Eq. \eqref{eq:sumX} and check that this is given by the Irwin-Hall formula:
$${f_{X}(x;n)={\frac {1}{2(n-1)!}}\sum _{k=0}^{n}(-1)^{k}{n \choose k}(x-k)^{n-1}\operatorname{sgn}(x-k)}\label{eq:irwinhall}$$
where
$${\operatorname {sgn}(x-k)\equiv{\begin{cases}-1&x<k\\0&x=k\\1&x>k.\end{cases}}}$$
We can first define the necessary functions:
function sgn(x,k)
if x<k
-1
elseif x>k
1
else
0
end
end
function IrwinHall(n, x)
(1/(2*factorial(n-1)))*total(
[(-1)^k*(x-k)^(n-1)*sgn(x,k)*binomia(n,k)l for k∈0:n]
)
end
and then go directly to business:
histogram([rand()+rand()+rand() for i=1:10^5], norm=true, label="X1+X2+X3")
plot!(x->IrwinHall(3,x), -1,4, lw=4, lc=:red, la=.75, label="Irwin Hall")
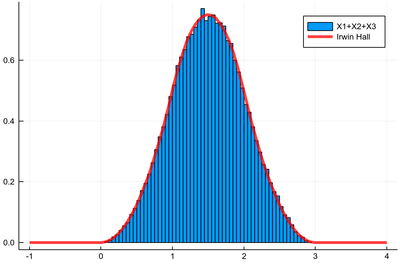
From this, it is easy to generalize, e.g., the sum of seven random variables along with all distributions up to 10 can be shown together with:
histogram(sum([[rand() for i=1:10^5] for j=1:7]),norm=true,label="X1+...+X7")
for k∈1:10
global p=plot!(x->IrwinHall(k,x), -1:.01:7, lw=2, la=.75, label="x", label="Irwin Hall $(k)")
end
p
The result is shown in the main text below.
Equation \eqref{eq:irwinhall} is a funny composition of functions, namely, stiched piecewise polynomials (so-called splines). for instance, the case $n=3$ gives:
$${f_{X}(x)={\begin{cases}{\frac {1}{2}}x^{2}&0\leq x\leq 1\\{\frac {1}{2}}(-2x^{2}+6x-3)&1\leq x\leq 2\\{\frac {1}{2}}(x-3)^{2}&2\leq x\leq 3\end{cases}}}$$
which, regardless of its odd definition, has a very natural look especially as $n$ becomes larger. From the above exercise:
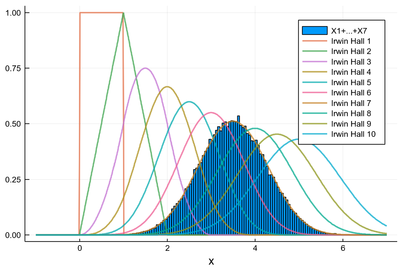
In the limit where $n\to\infty$, these distributions tend to some familiar function: the Gaussian. This is the result of the so-called central limit theorem that asserts that, not only uniform distributions, but any type of independent random variables, when summed in large numbers, tend to what is called a normal distribution, where the denomination of "normal" comes from its widespread occurrences and natural-looking character, making it the distribution one expects to find when things are "normal".
The normal distribution takes two parameters, the mean $\mu$ and the standard deviation $\sigma$. This is how we define such a distribution in julia (here with mean 1 and standard deviation 0.5):
julia> dist=Normal(1.0, .5)
Normal{Float64}(μ=1.0, σ=0.5)
We can now generate normally-distributed random numbers:
julia> rand(dist) 0.6696409682501712 julia> rand(dist) 0.6985762003105883 julia> rand(dist) 1.8506284482154651
In the laboratory, we would ask you to find the mean of a normally distributed random variable by using five points. Does it work?
julia> mean([rand(dist) for i=1:5]) 0.6439917898168767
Ouch! We were expecting 1!
julia> dist.μ 1.0
So? Oh! We're doing statistics... things vary from one realization to the other:
julia> mean([rand(dist) for i=1:5]) 0.5196060896076187 julia> mean([rand(dist) for i=1:5]) 1.109368345414772 julia> mean([rand(dist) for i=1:5]) 1.1134351116298737 julia> mean([rand(dist) for i=1:5]) 1.235455527271116 julia> mean([rand(dist) for i=1:5]) 1.2718188614651438
Of course, there are a lot of fluctuations... We had, after all a big standard deviation:
julia> dist.σ 0.5
So don't forget to plot error bars in your graphs!
An important theme of statistics is to study the statistical behaviour of statistical quantities, e.g., how does the mean itself fluctuate? Let's find out:
sample=[rand(dist) for i=1:10^5];
histogram(sample, norm=true, label="Normally distributed numbers")
samplemean=[mean([rand(dist) for i=1:5]) for j=1:10^5];
histogram!(samplemean, norm=true, label="Distribution of their mean")
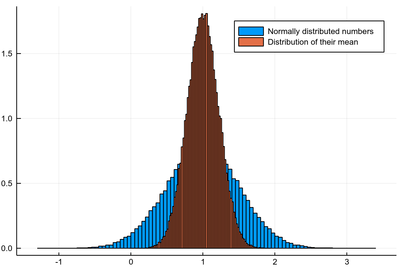
The different bin-sizes is due to the different support for both cases, this could be enforced with the bins option.
So the mean looks like it's also fluctuating normally, with the same mean but with a different (smaller) standard deviation. In fact, one can show that the standard deviation $\sigma_M$ of the mean of $N$ numbers relates to the standard deviation $\sigma$ of the numbers themselves (if normally distributed) as follows:
$$\sigma_M={\sigma\over\sqrt{N}}$$
What is the distribution of the standard deviation $\sigma=\sqrt{\operatorname{var}(X)}$? This cannot be normal since it must be a positive number, the square root of the variance $\operatorname{var}$ which is itself, for $n$ numbers, defined as:
$$\operatorname{var}(\{x_1,\cdots,x_n\})={1\over n}\sum_{i=1}^n(x_i-\overline{x})^2\label{eq:var}$$
where $\overline{x}$ is the sample mean.
What to expect then? Let's ask the computer before we ask the theory:
histogram([std([rand(dist) for i=1:3], corrected=false) for j=1:10^5],
norm=true, label="Distribution of standard deviation")
The option corrected=false is to ensure that std computes the square root of the variance as defined by Eq. \eqref{eq:var}, since there are various definitions.
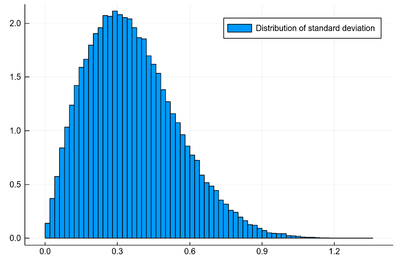
Clearly the standard deviation is not normally distributed. Remember that the standard deviation of the initial distribution was $\sigma=1/2$. Can we get access to that?
julia> mean([std([rand(dist) for i=1:3], corrected=false) for j=1:10^5])
0.36240524388003825
julia> mean([std([rand(dist) for i=1:3], corrected=false) for j=1:10^5])
0.36003512501085244
julia> mean([std([rand(dist) for i=1:3], corrected=false) for j=1:10^5])
0.36149996456935973
Not really, or at least not immediately... We have here the phenomenon of a biased estimator, whereby the mean of something which we use to estimate, from a sample, the actual value of the whole set, does not converge to the good value, but somehow overestimate or underestimate it. Theory tells us that the distribution of the standard deviation is a complex function involving the $\Gamma$ function, whose mean is related to the standard deviation of the starting distribution by a factor of $\sqrt{2/N}\Gamma(N/2)/\Gamma((N-1)/2)$ where $N$ is the number of points used to estimate the standard deviation. And indeed:
julia> using SpecialFunctions
julia> c4=sqrt(2/N)*gamma(N/2)/gamma((N-1)/2)
0.7236012545582677
julia> mean([std([rand(dist) for i=1:3], corrected=false) for j=1:10^5])/c4
0.5011040338393551
which is the good result ($\sigma=1/2$). So there is a way to do an unbiased estimation of standard deviation (if we know the distribution is normal). In fact, such bias from the estimators is the reason why the variance is usually not taken as Eq. \ref{eq:var} (with the corrected=false option in std) but as:
$$s^{2}={\frac {1}{n-1}}\sum_{i=1}^{n}\left(x_{i}-{\overline {x}}\right)^{2}$$
The $1/(n-1)$ is known as Bessel's correction. It makes the variance an unbiased estimator. The standard deviation, even with Bessel's correction, is still biased because the square root is nonlinear and does not commute with the mean.
While standard deviation can be quite tricky, the mean is much better behaved in general: the sample mean is an unbiased operator of the true mean, regardless of the distribution... provided, however, nothing naughty happens. Let us now explore numerically a very interesting (and important) phenomenon, showing that even the mean can badly behave.
For that, we will need the Cauchy function from the above-loaded "Distributions" package. This is a histogram of $10^5$ Cauchy-distributed points:
histogram(rand(Cauchy(),10^5))
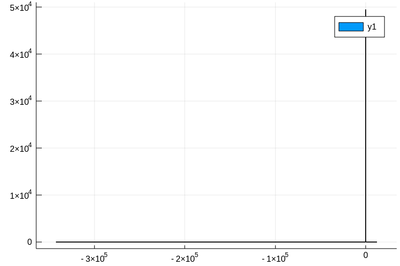
And indeed this looks badly behaved already! For such a wild distribution, the binning option is mandatory:
histogram(rand(Cauchy(),10^5),bins=-10:.5:10,norm=true)
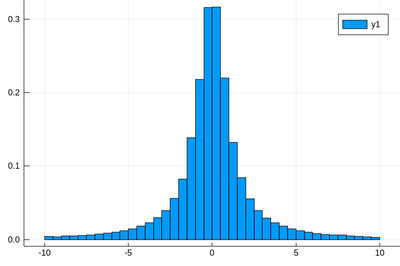
This is a nice histogram, what's wrong with this distribution? Let us compute its mean, which seems clearly to be zero. The mean-sample should be a good (unbiased) estimator of the true mean. Let's take a lot of points so that we'll get an accurate value:
julia> mean(rand(Cauchy(), 10^5))
-4.311191733016311
julia> mean(rand(Cauchy(), 10^5))
-0.06472103358790318
julia> mean(rand(Cauchy(), 10^5))
48.96157141643905
We first get fairly expected results, as the "standard deviation" sounds around 2 or so, but this 48.96 seems wrong... With 10000 points we don't expect large mistakes or uncanny fluctuations. Let's plot the mean to embrace lots of realization in one plot:
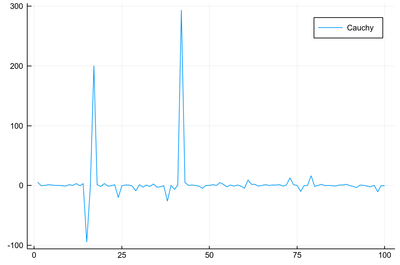
Indeed we get, most of the time, reasonable results, but time to time, huge departures. Maybe we didn't take enough points after all. Let's try with the mean of 10 million points! That's excessively huge. If that doesn't solve the problem, nothing will:
julia> @time lm=[mean(rand(Cauchy(), 10^7)) for i∈1:100];
30.946617 seconds (101.60 k allocations: 7.456 GiB, 1.81% gc time)
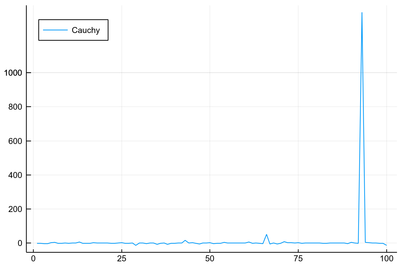
My, it is even worst! If we go so far as to average over ten million points, we can still find "estimates" of
julia> maximum(lm)
1354.1721326414633
This behaviour of the Cauchy distribution is very different from that of the normal distribution. Namely, it fluctuates to all orders, in the sense that a random variable that follows such a law can take arbitrarily large values. This means that once in a while, a point will lie very far from the cloud of the others. Such points are known as outliers. On the contrary, "normal" fluctuations are contained within their interval of standard deviation. Outliers there, although still possible, are so improbable that they are considered errors.
The distribution function of the Cauchy distribution is a Lorentzian. It is a basic lineshape of fundamental physics (the Fourier transform of the exponential, which corresponds to memoryless decay so this is the lineshape of particles). What distinguishes it from the Gaussian distribution, which also has infinite support so could also in principle return any value whatsoever, is the so-called "fat tails" that shows how, for enough repetition of our luck, we eventually fluctuate far enough:
julia> julia> lst=rand(Cauchy(),10^8);
julia> histogram(lst,bins=-10^7:10^4:10^7,norm=true,
yscale=:log10,label="Cauchy histogram")
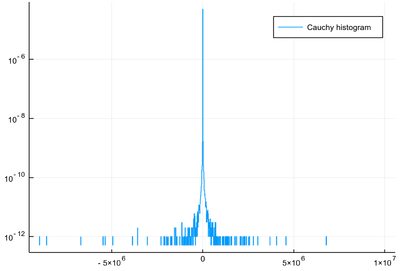
The following shows the intrinsic difference between Cauchy and Normal:
julia> lmNormal=[mean(rand(Normal(), 5)) for i∈1:100];
julia> lmCauchy=[mean(rand(Cauchy(), 5)) for i∈1:100];
julia> plot([lmCauchy, lmNormal], label=["Normal" "Cauchy"],
ylims=(-25,25),legend=:bottomright)
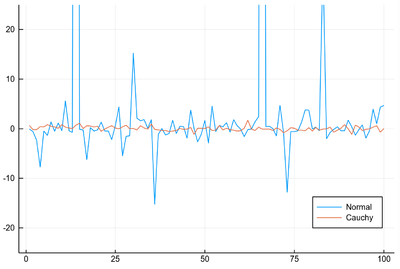
This is an example of a distribution that cannot be characterized by a standard deviation. It cannot even be characterized by its mean, it does not have any! By sampling from this distribution, eventually, an outlier will by itself overrule all the other points of the set, thus spoiling the concept of average. The mean itself will not be normally distributed! Note that in the above plot, we have limited to small values of $y$ as otherwise the huge fluctuations of the Cauchy distribution would make the Normal one looks exactly constant.
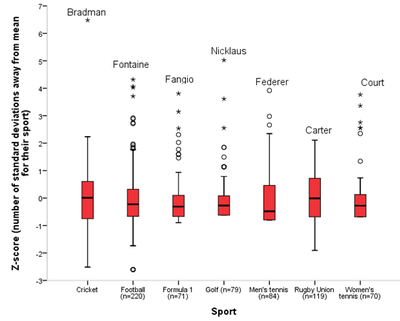
This failure of the mean is common in complex systems. For instance, in a human's society, it is typically useless (or deceptive) to consider the mean when speaking of, e.g., wealth. A rich man is somebody's else poor. The average person's wealth in a city is typically that of the richest person. The following graph shows how a similar concept now in sport, with the most important departure ever noted being in cricket (from [1]):
The study of the statistical properties of such quantities derived from samples of a larger population ruled by an hypothetical rule is the topic of an entire field of its own: inferential statistics. This is fit either for a course on its own, or for your personal investigation, so we will leave this topic for now, although it is very important for Physics, where one deals with experimental data (and for society at large, where one deals with polls and statistics of virus contamination).
Above, we have dealt with continuous distributions, but there are also discrete distributions, for which the random variable takes discrete values (a finite or infinite number of them depending on the distribution).
The most important one is the Poisson distribution. It takes one parameter
julia> P=Poisson(3)
Poisson{Float64}(λ=3.0)
It gives the number of events that can happen in the unit time:
julia> rand(P)
5
julia> rand(P)
1
julia> rand(P)
1
julia> rand(P)
1
julia> rand(P)
2
julia> rand(P)
3
julia> rand(P)
0
The probability to get any particular number is given by the Poisson distribution:
$$P(k)={\lambda^k\exp(-\lambda)\over k!}$$
julia> λ=3
julia> histogram([rand(P) for i=1:10^5],norm=true,bins=0:15)
julia> plot!(collect(0:15).+.5, [λ^k*exp(-λ)/factorial(k) for k=0:15], lw=4, lc=:red)
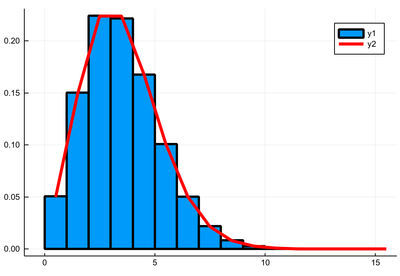
Discrete probability distributions are easier to work with as they give directly probabilities. The normalization condition reads $\sum_k P(k)=1$ where the sum is taken over all the values that the random variable can take, in this case, $0\le k<\infty$. You can check the normalization exactly or numerically:
julia> sum([λ^k*exp(-λ)/factorial(k) for k=0:15])
0.9999998759198293
For such a distribution, the variance is equal to the mean. There are many different (but ultimately, equivalent) ways to check that:
julia> lP=rand(P, 10^5);
julia> var(lP)
3.0076510204102047
julia> std(lP)^2
3.007651020410205
julia> mean(lP.^2)-mean(lP)^2
3.0076209438999992
julia> mean((lP.-mean(lP)).^2)
3.0076209439000006
We let you explore these and other features on this and other distributions, including those you make up yourself. Any normalized, positive function indeed serves as a possible probability distribution, but how to draw random numbers from them? In fact, how does the computer generate non-uniform random numbers in the first place? Where does it get its uniformly distributed ones?
One should speak, as far as computers are concerned, of pseudo-random numbers, i.e., numbers that appear to be random but actually are produced by a deterministic process known as a PRNG (Pseudo-Random-Number-Generator). The most popular such generator is the linear congruential generator algorithm that defines pseudo-random number $X_n$ according to the sequence:
$$X_{n+1}=\left(aX_{n}+c\right){\mod {m}}$$
where $m>0$ is the modulus, typically a prime or a power of 2, $a$ such that $0<a<m$ is the multiplier and $c$ such that $0\le c<m$ is the increment.
Implement a Pseudo-Random Number Generator from the linear congruential formula with $m=2^{32}$, $a=1664525$ and $c=1013904223$. Observe how the knowledge of your seed (initial value $X_0$) determines completely the whole sequence, however random it might appear to be. The parameters offered are part of a standard sample for this method (numerical recipes). What is the probability that from a billion randomly sampled points you might be able to recognize the PRNG at work?
Once you have uniformly distributed random numbers, you can turn to a pseudo-random number sampling method, which distributes them differently. A simple method that works for any distribution in any dimension is rejection sampling. It consists in distributing randomly a point on the domain of the distribution (?!) and retain it, through another random sampling between 0 and the maximum value of the distribution, it is bounded by the value of the distribution at its present location. The fact that the comparison is to the maximum value of the distribution means that we are comparing two probabilities, one from the computer (rand()), the other from the distribution times some constant which serves as the volume element, unnormalised, but we do not care about normalization which could be implemented a-posteriori without changing the results, so with no need of implementing it at all, which is a welcome simplification. A drawback of this method is that it is not very efficient as many points can be lost, depending on the volume covered by the distribution itself in its tightest enclosing space, so peaked distributions are particularly ineffective. But it is simple and general enough to keep in one's bag of survival tools.
Produce a random number that distributes points randomly in a circle. Study the distribution of $r$ and $\theta$ for these points and conclude as to the suitability of the "naive" approach that randomly samples the radius and angle. Note that in this case, the ratio of valid vs rejected points has a particularly important meaning and in some approach to this problem even constitutes the quantity of interest.
Produce a random number generator in 1D and 2D on some distribution of your choice and animate the process to clarify the mechanism to a wide audience.
Links
- Related discussion from my Computación I lectures at the Universidad Autónoma de Madrid.