Crash Course in Scientific Computing
XVII. Ordinary Differential Equations: Euler & Heuhn
Let us now turn to one of the most wanted tasks of scientific computing: solving differential equations. What a differential equation is in the first place is part of our Mathematics lectures and we refer you to that to get a refresher, but in a nutshell and to fix ideas, we refer to equations of the type:
$$\label{eq:ODE1} y'(t)=f(t,y(t))$$
where $y$ is the unknown—what we like to call $x$ in "normal" equations—except that here $y$ is a function, not a variable that can take a single value. If it is a function of the variable $t$, one must specify the value of $y$ at all $t$ to solve this so-called Ordinary Differential Equation (ODE), as the classification goes when there is only one variable (several variables coming next). It is also first-order since we presently limit ourselves to the first derivative. Here $f$ is another function of both the variable, or parameter, $t$ and of the "unknown" object of interest $y$. What is a function of a function? Technically this is called a "functional" and can become quite a murky business but in our case, this is just to say that we allow any tweaking and operations on the function itself, and that the derivative at each point must correspond to such an operation on the function. For instance, here is a celebrated ODE:
$$\label{eq:basicODE}y'(t)=-y(t)$$
In this case $f(t,y)=-y$ (it is not "using" the variable "slot"). This says that the derivative is proportional to the magnitude of the function: the larger is the function, the steeper its slope should be. The smaller it is, the more horizontal it should be. One can already see how the $y=0$ will be an asymptote for such a function. In fact, you should by now already see that such a differential equation has an easy solution, namely, $y(t)=y(0)\exp(-t)$. The point of numerical methods is that it will allow you to solve equations that have no such easy, or even possible, closed-form expression, such as:
$$y'(t)=\sqrt{y(t)^2+t^2}$$
In this case, one can try to reconstruct a function $y$ such that its derivative, or slope, at all times $t$, is equal to the distance of the function from the origin. Here too one can get some intuition on the solution, for instance as time passes, the slope increases so this, in contrast to the previous case, should have an explosive nature with a vertical as an asymptote. The computer will later tell us if our intuition is correct.
The most famous and straightforward algorithm is known as Euler's method (we'll start there) and the most popular is the so-called RK4 variant of the Runge–Kutta methods. In between are a large variety of possible implementations, many related in some way or the other. If you understand the main methods, you'll be fine in adapting others if they should be needed.
Methods can further be classified as "explicit"—when the solution only depends on quantities already known—or "implicit", when the solution involves other unknowns which require solving additional equations. Euler's method is explicit and, as the simplest method, is also the typical starting point to introduce the basic idea of solving ODE. Not surprisingly, it is also one of the least efficient so we will have to look at other methods, and it also suffers from problems such as instabilities, producing spurious oscillations, so we may have to consider equally inefficient but more stable methods, such as the "Backward Euler method" which, in turn, is implicit so it'll allow us to understand how one can solve equations relying on unknown quantities!
But first with the easy Euler method: we discretize time (we'll all our variable like this to fix ideas) into steps $t_1$, $t_2$, $\cdots$, $t_n$ separated by the same interval $h$. The sought solutions at these times are denoted $y_n\equiv y(t_n)$. Back to \eqref{eq:ODE1}, approximating $y'(t)\approx (y(t+h)-y(t))/h$, we have:
$$y_{n+1}=y_n+hf(t_n,y_n)$$
This is very simple since from the solution $y_n$ at time $t_n$ we can compute the solution at $t_{n+1}$. Explicitly. Hence the name.
Let us solve, for instance, Eq. \eqref{eq:basicODE} numerically, which is good not to solve the equation but to study the method itself by comparing it to the known solution:
npts = 100; # number of points
y=0.0*collect(1:npts); # predefine the array
h=.1; # timesteps, so total time = npts*h=10
# The differential equation to solve
function f(t,y)
-y
end
y[1]=1; # initial condition
# The numerical method (Euler's)
for i=1:npts-1
y[i+1]=y[i]+h*f((i-1)*h,y[i])
end
And we can now compare the numerical solution to the real one:
plot(((1:npts).-1)*h, [y[i] for i=1:npts], label="Euler", xlabel="t", ylabel="y'=-y")
plot!(x->exp(-x),0, 10, label="Exact")
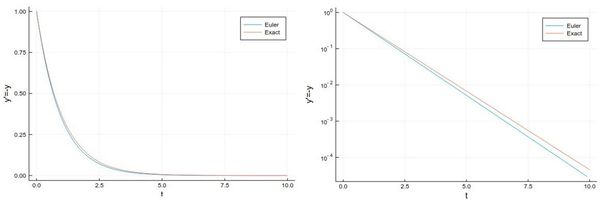
So we can see how it works but approximately only. While Eq. \eqref{eq:basicODE} is a venerable, universal case, we will turn to another, more particular case which also features oscillations, so that we can get a better look at the failures of the solution. Namely, we will use the following equation
$$y'={y\over 2}+2\sin(3t)\label{eq:PaulODE}$$
whose solution can be found with an integrating factor [1]
$$y=-{24\over37}\cos(3t)-{4\over37}\sin(3t)+\left(y(0)+{24\over 37}\right)e^{t/2}$$
We will get rid of the transient part by setting $y(0)=-24/37$ so as to focus on the oscillatory character. Bad failures of our method will be apparent from a drift of the oscillations. Other failures such as incorrect amplitude of frequencies are probably less serious. In the above case, the differential equation is defined as:
function f(t,y)
(y/2)+2sin(3t)
end
And the method can be quickly implemented as:
tmax=4*pi;
h=0.0001;
npts=round(Int64,tmax/h);
y=0.0*collect(1:npts);
y[1]=-24/37
for i=1:npts-1
ti=(i-1)*h
y[i+1]=y[i]+h*f(ti,y[i])
end
with various repetitions of
plot!(((1:npts).-1).*h, y,
xlabel="t", ylabel="y", label="h=$(h)",
legend=:bottomleft,ylims=(-2,.75),lw=3)
to see the effect of different time steps:
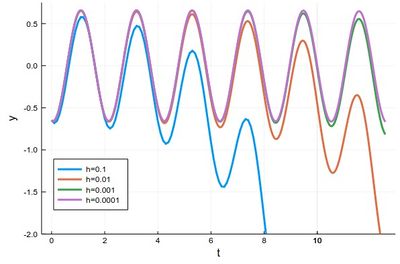
Comparing to the exact solution shows that the error gets quickly sizable, even with a lot of points:
plot(abs.([-(24/37)*cos(3t)-(4/37)*sin(3t) for t in ((1:npts).-1).*h]-y),
lw=3, color=:red, xlabel="index array", ylabel="error", legend=false)
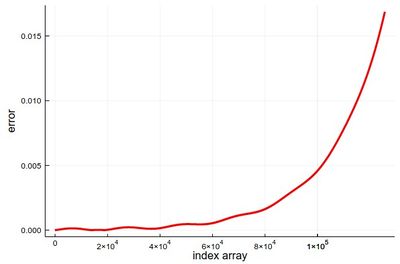
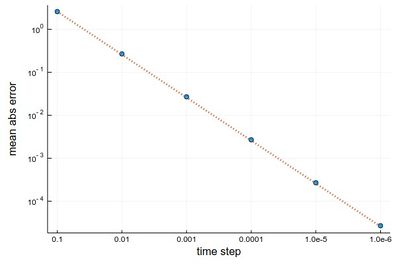
We can analyze the error in more details:
hlist=[10.0^(-k) for k=1:6];
herror=[];
for h in hlist
npts=round(Int64,tmax/h);
y=0.0*collect(1:npts);
y[1]=-24/37;
@time for i=1:npts-1
ti=(i-1)*h
y[i+1]=y[i]+h*f(ti,y[i])
end
append!(herror,mean(abs.([-(24/37)*cos(3t)-(4/37)*sin(3t) for t in ((1:npts).-1).*h]-y)))
end
produces on wulfrun2:
0.000689 seconds (880 allocations: 15.813 KiB) 0.003283 seconds (11.78 k allocations: 203.766 KiB) 0.025673 seconds (136.18 k allocations: 2.270 MiB) 0.314037 seconds (1.38 M allocations: 22.979 MiB, 1.45% gc time) 2.519780 seconds (13.82 M allocations: 230.066 MiB, 1.00% gc time) 26.261842 seconds (138.23 M allocations: 2.247 GiB, 2.43% gc time)
and a nice linear decay of the error with the timestep (so no-round off error, because essentially it becomes impractical to take a smaller timestep):
That's basically it for the explicit Euler method. Let us now have a look at its fancier cousin, the so-called Backward Euler method, which is implicit. It consists in taking the slope from the right point rather than the left:
$$y_{n+1}=y_{n}+hf(t_{n+1}, y_{n+1})$$
With infinitesimals, both definitions converge to the same value, but in a discretized space, it brings the explicit method Eq. \eqref{eq:basicODE} to the implicit method where the unknown value $y_{n+1}$ appears on both sides of the equation. This, therefore, brings a new equation of its own, that we need to solve on its own. In this case, a fixed point method, i.e., iterating
$$y_{n+1}^{[i+1]}=y_{n}+hf(t_{n+1}, y_{n+1}^{[i]})$$
until $|y_{n+1}^{[i+1]}-y_{n+1}^{[i]}|<\epsilon$, is usually working well. This is a possible julia implementation:
itmax=100; # at most 100 iterations for the fixed-point
h=0.1;
tmax=4*pi;
npts=round(Int64,tmax/h);
y=0.0*collect(1:npts)
y[1]=-24/37;
for i=1:npts-1
it=0; # to count iterations
ykp=y[i];
yk=ykp+1;
while abs(ykp-yk)>0 && it<itmax
it+=1;
yk=ykp;
ykp=y[i]+h*f(h*(i+1),yk)
end
# println("On iteration $(it), error is $(abs(ykp-yk))")
y[i+1]=ykp
end
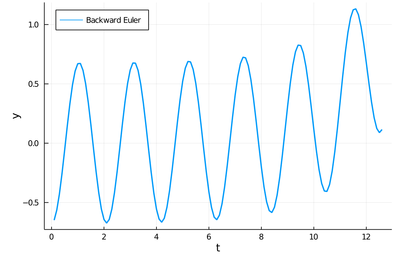
plot(([1:npts]*h, y), lw=2, xlabel="t", ylabel="y", label="Backward Euler", legend=:topleft)
With h=0.1, this gives a similar result for Paul's ODE with the drift now in the other direction. It is more stable (which we don't see here as Euler was also stable in this case) but it is not much better, if at all, than the explicit method, while it was definitely more complex to implement.
Euler's methods work but none is very accurate. It can be improved by considering a better estimation for the tangent. The idea is to use not the tangent of $y$ at $t_n$ only but also at $t_{n+1}$ and take the average:
$$\begin{align} y_{n+1}&=y_n+{1\over2}(y'(t_n)+y'(t_{n+1}))\\ &=y_n+{h\over 2}[f(t_n,y_n)+f(t_{n+1},y_{n+1})]\end{align}$$
Of course, we do not know $y_{n+1}$, so the method would appear to become implicit and require another separate solution as for the Backward Euler. But we can also simply use Euler's explicit method to estimate it:
$$y_{n+1}=y_n+hf(t_n,y_n)$$
so that we have an explicit formula again:
$$y_{n+1} = y_n + {h\over2} [f(t_n, y_n) + f(t_n + h, y_n + h f(t_n, y_n))]$$
This is known as Heun's method. It is one of the simplest of a class of methods called predictor-corrector algorithms (Euler's method is only a predictor method). In code:
@time for n=1:npts-1
tn=(n-1)*h-t0;
y[n+1]=y[n]+(h/2)*(f(tn,y[n])+f(tn+h,y[n]+h*f(tn,y[n])))
end
We can similarly compute the mean absolute error with this method:
hlist=[2.0^-k for k=1:26]
herror=[];
for h in hlist
npts=round(Int64,tmax/h);
y=0.0*collect(1:npts);
y[1]=-24/37;
@time for n=1:npts-1
tn=(n-1)*h;
y[n+1]=y[n]+(h/2)*(f(tn,y[n])+f(tn+h,y[n]+h*f(tn,y[n])))
end
append!(herror,mean(abs.([-(24/37)*cos(3t)-(4/37)*sin(3t) for t in ((1:npts).-1).*h]-y)))
end
this time on covid:
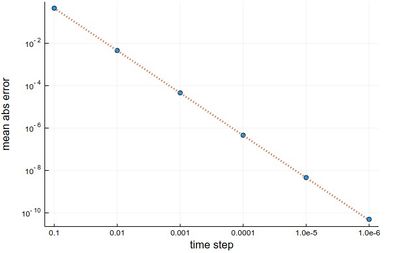
This is more resource intensive but now we get a much better $h^2$ error:
scatter(herror, xlabel="time step", ylabel="mean abs error",
xticks=(1:26, string.(hlist)), legend=false, yscale=:log10)
plot!(x->5*herror[1]*2.0^-(2x), 1, 25, ls=:dot, lw=3)
The same idea can be extended and we now present one of the most powerful predictor-corrector algorithms of all,
one which is so accurate that most computer algorithms use it as default: the fourth-order Runge-Kutta Method. RK methods are optimized predictor-corrector methods, so they push the idea of Heun's method to the top. The RK4 method finds the optimum correction-prediction (in a way which we do not detail here) to involve these intermediate points:
\begin{align}
k_1 &= h\ f(t_n, y_n)\,, \\
k_2 &= h\ f\left(t_n + \frac{h}{2}, y_n + \frac{k_1}{2}\right)\,, \\
k_3 &= h\ f\left(t_n + \frac{h}{2}, y_n + \frac{k_2}{2}\right)\,, \\
k_4 &= h\ f\left(t_n + h, y_n + k_3\right)\,,
\end{align}
and then the calculation is explicit:
\begin{align} t_{n+1} &= t_n + h\,, \\ y_{n+1} &= y_n + \tfrac{1}{6}\left(k_1 + 2k_2 + 2k_3 + k_4 \right)\,. \end{align}
In code:
@time for n=1:npts-1
tn=(n-1)*h-t0;
k1=h*f(tn,y[n]);
k2=h*f(tn+(h/2),y[n]+k1/2);
k3=h*f(tn+(h/2),y[n]+k2/2);
k4=h*f(tn+h,y[n]+k3);
y[n+1]=y[n]+(1/6)*(k1+2*k2+2*k3+k4)
end
The error analysis on the same problems as above now yields a very different result:
herror=[];
for h in hlist
npts=round(Int64,tmax/h);
y=0.0*collect(1:npts);
y[1]=-24/37;
@time for n=1:npts-1
tn=(n-1)*h;
k1=h*f(tn,y[n]);
k2=h*f(tn+(h/2),y[n]+k1/2);
k3=h*f(tn+(h/2),y[n]+k2/2);
k4=h*f(tn+h,y[n]+k3);
y[n+1]=y[n]+(1/6)*(k1+2*k2+2*k3+k4)
end
append!(herror,mean(abs.([-(24/37)*cos(3t)-(4/37)*sin(3t) for t in ((1:npts).-1).*h]-y)))
end
0.006093 seconds (3.91 k allocations: 64.688 KiB) 0.007069 seconds (41.92 k allocations: 674.766 KiB) 0.071775 seconds (437.74 k allocations: 6.871 MiB) 0.805397 seconds (4.40 M allocations: 68.998 MiB, 1.76% gc time) 6.734973 seconds (43.98 M allocations: 690.260 MiB, 1.41% gc time) 77.495034 seconds (439.82 M allocations: 6.741 GiB, 1.57% gc time)
scatter(herror, xlabel="time step", ylabel="mean abs error",
xticks=(1:6, string.(hlist)), legend=false, yscale=:log10)
plot!(x->10^4*herror[1]*10.0^-(4x), 1, 6, ls=:dot, lw=3, ylims=(10^-15,10^-3))
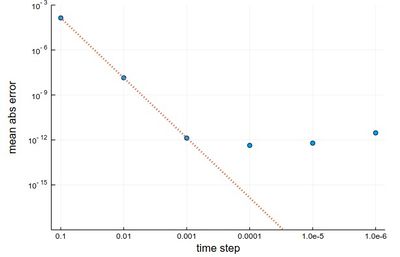
The gain from $h=0.001$ to $h=0.0001$ is marginally better, and for smaller still $h$, it actually becomes worse, due to rounding errors. It works so well that many, if not most, resources would use the RK4 to integrate ODE.
We now turn to the case of coupled equations, in which case the method reads
$$\vec y'=\vec f(t,\vec y)$$
where
$$ \vec y\equiv \begin{pmatrix}
y_1\\y_2
\end{pmatrix} \quad\text{and}\quad \vec f\equiv \begin{pmatrix}
f_1\\f_2
\end{pmatrix}\,. $$
The methods are the same as before just applying directly to the vectors instead. An interesting coupled system of ODE, namely, the Volterra-Lotka model of prey-predator interactions. This is modelled with the pair of coupled ODE:
\begin{align}
\frac{dx}{dt} &= \alpha x - \beta x y, \\
\frac{dy}{dt} &= \delta x y - \gamma y,
\end{align}
The functions are implemented as:
function f1(t,y1, y2)
α*y1-β*y1*y2
end
function f2(t,y1, y2)
δ*y1*y2-γ*y2
end
Some common initialization for all methods, in particular, we now need two arrays of values to store the evolution of $x$ (in y1) and $y$ (in y2):
tmax=100
h=.001
npts=round(Int,tmax/h)
y1=0.0*collect(1:npts);
y2=0.0*collect(1:npts);
y1[1]=1;
y2[1]=.1;
α=2/3;
β=4/3;
γ=1;
δ=1;
Euler's method in this case reads:
$$\vec y_{n+1}=\vec y_n+h\vec f(t_n,\vec y_n)$$
or, breaking down this equation componentwise:
$$\begin{align} y_{1,n+1}&=y_{1,n}+hf_1(t_n,y_{1,n},y_{2,n})\\ y_{2,n+1}&=y_{2,n}+hf_2(t_n,y_{1,n},y_{2,n}) \end{align}$$
In code:
@time for i=1:npts-1
y1[i+1]=y1[i]+h*f1((i-1)*h,y1[i],y2[i])
y2[i+1]=y2[i]+h*f2((i-1)*h,y1[i],y2[i])
end
Heun's version reads:
$$\vec y_{n+1}=\vec y_n+{h\over 2}\left(\vec f(t_n,\vec y_n)+\vec f(t_{n+1},\vec y_n+h\vec f(t_n,\vec y_n)\right)$$
or, breaking down this equation componentwise:
$$\begin{align}
y_{1,n+1} &= y_{1,n} + {h\over2} [f(t_n, y_{1,n}, y_{2,n}) + f(t_n + h, y_{1,n} + h f(t_n, y_{1,n}, y_{2,n}), y_{2,n})]\\
y_{2,n+1} &= y_{2,n} + {h\over2} [f(t_n, y_{1,n}, y_{2,n}) + f(t_n + h, y_{1,n}, y_{2,n} + h f(t_n, y_{1,n}, y_{2,n}))]
\end{align}$$
In code; where this time we'll find both more convenient and efficient to define auxiliary quantities, that are furthermore invoked more than once:
@time for n=1:npts-1
tn=(n-1)*h;
f1left=f1(tn,yH1[n],yH2[n])
f2left=f2(tn,yH1[n],yH2[n])
f1right=f1(tn+h,yH1[n]+h*f1left,yH2[n]+h*f2left)
f2right=f2(tn+h,yH1[n]+h*f1left,yH2[n]+h*f2left)
yH1[n+1]=yH1[n]+(h/2)*(f1left+f1right)
yH2[n+1]=yH2[n]+(h/2)*(f2left+f2right)
end
RK4's version reads:
$$ \begin{align} t_{n+1} &= t_n + h\,, \\ \vec y_{n+1} &= \vec y_n + \tfrac{1}{6}\left(\vec k_1 + 2\vec k_2 + 2\vec k_3 + \vec k_4 \right)\,. \end{align} $$
in terms of the intermediate quantities:
$$ \begin{align} \vec k_1 &= h\vec f(t_n, \vec y_n)\,, \\ \vec k_2 &= h\vec f\left(t_n + \frac{h}{2}, \vec y_n + \frac{\vec k_1}{2}\right)\,, \\ \vec k_3 &= h\vec f\left(t_n + \frac{h}{2}, \vec y_n + \frac{\vec k_2}{2}\right)\,, \\ \vec k_4 &= h\vec f\left(t_n + h, \vec y_n + \vec k_3\right)\,, \end{align} $$
In code
@time for n=1:npts-1
tn=(n-1)*h;
# Intermediate steps
k11=h*f1(tn,yRK1[n],yRK2[n]);
k12=h*f2(tn,yRK1[n],yRK2[n]);
k21=h*f1(tn+(h/2),yRK1[n]+k11/2,yRK2[n]+k12/2);
k22=h*f2(tn+(h/2),yRK1[n]+k11/2,yRK2[n]+k12/2);
k31=h*f1(tn+(h/2),yRK1[n]+k21/2,yRK2[n]+k22/2);
k32=h*f2(tn+(h/2),yRK1[n]+k21/2,yRK2[n]+k22/2);
k41=h*f1(tn+h,yRK1[n]+k31,yRK2[n]+k32);
k42=h*f2(tn+h,yRK1[n]+k31,yRK2[n]+k32);
# Real step
yRK1[n+1]=yRK1[n]+(1/6)*(k11+2*k21+2*k31+k41);
yRK2[n+1]=yRK2[n]+(1/6)*(k12+2*k22+2*k32+k42);
end
Results can be shown in two ways:
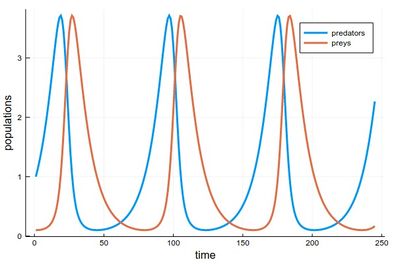
1 - As the respective solutions. This shows the oscillations of predators and preys
pRK=plot([[yRK1[i] for i=1:240], [yRK2[i] for i=1:240]],
lw=3, xlabel="time", ylabel="populations", label="RK4")
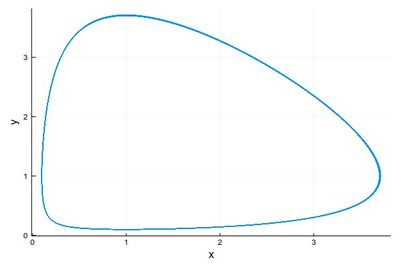
2 - As a phase-space solution, showing the simultaneous state of the system (here, ecosystem), with time as a parametric parameter:
psRK=plot([(yRK1[i], yRK2[i]) for i=1:npts],
lw=1, xlabel="x", ylabel="y", legend=false)
This comparing the three methods together (the various plots have been evaluated as pE, pH, etc.):
plot(pE,pH,pRK,psE,psH,psRK,layout=(2,3),dpi=150)
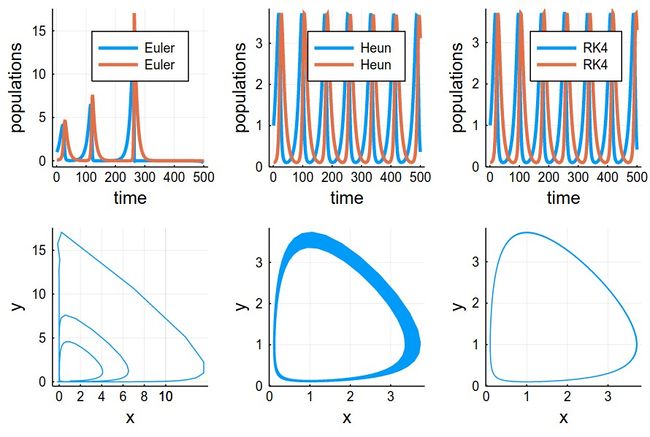
The time-evolutions at the top are over considerably fewer cycles for Heun & RK4 methods than those simulated to produce the phase space solutions, bottom. You can see how the RK4 method stays stable (which is the correct behavior) while the Heun method slowly drifts towards the stable point.
Links
- Compartmental models in epidemiology as a variation of Volterra-Lotka dynamics.
References
- The ultimate reference for this topic is Butcher, John C. (2003), Numerical Methods for Ordinary Differential Equations, New York: John Wiley & Sons, ISBN 978-0-471-96758-3.