Crash Course in Scientific Computing

XVII. Interpolation

Interpolation describes the general problem of providing the value of a function, which is known only for a few points, at any point which lies between other known points (if the unknown point is not "surrounded" by known points, then the problem becomes that of "extrapolation").

The simplest and also most natural method of interpolation is linear interpolation, which assumes that two neighboring points are linked by a line. It has been used since immemorial times throughout history and remains a basic technique in the computer industry, which even formed a special name for it, "lerp" (also used as a verb).

The method simply consists in finding the equation for a line between two points, those which are known from the data, i.e.,

$$L(x)=f(a)+{f(b)-f(a)\over b-a}(x-a)$$

Let us assume that in the parametrization of our problem, the range of the function is the number of equally-spaced data points known and we wish to interpolate to real-valued functions. All variations of lerp will do something similar. We can then refer to the known data points $a$ and $b$ from $x$ as:

$$ \begin{align} a&=\lfloor x\rfloor\\ b&=\lceil x\rceil \end{align} $$

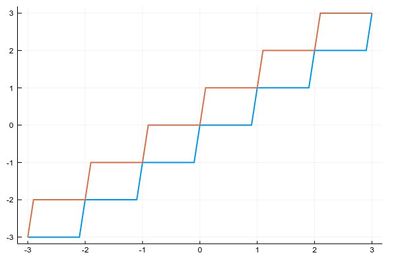
where the floor and ceil functions are defined as follows:

plot([floor, ceil], -3:.1:3, legend=false, lw=2)

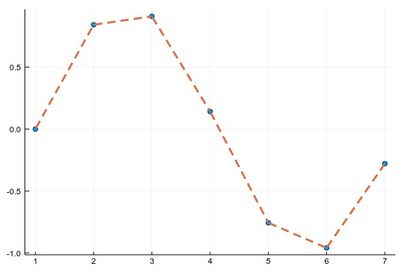
In this case, our linear interpolation is easily implemented. Here is some sample data:

data = [sin(i) for i=0:2pi]

And here is the function to "lerp" it:

function lerpdata(x)
    a=floor(Int,x);
    b=ceil(Int,x);
    data[a]+((data[b]-data[a])/(b-a))*(x-a)
end

scatter(data)
plot!(lerpdata,1:.01:7, lw=3, ls=:dash, legend=false)

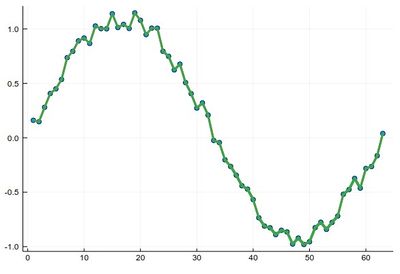
While it works well with enough points if the data has no noise, if it has, it gives disagreeable results:

data = [sin(i)+rand()/5 for i=0:.1:2pi]
scatter(data)
plot!(lerpdata,1:.0001:63, lw=3, legend=false)

In two dimensions, linear interpolation becomes bilinear interpolations (in 3D, trilinear, etc.)

We can go beyond lerp with polynomials, i.e., fitting with functions that are not straight lines but bring in the curviness of power functions.

A great choice of interpolating polynomials is the so-called Lagrange-interpolating polynomials, which provide the unique polynomial of order $n$ to pass by the $n$ points $(x_i, y_i)$ (with $1\le i\le n$). Note that the order of the polynomial is the same as the number of points one wishes to pass through. These polynomials are obtained as a linear superposition of the so-called Lagrange-basis polynomials:

$$\ell _{j}(x)\equiv\prod _{\begin{smallmatrix}1\leq k\leq n\\k\neq j\end{smallmatrix}}{\frac {x-x_{k}}{x_{j}-x_{k}}}={\frac {(x-x_{1})}{(x_{j}-x_{1})}}\cdots {\frac {(x-x_{j-1})}{(x_{j}-x_{j-1})}}{\frac {(x-x_{j+1})}{(x_{j}-x_{j+1})}}\cdots {\frac {(x-x_{n})}{(x_{j}-x_{n})}}$$

They are such that $\ell_j(x_k)=0$ for all $x_k$ with $1\le k\le n$ when $k\neq j$, otherwise $\ell_j(x_j)=1$. Concisely:

$$\ell_j(x_k)=\delta_{jk}\,.$$

The interpolating polynomial $P_f$ of the function $f$ sampled at the points $x_k$ is then obtained as a linear superposition of the Lagrange polynomials with the values of the function as the weighting coefficients:

$$P_f(x)=\sum_{j=1}^n f(x_j)\ell_j(x)$$

Given some points $(x_i, y_i)$, e.g.,

xi=[1, 2, 3, 5];
yi=[1, 3, 1, 2];

plot the Lagrange polynomials allowing to interpolate through all these points along with the interpolation polynomial itself. Your code should display something like this on the previous input:

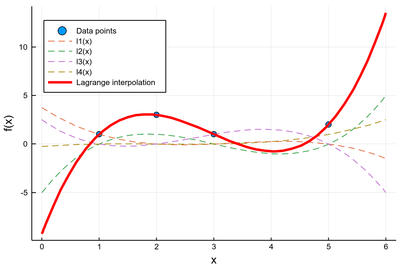
function plotLagrange(xi, yi)
    scatter((xi, yi), label="Data points", legend=:topleft);
    for j=1:length(xi)
        plot!(x->prod([(x-xi[k])/(xi[j]-xi[k])
                       for k∈union(1:j-1,j+1:length(xi))]),
              minimum(xi)-1, maximum(xi)+1, label="l$(j)(x)", ls=:dash)
    end
    plot!(x->sum([yi[j]*prod([(x-xi[k])/(xi[j]-xi[k])
                              for k∈union(1:j-1,j+1:length(xi))])
                  for j∈1:length(xi)]), minimum(xi)-1, maximum(xi)+1,
          lw=3, lc=:red, label="Lagrange interpolation", xlabel="x", ylabel="f(x)")
end

Runge's phenomenon is the interpolation version of the French saying «le mieux est l'ennemi du bien» (best is the enemy of the good): adding more interpolating points to some functions results in worst results.

Other polynomial schemes. We can name, for instance, Chebyshev Interpolation or Spline interpolation. We let these to your further inquiries.