m |
m (→VI. Numbers) |
||
| (4 intermediate revisions by one user not shown) | |||
| Line 2: | Line 2: | ||
== VI. Numbers == | == VI. Numbers == | ||
| − | {{ | + | {{quote|text=The device also functioned as an ordinary calculator, but only to a limited degree. It could handle any calculation which returned an answer of anything up to "4". |
| − | "1 + 1" it could manage ("2"), and "1 + 2" ("3") and "2 + 2" ("4") or "tan 74" ("3.4874145"), but anything above "4" it represented merely as "A Suffusion of Yellow". Dirk was not certain if this was a programming error or an insight beyond his ability to fathom. | + | "1 + 1" it could manage ("2"), and "1 + 2" ("3") and "2 + 2" ("4") or "tan 74" ("3.4874145"), but anything above "4" it represented merely as "A Suffusion of Yellow". Dirk was not certain if this was a programming error or an insight beyond his ability to fathom.|author=[[Douglas Adams]]|source=[[The long dark tea time of the soul]].|style={{opencite}}}} |
| − | + | ||
| − | [[Douglas Adams]] | + | |
| − | |}} | + | |
Numbers are ultimately what computers deal with, and their classification is a bit different than the one we have seen in Platonic [[Mathematics]] where we introduced the big family of numbers as $\mathbb{N}$, $\mathbb{Z}$, $\mathbb{Q}$, $\mathbb{R}$ and $\mathbb{C}$. The basic numbers are bits, which were the starting point of the course. We have seen already how integers derive from them by grouping several bits, basically changing from base 2 to base 10 or base 16 (hexadecimal). There is much more to the story, as can be seen from the following line of code we used in our definition of the Collatz sequence: | Numbers are ultimately what computers deal with, and their classification is a bit different than the one we have seen in Platonic [[Mathematics]] where we introduced the big family of numbers as $\mathbb{N}$, $\mathbb{Z}$, $\mathbb{Q}$, $\mathbb{R}$ and $\mathbb{C}$. The basic numbers are bits, which were the starting point of the course. We have seen already how integers derive from them by grouping several bits, basically changing from base 2 to base 10 or base 16 (hexadecimal). There is much more to the story, as can be seen from the following line of code we used in our definition of the Collatz sequence: | ||
| Line 207: | Line 204: | ||
The quickest and most natural way is to turn to another, wider type, namely, floats. These are important enough by themselves to require a dedicated attention. | The quickest and most natural way is to turn to another, wider type, namely, floats. These are important enough by themselves to require a dedicated attention. | ||
| − | Floats are the type of so-called "floating-point arithmetic", which is a somewhat poetic way to refer to decimal numbers, such as 1.4142135623730951 (a computer approximation to $\sqrt{2}$). | + | Floats are the type of so-called "floating-point arithmetic", which is a somewhat poetic way to refer to decimal numbers, such as 1.4142135623730951 (a computer approximation to $\sqrt{2}$). The terminology comes in opposition to [https://en.wikipedia.org/wiki/Fixed-point_arithmetic fixed-point arithmetic] where the "radix" (the decimal point) is pinned at the same position, while floating points allow it to move, to cover considerably wider ranges. Indeed, when dealing with such computer-abstraction of real numbers, one has to worry about the ''range'' (how far one can go in the big numbers $|x|\gg1$ and small numbers $|g|\ll1$) and ''precision'' (how accurate is our quantity or how many so-called "significant" numbers does it have). |
The widely accepted convention is that defined by the IEEE 754 double precision floating point number, which distributes the 64 bits of a float as follows: | The widely accepted convention is that defined by the IEEE 754 double precision floating point number, which distributes the 64 bits of a float as follows: | ||
| Line 225: | Line 222: | ||
** $2047\to 2^{-1023+2047}=2^{1024}\approx 2\times10^{308}$ | ** $2047\to 2^{-1023+2047}=2^{1024}\approx 2\times10^{308}$ | ||
** $2048\to $ special numbers: NaN and $\infty$. | ** $2048\to $ special numbers: NaN and $\infty$. | ||
| − | * The 52-bits mantissa (or significand, or precision), give the value which is to be scaled by the powers: | + | * The 52-bits mantissa (or significand, or precision, or fraction...), give the value which is to be scaled by the powers: |
$$(-1)^{\text{sign}}(1.b_{51}b_{50}...b_{0})_{2}\times 2^{\text{exponent}-1023}$$ | $$(-1)^{\text{sign}}(1.b_{51}b_{50}...b_{0})_{2}\times 2^{\text{exponent}-1023}$$ | ||
| Line 247: | Line 244: | ||
{{exstart}} | {{exstart}} | ||
Write Julia functions to convert decimal numbers—both integer or fractional—into their binary representation. ([[WLP_VI/Numbers/exbin|Answer]]) | Write Julia functions to convert decimal numbers—both integer or fractional—into their binary representation. ([[WLP_VI/Numbers/exbin|Answer]]) | ||
| + | {{exstop}} | ||
| + | |||
| + | {{exstart}} | ||
| + | Write a function to provide the decimal representation of a Float64 bit encoding, i.e., the reverse of the <tt>bitstring()</tt> function. ([[WLV_VI/Numbers/reversebitstring|Answer]]) | ||
{{exstop}} | {{exstop}} | ||
| Line 263: | Line 264: | ||
"0000000000000000000000000000000000000000000000000000000000000000" | "0000000000000000000000000000000000000000000000000000000000000000" | ||
</pre> | </pre> | ||
| + | |||
| + | There are curiosities in the encoding, like the existence of a negative zero, which is equal to zero but not in all operations: | ||
| + | |||
| + | <pre> | ||
| + | julia> bitstring(0.0) | ||
| + | "0000000000000000000000000000000000000000000000000000000000000000" | ||
| + | |||
| + | julia> bitstring(-0.0) | ||
| + | "1000000000000000000000000000000000000000000000000000000000000000" | ||
| + | |||
| + | julia> 0.0==-.00 | ||
| + | true | ||
| + | </pre> | ||
Now, if we would follow the convention, the smallest number next to zero would be: | Now, if we would follow the convention, the smallest number next to zero would be: | ||
| Line 277: | Line 291: | ||
<center><wz tip="">[[File:floats-nosubnormal.png|750px]]</wz></center> | <center><wz tip="">[[File:floats-nosubnormal.png|750px]]</wz></center> | ||
| − | One finds indeed by computing differences between consecutive floats that there is a gap of $2^n/2^{52}$ between consecutive numbers with the exponent $n$ or also between the largest number with power $n$ and the smallest number with power $n+1$, with, therefore, only a change of slope when changing powers. In contrast, when reaching the smallest possible numbers, one jumps abruptly to zero, the pattern being: | + | One finds indeed by computing differences between consecutive floats that there is a gap of $2^n/2^{52}$ between consecutive numbers with the exponent $n$ or also between the largest number with power $n$ and the smallest number with power $n+1$ <wz tip="The arithmetical difference between two consecutive representable floating-point numbers with the same exponent is called a unit in the last place (ULP).">(?!)</wz>, with, therefore, only a change of slope when changing powers. In contrast, when reaching the smallest possible numbers, one jumps abruptly to zero, the pattern being: |
$$0, 2^{-1023}, 2^{-1022}, 2^{-1021}, \cdots, 2^{1023}, 2^{1024}$$ | $$0, 2^{-1023}, 2^{-1022}, 2^{-1021}, \cdots, 2^{1023}, 2^{1024}$$ | ||
| Line 293: | Line 307: | ||
$$0, \color{red}{2^{-1074}, 2^{-1073}, \cdots, 2^{-1025}, 2^{-1024}}, 2^{-1023}, 2^{-1022}, 2^{-1021}, \cdots$$ | $$0, \color{red}{2^{-1074}, 2^{-1073}, \cdots, 2^{-1025}, 2^{-1024}}, 2^{-1023}, 2^{-1022}, 2^{-1021}, \cdots$$ | ||
| − | with all the powers $2^n$ with $-1074\le n\le 1024$ added. For the smallest ones, these are few numbers, namely only one for $2^{-1074}$ and $2^{-1073}$, two for $2^{-1072}$, four for $2^{-1071}$, etc., so this is filling the "end of the gap" fairly parsimoniously, but that still allows to hold to more stable calculations when involving very small numbers | + | with all the powers $2^n$ with $-1074\le n\le 1024$ (in red) added as compared to the normal encoding. For the smallest ones, these are few numbers, namely only one for $2^{-1074}$ and $2^{-1073}$, two for $2^{-1072}$, four for $2^{-1071}$, etc., so this is filling the "end of the gap" fairly parsimoniously, but that still allows to hold to more stable calculations when involving very small numbers. |
| − | * Smallest denormal number: $2^{-52}\times 2^{-1022}\approx 4.94\times10^{-324}$ (julia gives this as <tt>eps(0.0)</tt> that evaluates to <tt>5.0e-324</tt> | + | * Smallest denormal number: $2^{-52}\times 2^{-1022}\approx 4.94\times10^{-324}$ (julia gives this as <tt>eps(0.0)</tt> that evaluates to <tt>5.0e-324</tt>). |
* Largest denormal number: $\sum_{i=1}^{52}2^{-i}\times2^{-1022}\approx2.22\times10^{-308}$. | * Largest denormal number: $\sum_{i=1}^{52}2^{-i}\times2^{-1022}\approx2.22\times10^{-308}$. | ||
| − | * Smallest normal number: $ | + | * Smallest normal number: $2^{-1022}\approx2.22\times10^{-308}$ (and is only $\approx 4.94\times10^{-324}$ (i.e., smallest denormal number) larger than the largest denormal number. |
| + | |||
| + | Float64 thus describe correctly all integers whose absolute value is less than $2^{53}$. They can much beyond that but with some loss in precision, as illustrated by this ugly computer equation: | ||
| + | |||
| + | <pre> | ||
| + | julia> 2.0^53+1==2.0^53 | ||
| + | true | ||
| + | </pre> | ||
| + | |||
| + | The spacing there scaled to two full integers, so the statement becomes correct again (i.e., false) when asking for this larger separation: | ||
| + | |||
| + | <pre> | ||
| + | julia> 2.0^53+2==2.0^53 | ||
| + | false | ||
| + | </pre> | ||
| + | |||
| + | but we become blind again with larger numbers, that require big differences to be resolved as different: | ||
| + | |||
| + | <pre> | ||
| + | julia> 2.0^1023+2.0^970==2.0^1023 | ||
| + | true | ||
| + | |||
| + | julia> 2.0^1023+2.0^971==2.0^1023 | ||
| + | false | ||
| + | </pre> | ||
The functions <tt>prevfloat()</tt> and <tt>nextfloat()</tt> give the nearest floats around a given value. For instance, if you ever wondered what were the numbers closest to $\pi$, here you are (that's valid only for a computer): | The functions <tt>prevfloat()</tt> and <tt>nextfloat()</tt> give the nearest floats around a given value. For instance, if you ever wondered what were the numbers closest to $\pi$, here you are (that's valid only for a computer): | ||
| Line 312: | Line 350: | ||
</pre> | </pre> | ||
| − | Denormal numbers are appealing but they come with their problems. One is that involving exceptions to the rule, they are typically much slower to process than normal numbers. Another is that they do not have 53 bits of precision. The smallest denormal number is really one-bit accurate and dividing it by 2 results in exactly zero: | + | Denormal numbers are appealing but they come with their problems. One is that, involving exceptions to the rule, they are typically much slower to process than normal numbers (they require so-called microcode to overtake the native FPU processor, FPU is the floating-point unit). Another is that they do not have 53 bits of precision. The smallest denormal number is really one-bit accurate and dividing it by 2 results in exactly zero: |
<pre> | <pre> | ||
| Line 345: | Line 383: | ||
</pre> | </pre> | ||
| − | + | Such encoding of numbers by the computer are important to keep in mind when one encounters things like: | |
| − | + | ||
| − | + | ||
| + | <pre> | ||
julia> 0.1+0.2==0.3 | julia> 0.1+0.2==0.3 | ||
false | false | ||
</pre> | </pre> | ||
| − | + | which are due to the failure of Float64 to encode 0.3 consistently from the rules of computer arithmetic: | |
| − | + | <pre> | |
| + | julia> bitstring(0.1+0.2) | ||
| + | "0011111111010011001100110011001100110011001100110011001100110100" | ||
| − | + | julia> bitstring(0.3) | |
| − | + | "0011111111010011001100110011001100110011001100110011001100110011" | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
</pre> | </pre> | ||
| − | + | We will not study these in detail now but re-iterate our warning to keep in mind the way that floats are actually stored and encoded by the computer, and that they quickly depart from their ideal Mathematical abstractions. This is a difficulty that we will encounter over and over again. | |
| − | + | These are the real, hardware, computer numbers. One can also deal symbolically with higher-precision numbers, in fact, arbitrary-precision numbers. The shortcoming there is the resources, both in time and memory, that can become considerably larger than with native numbers. | |
| − | + | ||
| − | + | So coming back to our initial integer problem of figuring out how big is <tt>typemax(UInt128)</tt>, one way is to turn to floats, which can go very high. The conversion can be made by invoking a neutral float that doesn't change the result but changes the type: | |
<pre> | <pre> | ||
| − | julia> | + | julia> 1.0*0xffffffffffffffffffffffffffffffff |
| − | + | 3.402823669209385e38 | |
</pre> | </pre> | ||
| − | + | The other, more secure way to overcome Int64 is to turn to their generalization, known as BigInt (we're not counting in terms of bits anymore). This gives rise to this beautiful "computer equation": | |
<pre> | <pre> | ||
| − | julia> | + | julia> typemax(UInt128)==big(2)^128-1 |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
true | true | ||
| − | |||
| − | |||
| − | |||
</pre> | </pre> | ||
| − | + | (we could also use <tt>2^big(128)-1</tt>). This shows us that the biggest unsigned integer is, ''exactly'': | |
| − | + | ||
| − | + | ||
<pre> | <pre> | ||
| − | + | julia> 2^big(128)-1 | |
| − | + | 340282366920938463463374607431768211455 | |
| − | + | ||
| − | + | ||
| − | + | ||
</pre> | </pre> | ||
| − | + | or $340\,282\,366\,920\,938\,463\,463\,374\,607\,431\,768\,211\,455\approx 3.4\times10^{38}$ about 340 undecillion (just short of a duodecillion). Do we feel better now? At least, we know. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
=== Links === | === Links === | ||
Latest revision as of 08:02, 21 March 2021
Crash Course in Scientific Computing
VI. Numbers
The device also functioned as an ordinary calculator, but only to a limited degree. It could handle any calculation which returned an answer of anything up to "4". "1 + 1" it could manage ("2"), and "1 + 2" ("3") and "2 + 2" ("4") or "tan 74" ("3.4874145"), but anything above "4" it represented merely as "A Suffusion of Yellow". Dirk was not certain if this was a programming error or an insight beyond his ability to fathom.
Numbers are ultimately what computers deal with, and their classification is a bit different than the one we have seen in Platonic Mathematics where we introduced the big family of numbers as $\mathbb{N}$, $\mathbb{Z}$, $\mathbb{Q}$, $\mathbb{R}$ and $\mathbb{C}$. The basic numbers are bits, which were the starting point of the course. We have seen already how integers derive from them by grouping several bits, basically changing from base 2 to base 10 or base 16 (hexadecimal). There is much more to the story, as can be seen from the following line of code we used in our definition of the Collatz sequence:
if iseven(n)
n÷=2
else
n=3n+1
end
Note that we used integer division, which turns the even integer, e.g., 42, into another integer:
julia> 42÷2 21
Compare this to standard division:
julia> 42/2 21.0
The result looks the same, but these are actually different types of numbers and indeed, while one works as expected:
julia> iseven(42÷2) false
the other generates an error:
julia> iseven(42/2) ERROR: MethodError: no method matching iseven(::Float64) Closest candidates are: iseven(::Missing) at missing.jl:79 iseven(::Integer) at int.jl:91 Stacktrace: [1] top-level scope at none:0
Julia offers typeof() to tell us about the so-called "type" of the object:
julia> typeof(21) Int64 julia> typeof(21.0) Float64
That also works with other variables:
julia> typeof("hi")
String
julia> typeof('!')
Char
but today we are concerned with numbers. The different types refer to which set of values a variable of this type can take and how many bits are required to encode it. It can be Int (for integer, or whole number, a subset of $\mathbb{Z}$) in which case it can also be U (i.e., UInt) for unsigned (a subset of $\mathbb{N}$) or Float (for floating-point, or rational, a subset of $\mathbb{Q}$. The number of bits is given in the type: UInt128 is a signed integer with 128 bits and Float64 is floating-point with 64 bits. There are symbolic supports for higher types as we shall see later on.
Depending on the architecture of your microprocessor, the basic Int is defined as Int32 (32-bits architecture) or Int64. You can figure it out by asking:
julia> Int Int64
Even if you work on a 32-bits architecture, if you define numbers that don't fit in 32 bits, they will be encoded with 64 bits. If you go beyond 64 bits, you get an overflow:
julia> 2^64 0
The command bitstring() gives you how a number is encoded as bits. Here is the computer counting up to 3:
julia> [bitstring(i) for i∈0:3]
4-element Array{String,1}:
"0000000000000000000000000000000000000000000000000000000000000000"
"0000000000000000000000000000000000000000000000000000000000000001"
"0000000000000000000000000000000000000000000000000000000000000010"
"0000000000000000000000000000000000000000000000000000000000000011"
A lot of bits for nothing (1st line).
Julia by default use hexadecimal for unsigned integers:
a=0xa typeof(a)
You can convert that back into decimals by mixing with a neutral element (0 for addition, 1 for multiplication), but this changes the type:
julia> 1*0xa 10 julia> typeof(ans) Int64
The unsigned values of a variable range from $0$ to $2^{N}-1$ (the $-1$ because of $0$), while if it's signed, one bit must go to the sign information which reduces the range to $-2^{N-1}$ to $2^{N-1}-1$: there are more negative numbers than positive!
so the maximum value for the default integer (on a 64-bits architecture) is thus $2^{63}-1=9\,223\,372\,036\,854\,775\,807$ or about $9\times10^{18}$, nine quintillions. That's a bit number: a million million million, or a billion billion. We can get this number from:
julia> typemax(Int64) 9223372036854775807
or, equivalently:
julia> 2^63-1 9223372036854775807
If, however, we ask for
julia> 2^63 -9223372036854775808
This is called an overflow. On the positive side (no pun intended), UInt bring us farther but Julia encodes them in hexadecimal, understanding that if they have no signs, they behave as computer pointers, or addresses. Therefore:
julia> typemax(UInt) 0xffffffffffffffff
and
julia> 0xffffffffffffffff+1 0x0000000000000000
Overflow again, although there is a UInt128 type, the computer doesn't refer to them automatically. Unfortunately, it appears one can't force the machine to do it either, as still, not yet:
julia> x::UInt128=0xffffffffffffffff ERROR: syntax: type declarations on global variables are not yet supported
so one has to find a way out:
julia> 0x0ffffffffffffffff 0x0000000000000000ffffffffffffffff julia> typeof(0x0ffffffffffffffff) UInt128
in which case the arithmetics works again:
julia> 0x0ffffffffffffffff+1 0x00000000000000010000000000000000
at a cost to memory though:
julia> bitstring(0xffffffffffffffff) "1111111111111111111111111111111111111111111111111111111111111111" julia> bitstring(0x0ffffffffffffffff+1) "00000000000000000000000000000000000000000000000000000000000000010000000000000000000000000000000000000000000000000000000000000000"
How could we figure out which number is
julia> typemax(UInt128) 0xffffffffffffffffffffffffffffffff
There are several ways, including a cunning way: you can team up with the computer and get it yourself as twice the following (!?):
julia> typemax(Int128) 170141183460469231731687303715884105727
The quickest and most natural way is to turn to another, wider type, namely, floats. These are important enough by themselves to require a dedicated attention.
Floats are the type of so-called "floating-point arithmetic", which is a somewhat poetic way to refer to decimal numbers, such as 1.4142135623730951 (a computer approximation to $\sqrt{2}$). The terminology comes in opposition to fixed-point arithmetic where the "radix" (the decimal point) is pinned at the same position, while floating points allow it to move, to cover considerably wider ranges. Indeed, when dealing with such computer-abstraction of real numbers, one has to worry about the range (how far one can go in the big numbers $|x|\gg1$ and small numbers $|g|\ll1$) and precision (how accurate is our quantity or how many so-called "significant" numbers does it have).
The widely accepted convention is that defined by the IEEE 754 double precision floating point number, which distributes the 64 bits of a float as follows:

- The 1-bit sign is 0 for positive, 1 for negative. Simple (we started the course with this fact).
- The 11-bits exponent can take $2^{11}=2048$ values, with an offset of 1023 to cover both positive and negative powers:
- 0 subnormal numbers (explained below).
- $1\to 2^{-1023+1}=2^{-1022}\approx 2\times10^{-308}$
- $2\to 2^{-1023+2}=2^{-1021}\approx 4\times10^{-308}$
- ...
- $k$ with $1\le k\le2047\to 2^{-1023+k}$
- ...
- $1023\to 2^0=1$
- ...
- $2047\to 2^{-1023+2047}=2^{1024}\approx 2\times10^{308}$
- $2048\to $ special numbers: NaN and $\infty$.
- The 52-bits mantissa (or significand, or precision, or fraction...), give the value which is to be scaled by the powers:
$$(-1)^{\text{sign}}(1.b_{51}b_{50}...b_{0})_{2}\times 2^{\text{exponent}-1023}$$
or
$$\tag{1}(-1)^{\text{sign}}\left(1+\sum _{i=1}^{52}b_{52-i}2^{-i}\right)\times 2^{\text{exponent}-1023}$$
When encoding numbers in binary, there is an interesting oddity, which is that one gets a bit for free, namely, the leading bit, which is always 1 whatever the number (except for 0). Indeed, 0.75, for instance, is $7.5\times 10^{-1}$ in decimal floating-point notation and while it's the number 7 (that could have been 3 if this was 0.3) in base 10, in base 2, this always become 1 since by definition one brings the first one to leading figure, therefore it is always redundant (except if, again, for the one-number zero)
- $0.75\to 0.11_2=\left(1+{1\over2}\right)\times2^{-1}=1.1_2\times 2^{-1}$
- $0.375\to 0.011_2=\left(1+{1\over2}\right)\times2^{-2}=1.1_2\times 2^{-2}$
- $0.3125\to 0.0101_2=\left(1+{1\over2^2}\right)\times2^{-2}=1.01_2\times 2^{-2}$
- $\begin{align}0.00237&\to0.0000000010011011010100100000000001111101110101000100000100111_2\dots\\ &=\left(1+{1\over2^3}+{1\over2^4}+{1\over2^6}+{1\over2^7}+\dots+{1\over2^{50}}+{1\over2^{51}}+{1\over2^{52}}+c\dots\right)\times2^{-9}\\ &=1.0011011010100100000000001111101110101000100000100111\dots_2\times 2^{-9}) \end{align}$
Of course, this remains trivially true for numbers $>1$, so that finally, Eq. (1) has an extra free bit, and the encoding is really over 53 bits although only 52 are stored! Each exponent covers for the same number of $2^{52}$ numbers, but with a different range, with more numbers packed towards small numbers.
Write Julia functions to convert decimal numbers—both integer or fractional—into their binary representation. (Answer)
Write a function to provide the decimal representation of a Float64 bit encoding, i.e., the reverse of the bitstring() function. (Answer)
How about zero, though? This number doesn't fit in this normal scheme and so we have to "denormalize" it to include this much needed exception. This happens when:
- the exponent is zero
- the fraction is zero
then the number is 0 (or -0 if the sign bit is set). That's nice, right?
julia> bitstring(0) "0000000000000000000000000000000000000000000000000000000000000000" julia> bitstring(0.0) "0000000000000000000000000000000000000000000000000000000000000000"
There are curiosities in the encoding, like the existence of a negative zero, which is equal to zero but not in all operations:
julia> bitstring(0.0) "0000000000000000000000000000000000000000000000000000000000000000" julia> bitstring(-0.0) "1000000000000000000000000000000000000000000000000000000000000000" julia> 0.0==-.00 true
Now, if we would follow the convention, the smallest number next to zero would be:
- the exponent is still zero, meaning it is $2^{-1023}$.
- the fraction is 1 ($b_{0}=1$) as it'd make the number zero otherwise.
that makes, for the hypothetical smallest number:
$$1.(00\text{--51-zeros--}00)1\times 2^{-1023}=(1+2^{-52})\times2^{-1023}=1.11\times10^{-308}$$
which is very small, fine, but..., this makes a strange gap from zero!
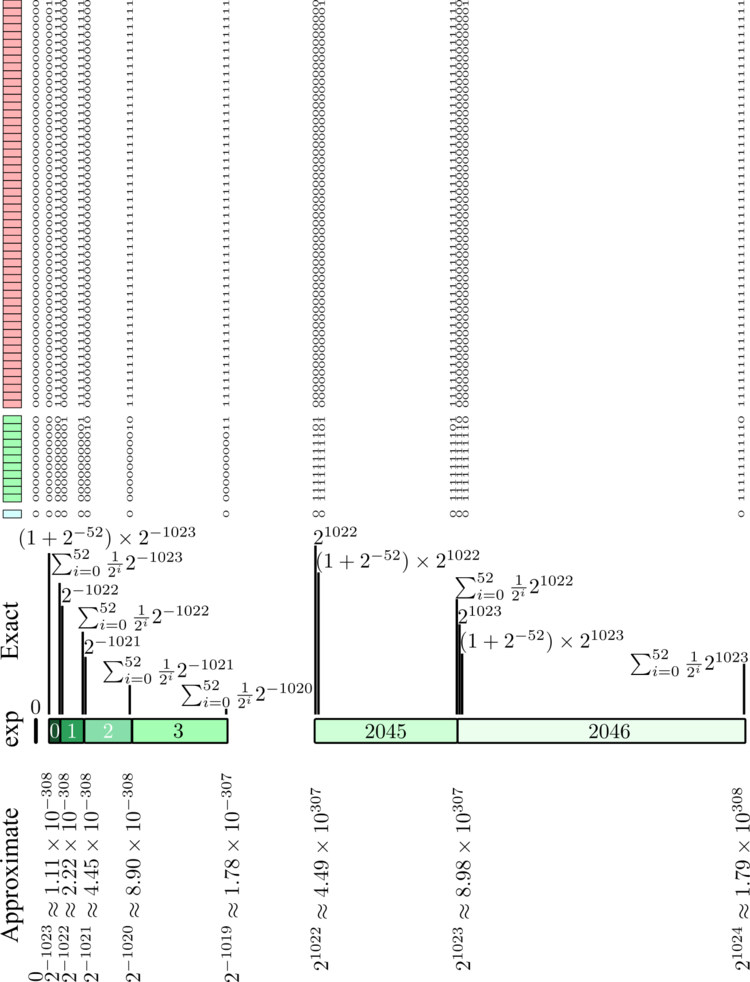
One finds indeed by computing differences between consecutive floats that there is a gap of $2^n/2^{52}$ between consecutive numbers with the exponent $n$ or also between the largest number with power $n$ and the smallest number with power $n+1$ (?!), with, therefore, only a change of slope when changing powers. In contrast, when reaching the smallest possible numbers, one jumps abruptly to zero, the pattern being:
$$0, 2^{-1023}, 2^{-1022}, 2^{-1021}, \cdots, 2^{1023}, 2^{1024}$$
This is the so-called "underflow" gap. To fill-this gap up, and allow for better calculations when manipulating small numbers from the float family, a different convention is used when the exponent is zero. Namely, the leading digit, always assumed to be there for so-called "normal" numbers, is then removed, and one goes directly to the encoding:
$$(-1)^{\text{sign}}\sum_{i=1}^{52}b_{52-i}2^{-i}\times 2^{\text{exponent}-1022}$$
where the exponent remains $-1022$, not $-1023$ as would have been the "normal" continuation (but we're denormal now!) This is such as to fill-up the gap nicely, as follows:
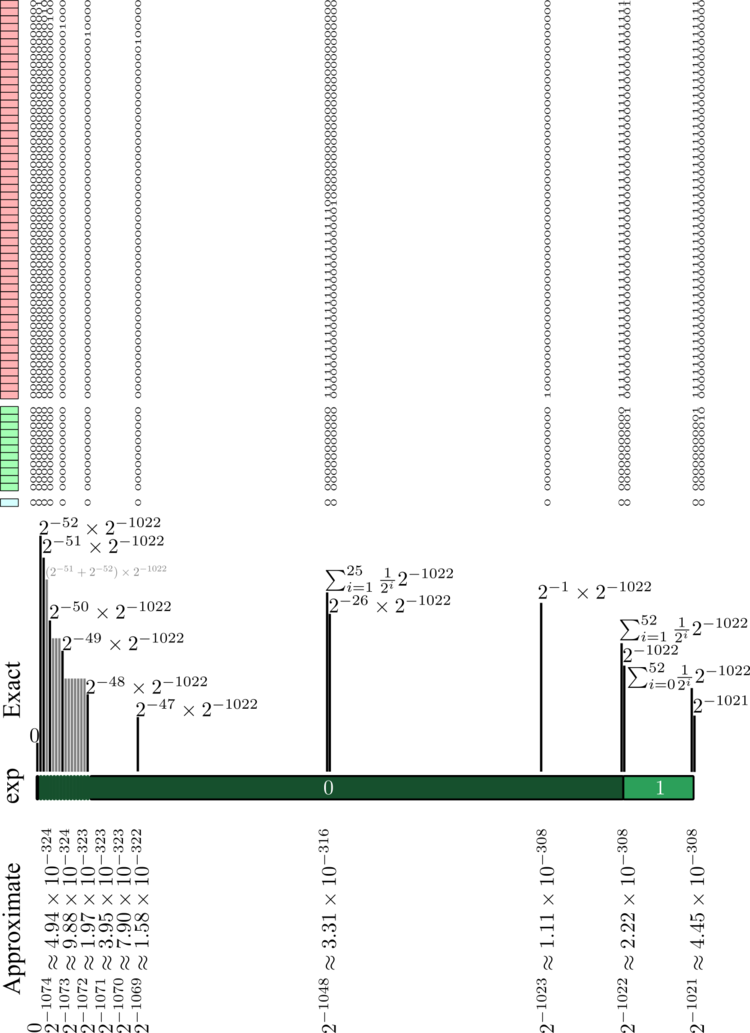
and we now have the sequence towards zero:
$$0, \color{red}{2^{-1074}, 2^{-1073}, \cdots, 2^{-1025}, 2^{-1024}}, 2^{-1023}, 2^{-1022}, 2^{-1021}, \cdots$$
with all the powers $2^n$ with $-1074\le n\le 1024$ (in red) added as compared to the normal encoding. For the smallest ones, these are few numbers, namely only one for $2^{-1074}$ and $2^{-1073}$, two for $2^{-1072}$, four for $2^{-1071}$, etc., so this is filling the "end of the gap" fairly parsimoniously, but that still allows to hold to more stable calculations when involving very small numbers.
- Smallest denormal number: $2^{-52}\times 2^{-1022}\approx 4.94\times10^{-324}$ (julia gives this as eps(0.0) that evaluates to 5.0e-324).
- Largest denormal number: $\sum_{i=1}^{52}2^{-i}\times2^{-1022}\approx2.22\times10^{-308}$.
- Smallest normal number: $2^{-1022}\approx2.22\times10^{-308}$ (and is only $\approx 4.94\times10^{-324}$ (i.e., smallest denormal number) larger than the largest denormal number.
Float64 thus describe correctly all integers whose absolute value is less than $2^{53}$. They can much beyond that but with some loss in precision, as illustrated by this ugly computer equation:
julia> 2.0^53+1==2.0^53 true
The spacing there scaled to two full integers, so the statement becomes correct again (i.e., false) when asking for this larger separation:
julia> 2.0^53+2==2.0^53 false
but we become blind again with larger numbers, that require big differences to be resolved as different:
julia> 2.0^1023+2.0^970==2.0^1023 true julia> 2.0^1023+2.0^971==2.0^1023 false
The functions prevfloat() and nextfloat() give the nearest floats around a given value. For instance, if you ever wondered what were the numbers closest to $\pi$, here you are (that's valid only for a computer):
julia> pi*1.0 3.141592653589793 julia> prevfloat(pi*1.0) 3.1415926535897927 julia> nextfloat(pi*1.0) 3.1415926535897936
Denormal numbers are appealing but they come with their problems. One is that, involving exceptions to the rule, they are typically much slower to process than normal numbers (they require so-called microcode to overtake the native FPU processor, FPU is the floating-point unit). Another is that they do not have 53 bits of precision. The smallest denormal number is really one-bit accurate and dividing it by 2 results in exactly zero:
julia> eps(0.0)/2.0 0.0
Compare with normal numbers:
julia> floatmin() 2.2250738585072014e-308 julia> issubnormal(ans) false julia> floatmin()/2 1.1125369292536007e-308 julia> issubnormal(ans) true
One should not confuse the smallest number the computer can assume with the so-called machine-epsilon, which is the precision of the significant, so $\approx 2^{-52}\approx 2.2\times10^{-16}$. This is given by eps() or found by the machine with this simple algorithm:
epsilon = 1.0;
while (1.0 + 0.5 * epsilon) ≠ 1.0
epsilon = 0.5 * epsilon
end
Such encoding of numbers by the computer are important to keep in mind when one encounters things like:
julia> 0.1+0.2==0.3 false
which are due to the failure of Float64 to encode 0.3 consistently from the rules of computer arithmetic:
julia> bitstring(0.1+0.2) "0011111111010011001100110011001100110011001100110011001100110100" julia> bitstring(0.3) "0011111111010011001100110011001100110011001100110011001100110011"
We will not study these in detail now but re-iterate our warning to keep in mind the way that floats are actually stored and encoded by the computer, and that they quickly depart from their ideal Mathematical abstractions. This is a difficulty that we will encounter over and over again.
These are the real, hardware, computer numbers. One can also deal symbolically with higher-precision numbers, in fact, arbitrary-precision numbers. The shortcoming there is the resources, both in time and memory, that can become considerably larger than with native numbers.
So coming back to our initial integer problem of figuring out how big is typemax(UInt128), one way is to turn to floats, which can go very high. The conversion can be made by invoking a neutral float that doesn't change the result but changes the type:
julia> 1.0*0xffffffffffffffffffffffffffffffff 3.402823669209385e38
The other, more secure way to overcome Int64 is to turn to their generalization, known as BigInt (we're not counting in terms of bits anymore). This gives rise to this beautiful "computer equation":
julia> typemax(UInt128)==big(2)^128-1 true
(we could also use 2^big(128)-1). This shows us that the biggest unsigned integer is, exactly:
julia> 2^big(128)-1 340282366920938463463374607431768211455
or $340\,282\,366\,920\,938\,463\,463\,374\,607\,431\,768\,211\,455\approx 3.4\times10^{38}$ about 340 undecillion (just short of a duodecillion). Do we feel better now? At least, we know.
Links
- Historical account of floating points numbers.
- What Every Computer Scientist Should Know About Floating-Point Arithmetic
- Post by Ciro Santilli on Stackoverflow (for Float32).
- Blog post on denormal numbers.
- A Float32 Converter.
- Integers & floats on docs.julialang.org.