m |
m |
||
| Line 148: | Line 148: | ||
$$P_f(x)\equiv\sum_{j=-2}^2f(x_j)\ell_j(x)$$ | $$P_f(x)\equiv\sum_{j=-2}^2f(x_j)\ell_j(x)$$ | ||
| + | |||
| + | The Lagrange polynomial remains, after all, a polynomial, so its derivative is in principle straightforward. | ||
| + | |||
| + | {{exstart}} | ||
| + | Show that the derivative of the Lagrange polynomial is given by: | ||
| + | |||
| + | $${\ell_{j}'(x)=\sum_{i\neq j}\left[{\frac {1}{x_{j}-x_{i}}}\prod_{m\neq i,j}{\frac {x-x_{m}}{x_{j}-x_{m}}}\right]}\label{eq:diffellj}$$. | ||
| + | |||
| + | Write a piece of code to plot these derivatives and check it against numerical differentiation of the Lagrange polynomials. | ||
| + | {{anstart}} | ||
| + | The calculation simplifies a lot by taking the logarithm of both sides: | ||
| + | \begin{equation} | ||
| + | \ln\ell_{j}(x)=\sum_{k\neq j}\ln{x-x_k\over x_j-x_k} | ||
| + | \end{equation} | ||
| + | |||
| + | in which case the products turns into a trivial sum of linear functions: | ||
| + | |||
| + | \begin{equation} | ||
| + | \left(\ln\ell_{j}(x)\right)'={\ell_j(x)'\over\ell_j(x)}=\sum_{k\neq j}\left(\ln{x-x_k\over x_j-x_k}\right)' | ||
| + | =\sum_{k\neq j}{1\over x-x_k}\,. | ||
| + | \end{equation} | ||
| + | |||
| + | so that the result is obtained immediately as: | ||
| + | |||
| + | \begin{equation} | ||
| + | \ell_j(x)'=\ell_j(x)\sum_{k\neq j}{1\over x-x_k} | ||
| + | \end{equation} | ||
| + | {{anstop}} | ||
| + | {{exstop}} | ||
and thus, its derivative is: | and thus, its derivative is: | ||
| Line 153: | Line 182: | ||
$$P_f(x)'\equiv\sum_{j=-2}^2f(x_j)\sum_{i\neq j}\left[{\frac {1}{x_{j}-x_{i}}}\prod_{m\neq i,j}{\frac {x-x_{m}}{x_{j}-x_{m}}}\right]$$ | $$P_f(x)'\equiv\sum_{j=-2}^2f(x_j)\sum_{i\neq j}\left[{\frac {1}{x_{j}-x_{i}}}\prod_{m\neq i,j}{\frac {x-x_{m}}{x_{j}-x_{m}}}\right]$$ | ||
| − | |||
| − | |||
By working out how to cancel the next-order terms, we arrive at the so-called [https://en.wikipedia.org/wiki/Five-point_stencil Five-point stencil]: | By working out how to cancel the next-order terms, we arrive at the so-called [https://en.wikipedia.org/wiki/Five-point_stencil Five-point stencil]: | ||
Revision as of 10:48, 19 March 2021
Crash Course in Scientific Computing
XIV. Derivatives
We now turn to the reverse process of last lecture's topic (it was on integrals), i.e., derivation. While in pure (pen-and-paper) Maths, differentiation is typically easier than integration, numerically, the difficulty is reversed. This is because integration as summing patches of the functions works well with basic continuity properties (e.g., not be discontinuous) while differentiation requires stronger properties, in particular the so-called Lipschitz continuity that limits how fast the function, even though continuous, can change. It also is very fragile to dividing by small numbers although a fairly recent "hack" against has been proposed by making a detour into the complex plane, as we shall see.
The basic idea behind differentiation comes from Taylor expansion:
\begin{equation} \tag{1} f(x\pm\epsilon)=f(x)\pm\epsilon f'(x)+{\epsilon^2\over2} f''(x)\pm{\epsilon^3\over6} f'''(x)+o(\epsilon^4) \end{equation}
that we wrote for both $\pm\epsilon$, and using the $o$-notation to mean that terms we neglected are of the order of $\epsilon^4$. From this, one can get the most obvious and natural numerical approximation for the derivative
$$f'(x)\approx\pm{f(x\pm\epsilon)-f(x)\over\epsilon}+o(\epsilon)$$
meaning we can expect an error of the order of $\epsilon$ with this method (namely $\approx{\epsilon\over 2}f''(x)$). We also see here one problem of numerical derivatives, which is that they imply dividing by a small number $h$, which is notoriously unstable and problematic. On the other hand, the numerator itself is a simple, so-called finite difference. We can use the diff command to computes finite differences:
diff(1:.5:10)
returns an array of 18 elements, all equal to 0.5. In this way, it is easy to compute a finite-difference derivative:
plot(diff([sin(pi*x) for x=0:.01:1])./.01)
This is a cosine. Importantly for numerical methods, one should look for simple tricks that maximise numerical accuracies. Observe, indeed, how one can sneakily cancel the $\epsilon^2$ term from (1) by subtracting $f(x-\epsilon)$ from $f(x+\epsilon)$:
$$f(x+\epsilon)-f(x-\epsilon)=2\epsilon f'(x)+{\epsilon^3\over 3}{f'''(x)}+o(\epsilon^3)$$
so that we have a much better approximation by computing with this slight variation:
$$f'(x)={f(x+\epsilon)-f(x-\epsilon)\over 2\epsilon}+o(\epsilon^2)$$
since $\epsilon^2\ll\epsilon$. The computational cost is the same, the numerical gain is considerable. Let's write a function. We'll it call Dl for "Differentiate list":
function Dl(f, δx, method="central") if method=="left" diff(f)/δx elseif method=="central" [f[i+1]-f[i-1] for i=2:length(f)-1]/(2*δx) end end
Let us compare the two methods for
δx=0.01; mysin=[sin(pi*x) for x in 0:δx:1]
We find fairly identical-looking results:
plot([Dl(mysin,δx,"central"), Dl(mysin,δx,"left")], legend=false)
The above comparison is actually not quite correct since the lists are of different size: the left method removes one point (the last one) while the central method removes two (the first and the last one), so they shouldn't be simply overlapped but also aligned; the difference would become significative with larger steps:
δx=0.1; plot([((δx:δx:1-δx), Dl(mysin,δx,"central")), ((0:δx:1-δx), Dl(mysin,δx,"left"))], legend=false) plot!(x-> pi*cos(pi*x), 0:.01:1, lc=:red, ls=:dashdotdot, la=.5, lw=3, xlabel="x", ylabel="sin(pi x)'", label="exact", dpi=200)
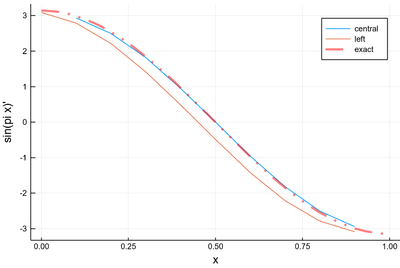
Derivatives of $\sin(pi x)$ with a large step: the central method is incredibly accurate!
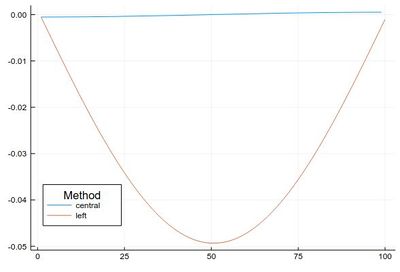
Even with a small step, δx=0.01, this error is actually quite large if looked at properly:
plot([ Dl(mysin,δx,"central")-[pi*cos(pi*i) for i in δx:δx:1-δx], Dl(mysin,δx,"left")-[pi*cos(pi*i) for i in 0:δx:1-δx] ], legendtitle="Method", legend=:bottomleft, label=["central" "left"])
One is also often interested in higher-order derivative. One would be tempted in using iterated derivations, which is, after all, the mathematical definition: $f''=(f')'$, so:
Dl(Dl(mysin, δx), δx)
That would work but it is better to implement this iteration at the core of the numerical method, rather than to iterate it from the outset, which will accumulate errors and multiply the number of operations. Here is a simple (also central) finite-difference formula:
$$f''(x)\approx={\frac {{\frac {f(x+h)-f(x)}{h}}-{\frac {f(x)-f(x-h)}{h}}}{h}}={\frac {f(x+h)-2f(x)+f(x-h)}{h^{2}}}$$
that we can implement as:
function Dl(f, δx, method="central", n=1) if n==1 if method=="left" diff(f)/δx elseif method=="central" [f[i+1]-f[i-1] for i=2:length(f)-1]/(2*δx) end elseif n==2 if method=="central" [f[i+1]-2f[i]+f[i-1] for i=2:length(f)-1]/(δx^2) else println("Sorry, method not available.") end end end
which both give apparently similar-looking results:
bigsin=[sin(x) for x in 0:δx:2pi] plot([Dl(Dl(bigsin, δx), δx), Dl(bigsin, δx, "central", 2)], label=["(f')'" "f''"], legend=:topleft)
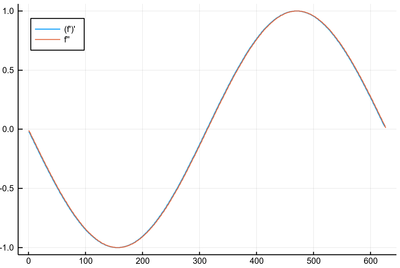
The error, in this case, is not very dramatic but it is significantly still better to use the second-order derivative once:
julia> plot([Dl(Dl(bigsin, δx), δx)-[-sin(x) for x in 0:δx:2pi-4δx], Dl(bigsin, δx, "central", 2)-[-sin(x) for x in 0:δx:2pi-2δx]], label=["(f')'" "f''"], ylabel="error")
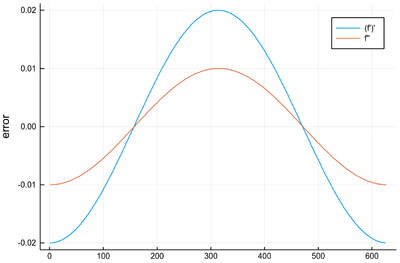
This idea of finding how to best combine finite differences of the function to approximate with the smallest possible error its derivative to a given order can be generalized in a similar way than we did for integration, namely, using Lagrange interpolation polynomials. We will apply it directly to a 5-order polynomial as lowest orders reproduce the results we already got from direct methods:
Show that derivating Lagrange polynomials to order 2, 3 and 4 reproduce finite-difference results in different combinations (e.g., forward).
We use, therefore, the five points $x_j$ with integer $j$ such that $-2\le j\le j$ and we shall look at the central method, which is the most common, so taking eventually $x=x_0$. For any $x$, the interpolation to order 5 reads:
$$P_f(x)\equiv\sum_{j=-2}^2f(x_j)\ell_j(x)$$
The Lagrange polynomial remains, after all, a polynomial, so its derivative is in principle straightforward.
Show that the derivative of the Lagrange polynomial is given by:
$${\ell_{j}'(x)=\sum_{i\neq j}\left[{\frac {1}{x_{j}-x_{i}}}\prod_{m\neq i,j}{\frac {x-x_{m}}{x_{j}-x_{m}}}\right]}\tag{2}$$.
Write a piece of code to plot these derivatives and check it against numerical differentiation of the Lagrange polynomials.
The calculation simplifies a lot by taking the logarithm of both sides: \begin{equation} \ln\ell_{j}(x)=\sum_{k\neq j}\ln{x-x_k\over x_j-x_k} \end{equation}
in which case the products turns into a trivial sum of linear functions:
\begin{equation} \left(\ln\ell_{j}(x)\right)'={\ell_j(x)'\over\ell_j(x)}=\sum_{k\neq j}\left(\ln{x-x_k\over x_j-x_k}\right)' =\sum_{k\neq j}{1\over x-x_k}\,. \end{equation}
so that the result is obtained immediately as:
\begin{equation} \ell_j(x)'=\ell_j(x)\sum_{k\neq j}{1\over x-x_k} \end{equation}
and thus, its derivative is:
$$P_f(x)'\equiv\sum_{j=-2}^2f(x_j)\sum_{i\neq j}\left[{\frac {1}{x_{j}-x_{i}}}\prod_{m\neq i,j}{\frac {x-x_{m}}{x_{j}-x_{m}}}\right]$$
By working out how to cancel the next-order terms, we arrive at the so-called Five-point stencil:
$$f'(x) \approx \frac{-f(x+2\epsilon)+8 f(x+\epsilon)-8 f(x-\epsilon)+f(x-2\epsilon)}{12\epsilon}$$
which we can add to our function:
function Dl(f, δx, method="central") if method=="left" diff(f)/δx elseif method=="central" [f[i+1]-f[i-1] for i=2:length(f)-1]/(2*δx) elseif method=="fivepoints" [-f[i+2]+8f[i+1]-8f[i-1]+f[i-2] for i=3:length(f)-2]/(12*δx) end end
Comparing their errors:
plot([ Dl(mysin,δx,"fivepoints")-[pi*cos(pi*i) for i in 2δx:δx:1-2δx], Dl(mysin,δx,"central")-[pi*cos(pi*i) for i in δx:δx:1-δx], Dl(mysin,δx,"left")-[pi*cos(pi*i) for i in 0:δx:1-δx] ], legendtitle="Method", legend=:bottom, label=["5 points" "central" "left"], ylims=(-.005,.001))
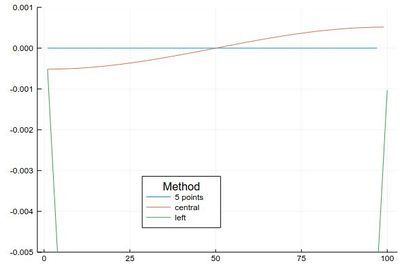
If we want a more quantitative study at the errors, we can look at how it scales for various $\epsilon$. This will allow us to look at logarithmic steps:
lδx=[10.0^(-k) for k in 1:7] err1=[mean(abs.(Dl([sin(pi*x) for x in 0:δx:1], δx, "left")-[pi*cos(pi*x) for x in 0:δx:1-δx])) for δx in lδx] err2=[mean(abs.(Dl([sin(pi*x) for x in 0:δx:1], δx, "central")-[pi*cos(pi*x) for x in δx:δx:1-δx])) for δx in lδx] err3=[mean(abs.(Dl([sin(pi*x) for x in 0:δx:1], δx, "fivepoints")-[pi*cos(pi*x) for x in 2δx:δx:1-2δx])) for δx in lδx] plot([abs.(err1) abs.(err2) abs.(err3)], yscale=:log10, label=["left" "central" "5 points"], xlabel="10^-k step", ylabel="Mean abs error", lc=[:red :blue :green]) plot!([x->10.0^(-x) x->10.0^(-2x) x->10.0^(-4x)],1,7, yscale=:log10, ylims=(10^(-15),1), lc=[:red :blue :green], ls=:dash, label=["" "" ""])
with the beautiful result:
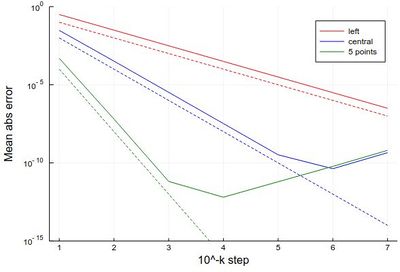
As one can see, the best method worsens for $\epsilon<10^{-4}$ so it will actually work better (and faster) for not too small an $\epsilon$.