Revision as of 16:27, 1 March 2021

Crash Course in Scientific Computing

7. Algorithms: the idea

An algorithm is a recipe to solve a problem with a computer, a list of instructions for the later to follow that will bring it to the solution, which it can duly report. Problems are of all types, from scientific problems such as finding roots of complex functions to integrating differential equations passing by everybody's daily problems such as finding the shortest or best route to bring you from A to B in a complex map or sorting the list of top results in an internet query. The set of instructions can be efficient and lead to a rapid, accurate and faithful solution from the computer, or on the opposite, clumsy, redundant and leading it to waste resources and possibly not even the best, or a good, or even any solution at all. The art of finding a good algorithm has been guiding scientists and engineers since antiquity. Any single problem typically comes with a myriad of different algorithms. For many problems, such as integer factorization, we do not have yet, and probably will never have, good algorithms which can perform the job in a reasonable time. This is the basis for today's cryptography.

One of the simplest algorithms is to find the largest number in a list that has no particular order. We will use this as a starting point to illustrate the above concepts. It is a simple algorithm because its best implementation is basically what one would do anyway: go through each element in turn, if the element we currently examine is larger than the largest we found so far, we update our record, if not, we carry on. Here's a Julia implementation:

function myfindmax(lst)
    i=1;
    imax=length(lst);
    lmax=lst[1]
    while i<imax
    i+=1;
        if lst[i]>lmax
            lmax=lst[i]
        end
    end
    lmax
end

Example application:

julia> myfindmax(rand(10))
0.985052934036265

Although in principle it is better to test your algorithm on cases which you know and that you can check yourself by hand:

julia> known=rand(Int8, 5)
5-element Array{Int8,1}:
 -13
 -94
  22
  90
 -86
 
julia> myfindmax(known)
90
 
julia> myfindmax(abs.(known))
94

It is also good to test on particular as well as extreme cases, e.g., when the max element is first or last. For instance, if we would have specified the increment i+=1 after the test, the algorithm would fail if the max would find itself as the last element of the array (which would be the case if the list would be ordered):

julia> myfindmax([i for i=1:10])
10

An important aspect of algorithms is their efficiency, how fast and good they are in performing the job. To benchmark, one can use @time or, if wanting to store the result for later processing, @elapsed (!!):

julia> mytime=zeros(100);
julia> for i=1:100
           lst = rand(10^6)
           mytime[i] = @elapsed myfindmax(lst);
       end
 
julia> comptime=zeros(100);
julia> for i=1:100
           lst = rand(10^6)
           comptime[i] = @elapsed maximum(lst);
       end
 
julia> plot([mytime comptime], label=["us" "julia"])

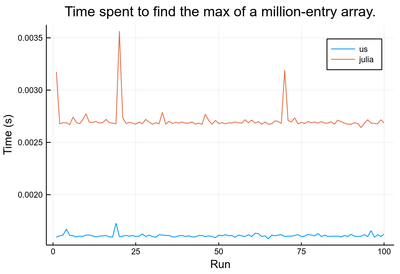
As an exception to the general rule, we find here that our own implementation is actually faster than the one provided by the system:

julia> mean(mytime)
0.0016102164000000002
 
julia> mean(comptime)
0.0027113203900000003

The "complexity" of our find-max algorithm is linear: it grows in direct proportion to the size of the input, as can be understood easily from the way the algorithm is designed. Here is this relationship explictely calculated by the computer:

julia>  lt=[@elapsed myfindmax(rand(10^i)) for i=1:8]
julia> scatter(lt, yscale=:log10, xlabel="10^n numbers", ylabel="Time (s)",
 title="Finding maximum in a list", legend=false)

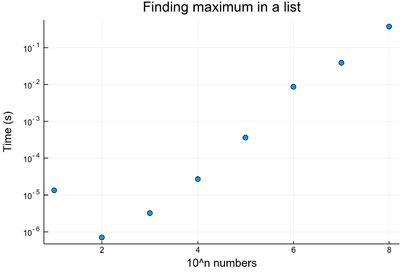
To do even more advanced benchmarking, one can be

julia> using BenchmarkTools

julia> @benchmark myfindmax(rand(10^6))
BenchmarkTools.Trial: 
  memory estimate:  7.63 MiB
  allocs estimate:  2
  --------------
  minimum time:     2.015 ms (0.00% GC)
  median time:      2.061 ms (0.00% GC)
  mean time:        2.184 ms (4.24% GC)
  maximum time:     42.876 ms (88.56% GC)
  --------------
  samples:          2285
  evals/sample:     1
 
julia> @benchmark maximum(rand(10^6))
BenchmarkTools.Trial: 
  memory estimate:  7.63 MiB
  allocs estimate:  2
  --------------
  minimum time:     3.344 ms (0.00% GC)
  median time:      3.461 ms (0.00% GC)
  mean time:        3.570 ms (3.05% GC)
  maximum time:     44.792 ms (91.19% GC)
  --------------
  samples:          1399
  evals/sample:     1

The fact that our readily-made version is faster than the one provided by the system has been flagged by the Julia community and has been traced to time being lost when checking for NaN numbers.

Algorithms usually rely on tricks or clever observations. For instance, whatever the numbers $y$ and $x$, it is always true that $\sqrt{x}$ is comprised between $y$ and $x/y$. This is easy to prove and follow from the fact that $1/\sqrt{x}=\sqrt{x}/x$. If $y<\sqrt{x}$, then $1/y>\sqrt{x}/x$ which brings us to

$$y<\sqrt{x}<x/y$$

while if $y>\sqrt{x}$ then, similarly, $1/y<\sqrt{x}/x$ and we have the opposite inequality

$$x/y<\sqrt{x}<y$$

So given to numbers $x$ and $y$, a good guess to approximate $\sqrt{x}$ is to take their average ${1\over2}(y+x/y)$. We now have a number closer to $\sqrt{x}$, so we can simply iterate. This is, thus, our algorithm, start with any $y_0\neq x$ and compute:

$$y_{n+1}={1\over2}\left(y_n+{x\over y_n}\right)$$

This will converge to $\sqrt{x}$. This method was known to the Babylonians to compute $\sqrt{2}$. This is the Julia code:

julia> x=2; y=1;
julia> while abs(y^2-x)>10^-12
           global y=(1/2)*(y+x/y)
           println(y)
       end
1.5
1.4166666666666665
1.4142156862745097
1.4142135623746899
1.414213562373095
 
julia> √2
1.4142135623730951

This is frustratingly fast! Numerical analysis shows that the number of significant digits doubles at each step. We don't need any better algorithm than this one designed by the Babylonians, and this is actually the steps that are undertaken by your pocket calculator, or any computer for that matter, when you press the √ button. Wherever it starts from, in just a few steps, it will have all the decimals of its accuracy correct to the sought square root. So now you how this happens. Let us see other implementations of important operations.

Sieve of Eratosthenes

Find the largest prime below $10^9$ and which number is it in the list of primes?Which one is next? Compare to the prime-counting function $\pi(x)$ that counts how many primes are there below $x$ and which Gauss approximated to $x/\ln(x)$.

Answer: This is $999\,999\,937$, the $50\,847\,534$th prime number, for which the prime-counting function $\pi(x)$ compares to Gauss' approximation $\pi(x)\approx x/\ln x=48\,254\,942$ to withing 5% accuracy. The next prime is $1\,000\,000\,007$.

Division algorithm/Euclidean algorithm

Euclidean—or integer—division takes two (positive, without loss of generality) integers $a$ (numerator) and $b$ (denominator) and returns another two integers: $q$ (quotient) and $r$ (remainder)

$$a=bq+r$$

with $0\ge q<p$. We have seen that julia computes these quantities directly so there is no need of an algorithm per se:

julia> function juliadiv(a,b)
           [a÷b, a%b]
       end

but to illustrate the point, let us look at various implementations. The oldest one is from Euclid himself, in his Elements, Book VII, Proposition 1, a simple method is proposed: starting with $r=a$, while $r\ge b$, subtract $b$ from $r$ and take this as the new $r$ and when this is not possible, what is left is the final remainder $r$. The number of times it took to get there is $q$. In julia code:

function eucliddiv(a,b)
    r=a
    q=0
    while r-b ≥ 0
        q+=1
        r=r-b
    end
    [q r]
end

This is very simple but can get quite lengthy. One would use long division algorithms for faster results. Instead of looking at those now, we turn to an important historical algorithm, Euclid's algorithm, which computes the gcd (greatest common divisor between two numbers). This is one of the oldest known algorithms. It is based one the fact that the gcd of two numbers is the same as the gcd of the smaller number with the positive difference of the numbers, so that by iterations, one can decrease the values of the numbers until they become equal, at which point the value thus found is the gcd. This is a julia implementation:

function euclidgcd(a,b)
    while a!=b
        if a > b
            a = a-b
        elseif a < b
            b = b-a
        end
    end
    a
end

This is the result, showing the details of the intermediate steps:

function euclidgcd(a,b)
    i=0;
    while a!=b
        if a > b
            a = a-b
        elseif a < b
            b = b-a
        end
        i+=1;
        println("step $(i):  a=$(a) b=$(b)")
    end
    a
end

julia> a=abs(rand(Int))
3371149190952905360
 
julia> b=4884762153376862325
4884762153376862325
 
step 1:  a=3371149190952905360 b=1513612962423956965
step 2:  a=1857536228528948395 b=1513612962423956965
step 3:  a=343923266104991430 b=1513612962423956965
step 4:  a=343923266104991430 b=1169689696318965535
step 5:  a=343923266104991430 b=825766430213974105
step 6:  a=343923266104991430 b=481843164108982675
step 7:  a=343923266104991430 b=137919898003991245
step 8:  a=206003368101000185 b=137919898003991245
step 9:  a=68083470097008940 b=137919898003991245
step 10:  a=68083470097008940 b=69836427906982305
step 11:  a=68083470097008940 b=1752957809973365
step 12:  a=66330512287035575 b=1752957809973365
step 13:  a=64577554477062210 b=1752957809973365
step 14:  a=62824596667088845 b=1752957809973365
step 15:  a=61071638857115480 b=1752957809973365
step 16:  a=59318681047142115 b=1752957809973365
step 17:  a=57565723237168750 b=1752957809973365
step 18:  a=55812765427195385 b=1752957809973365
step 19:  a=54059807617222020 b=1752957809973365
step 20:  a=52306849807248655 b=1752957809973365
step 21:  a=50553891997275290 b=1752957809973365
step 22:  a=48800934187301925 b=1752957809973365
step 23:  a=47047976377328560 b=1752957809973365
step 24:  a=45295018567355195 b=1752957809973365
step 25:  a=43542060757381830 b=1752957809973365
step 26:  a=41789102947408465 b=1752957809973365
step 27:  a=40036145137435100 b=1752957809973365
step 28:  a=38283187327461735 b=1752957809973365
step 29:  a=36530229517488370 b=1752957809973365
step 30:  a=34777271707515005 b=1752957809973365
step 31:  a=33024313897541640 b=1752957809973365
step 32:  a=31271356087568275 b=1752957809973365
step 33:  a=29518398277594910 b=1752957809973365
step 34:  a=27765440467621545 b=1752957809973365
step 35:  a=26012482657648180 b=1752957809973365
step 36:  a=24259524847674815 b=1752957809973365
step 37:  a=22506567037701450 b=1752957809973365
step 38:  a=20753609227728085 b=1752957809973365
step 39:  a=19000651417754720 b=1752957809973365
step 40:  a=17247693607781355 b=1752957809973365
step 41:  a=15494735797807990 b=1752957809973365
step 42:  a=13741777987834625 b=1752957809973365
step 43:  a=11988820177861260 b=1752957809973365
step 44:  a=10235862367887895 b=1752957809973365
step 45:  a=8482904557914530 b=1752957809973365
step 46:  a=6729946747941165 b=1752957809973365
step 47:  a=4976988937967800 b=1752957809973365
step 48:  a=3224031127994435 b=1752957809973365
step 49:  a=1471073318021070 b=1752957809973365
step 50:  a=1471073318021070 b=281884491952295
step 51:  a=1189188826068775 b=281884491952295
step 52:  a=907304334116480 b=281884491952295
step 53:  a=625419842164185 b=281884491952295
step 54:  a=343535350211890 b=281884491952295
step 55:  a=61650858259595 b=281884491952295
step 56:  a=61650858259595 b=220233633692700
step 57:  a=61650858259595 b=158582775433105
step 58:  a=61650858259595 b=96931917173510
step 59:  a=61650858259595 b=35281058913915
step 60:  a=26369799345680 b=35281058913915
step 61:  a=26369799345680 b=8911259568235
step 62:  a=17458539777445 b=8911259568235
step 63:  a=8547280209210 b=8911259568235
step 64:  a=8547280209210 b=363979359025
step 65:  a=8183300850185 b=363979359025
step 66:  a=7819321491160 b=363979359025
step 67:  a=7455342132135 b=363979359025
step 68:  a=7091362773110 b=363979359025
step 69:  a=6727383414085 b=363979359025
step 70:  a=6363404055060 b=363979359025
step 71:  a=5999424696035 b=363979359025
step 72:  a=5635445337010 b=363979359025
step 73:  a=5271465977985 b=363979359025
step 74:  a=4907486618960 b=363979359025
step 75:  a=4543507259935 b=363979359025
step 76:  a=4179527900910 b=363979359025
step 77:  a=3815548541885 b=363979359025
step 78:  a=3451569182860 b=363979359025
step 79:  a=3087589823835 b=363979359025
step 80:  a=2723610464810 b=363979359025
step 81:  a=2359631105785 b=363979359025
step 82:  a=1995651746760 b=363979359025
step 83:  a=1631672387735 b=363979359025
step 84:  a=1267693028710 b=363979359025
step 85:  a=903713669685 b=363979359025
step 86:  a=539734310660 b=363979359025
step 87:  a=175754951635 b=363979359025
step 88:  a=175754951635 b=188224407390
step 89:  a=175754951635 b=12469455755
step 90:  a=163285495880 b=12469455755
step 91:  a=150816040125 b=12469455755
step 92:  a=138346584370 b=12469455755
step 93:  a=125877128615 b=12469455755
step 94:  a=113407672860 b=12469455755
step 95:  a=100938217105 b=12469455755
step 96:  a=88468761350 b=12469455755
step 97:  a=75999305595 b=12469455755
step 98:  a=63529849840 b=12469455755
step 99:  a=51060394085 b=12469455755
step 100:  a=38590938330 b=12469455755
step 101:  a=26121482575 b=12469455755
step 102:  a=13652026820 b=12469455755
step 103:  a=1182571065 b=12469455755
step 104:  a=1182571065 b=11286884690
step 105:  a=1182571065 b=10104313625
step 106:  a=1182571065 b=8921742560
step 107:  a=1182571065 b=7739171495
step 108:  a=1182571065 b=6556600430
step 109:  a=1182571065 b=5374029365
step 110:  a=1182571065 b=4191458300
step 111:  a=1182571065 b=3008887235
step 112:  a=1182571065 b=1826316170
step 113:  a=1182571065 b=643745105
step 114:  a=538825960 b=643745105
step 115:  a=538825960 b=104919145
step 116:  a=433906815 b=104919145
step 117:  a=328987670 b=104919145
step 118:  a=224068525 b=104919145
step 119:  a=119149380 b=104919145
step 120:  a=14230235 b=104919145
step 121:  a=14230235 b=90688910
step 122:  a=14230235 b=76458675
step 123:  a=14230235 b=62228440
step 124:  a=14230235 b=47998205
step 125:  a=14230235 b=33767970
step 126:  a=14230235 b=19537735
step 127:  a=14230235 b=5307500
step 128:  a=8922735 b=5307500
step 129:  a=3615235 b=5307500
step 130:  a=3615235 b=1692265
step 131:  a=1922970 b=1692265
step 132:  a=230705 b=1692265
step 133:  a=230705 b=1461560
step 134:  a=230705 b=1230855
step 135:  a=230705 b=1000150
step 136:  a=230705 b=769445
step 137:  a=230705 b=538740
step 138:  a=230705 b=308035
step 139:  a=230705 b=77330
step 140:  a=153375 b=77330
step 141:  a=76045 b=77330
step 142:  a=76045 b=1285
step 143:  a=74760 b=1285
step 144:  a=73475 b=1285
step 145:  a=72190 b=1285
step 146:  a=70905 b=1285
step 147:  a=69620 b=1285
step 148:  a=68335 b=1285
step 149:  a=67050 b=1285
step 150:  a=65765 b=1285
step 151:  a=64480 b=1285
step 152:  a=63195 b=1285
step 153:  a=61910 b=1285
step 154:  a=60625 b=1285
step 155:  a=59340 b=1285
step 156:  a=58055 b=1285
step 157:  a=56770 b=1285
step 158:  a=55485 b=1285
step 159:  a=54200 b=1285
step 160:  a=52915 b=1285
step 161:  a=51630 b=1285
step 162:  a=50345 b=1285
step 163:  a=49060 b=1285
step 164:  a=47775 b=1285
step 165:  a=46490 b=1285
step 166:  a=45205 b=1285
step 167:  a=43920 b=1285
step 168:  a=42635 b=1285
step 169:  a=41350 b=1285
step 170:  a=40065 b=1285
step 171:  a=38780 b=1285
step 172:  a=37495 b=1285
step 173:  a=36210 b=1285
step 174:  a=34925 b=1285
step 175:  a=33640 b=1285
step 176:  a=32355 b=1285
step 177:  a=31070 b=1285
step 178:  a=29785 b=1285
step 179:  a=28500 b=1285
step 180:  a=27215 b=1285
step 181:  a=25930 b=1285
step 182:  a=24645 b=1285
step 183:  a=23360 b=1285
step 184:  a=22075 b=1285
step 185:  a=20790 b=1285
step 186:  a=19505 b=1285
step 187:  a=18220 b=1285
step 188:  a=16935 b=1285
step 189:  a=15650 b=1285
step 190:  a=14365 b=1285
step 191:  a=13080 b=1285
step 192:  a=11795 b=1285
step 193:  a=10510 b=1285
step 194:  a=9225 b=1285
step 195:  a=7940 b=1285
step 196:  a=6655 b=1285
step 197:  a=5370 b=1285
step 198:  a=4085 b=1285
step 199:  a=2800 b=1285
step 200:  a=1515 b=1285
step 201:  a=230 b=1285
step 202:  a=230 b=1055
step 203:  a=230 b=825
step 204:  a=230 b=595
step 205:  a=230 b=365
step 206:  a=230 b=135
step 207:  a=95 b=135
step 208:  a=95 b=40
step 209:  a=55 b=40
step 210:  a=15 b=40
step 211:  a=15 b=25
step 212:  a=15 b=10
step 213:  a=5 b=10
step 214:  a=5 b=5
5

This goes reasonably fast, but still requires a lot of steps... Instead of the difference, one can replace the smaller number by the remainder of Euclidean division of the larger number by the smaller one. In this way, our algorithm improves to:

function euclidlamegcd(a,b)
    i=0;
    while min(a,b)!=0
        if a > b
            a = a%b
        elseif a < b
            b = b%a
        end
    i+=1;
    println("step $(i):  a=$(a) b=$(b)")
    end
    max(a,b)
end

and indeed this is much "faster":

julia> euclidlamegcd(a,b)
step 1:  a=3371149190952905360 b=1513612962423956965
step 2:  a=343923266104991430 b=1513612962423956965
step 3:  a=343923266104991430 b=137919898003991245
step 4:  a=68083470097008940 b=137919898003991245
step 5:  a=68083470097008940 b=1752957809973365
step 6:  a=1471073318021070 b=1752957809973365
step 7:  a=1471073318021070 b=281884491952295
step 8:  a=61650858259595 b=281884491952295
step 9:  a=61650858259595 b=35281058913915
step 10:  a=26369799345680 b=35281058913915
step 11:  a=26369799345680 b=8911259568235
step 12:  a=8547280209210 b=8911259568235
step 13:  a=8547280209210 b=363979359025
step 14:  a=175754951635 b=363979359025
step 15:  a=175754951635 b=12469455755
step 16:  a=1182571065 b=12469455755
step 17:  a=1182571065 b=643745105
step 18:  a=538825960 b=643745105
step 19:  a=538825960 b=104919145
step 20:  a=14230235 b=104919145
step 21:  a=14230235 b=5307500
step 22:  a=3615235 b=5307500
step 23:  a=3615235 b=1692265
step 24:  a=230705 b=1692265
step 25:  a=230705 b=77330
step 26:  a=76045 b=77330
step 27:  a=76045 b=1285
step 28:  a=230 b=1285
step 29:  a=230 b=135
step 30:  a=95 b=135
step 31:  a=95 b=40
step 32:  a=15 b=40
step 33:  a=15 b=10
step 34:  a=5 b=10
step 35:  a=5 b=0
5

Check that the probability for two integers taken randomly have no common factor is given by $6/\pi^2$ [1].

This will check it numerically for a billion points:

julia> @time sum([euclidlamegcd(abs(rand(Int)),abs(rand(Int)))==1 for i=1:10^9])/10^9
427.323065 seconds (62.87 k allocations: 956.742 MiB, 0.04% gc time)
0.607932819
 
julia> 6/pi^2
0.6079271018540267

Here is the distribution:

julia> histogram([euclidlamegcd(abs(rand(Int)),abs(rand(Int))) for i=1:10^6],bins=1:20,yscale=:log10,
       legend=false,xlabel="gcd",norm=true,title="Probability of the gcd for two random integers")

The improvement from Euclid's method to the gcd makes the algorithm require a number of steps which is at most five times the number of digits (in base 10) of the smaller integer. This was proven by Gabriel Lamé in 1844 and marks the beginning of computational complexity theory.

Much of the rest of the course will in implementing such numerical algorithms, to tackle mathematical questions. In fact, the name "algorithm" itself comes from Muḥammad ibn Mūsā al-Khwārizmī, whom we already met in our Mathematics lectures when discussing algebra. We will see in particular how to find roots of nonlinear equations, differentiate and integrate, interpolate and extrapolate, solve differential equations, etc., but it would wrong to reduce algorithms and computer science to mathematical tasks of this type. In fact, we shall devote the next lecture to particular non-mathematical algorithms which Physicists should know about, because their tasks relate to physical concepts, or simply due to their importance.

Links

Table of Contents

Crash Course on Scientific Computing

@@ Line 232: / Line 232: @@
 <syntaxhighlight lang="python">
-julia> euclidgcd(abs(rand(Int)), abs(rand(Int)))
+julia> a=abs(rand(Int))
-step 1:  a=1695854002851361803 b=4884762153376862325
+3371149190952905360
-step 2:  a=1695854002851361803 b=3188908150525500522
-step 3:  a=1695854002851361803 b=1493054147674138719
+julia> b=4884762153376862325
-step 4:  a=202799855177223084 b=1493054147674138719
+4884762153376862325
-step 5:  a=202799855177223084 b=1290254292496915635
-step 6:  a=202799855177223084 b=1087454437319692551
+step 1:  a=3371149190952905360 b=1513612962423956965
-step 7:  a=202799855177223084 b=884654582142469467
+step 2:  a=1857536228528948395 b=1513612962423956965
-step 8:  a=202799855177223084 b=681854726965246383
+step 3:  a=343923266104991430 b=1513612962423956965
-step 9:  a=202799855177223084 b=479054871788023299
+step 4:  a=343923266104991430 b=1169689696318965535
-step 10:  a=202799855177223084 b=276255016610800215
+step 5:  a=343923266104991430 b=825766430213974105
-step 11:  a=202799855177223084 b=73455161433577131
+step 6:  a=343923266104991430 b=481843164108982675
-step 12:  a=129344693743645953 b=73455161433577131
+step 7:  a=343923266104991430 b=137919898003991245
-step 13:  a=55889532310068822 b=73455161433577131
+step 8:  a=206003368101000185 b=137919898003991245
-step 14:  a=55889532310068822 b=17565629123508309
+step 9:  a=68083470097008940 b=137919898003991245
-step 15:  a=38323903186560513 b=17565629123508309
+step 10:  a=68083470097008940 b=69836427906982305
-step 16:  a=20758274063052204 b=17565629123508309
+step 11:  a=68083470097008940 b=1752957809973365
-step 17:  a=3192644939543895 b=17565629123508309
+step 12:  a=66330512287035575 b=1752957809973365
-step 18:  a=3192644939543895 b=14372984183964414
+step 13:  a=64577554477062210 b=1752957809973365
-step 19:  a=3192644939543895 b=11180339244420519
+step 14:  a=62824596667088845 b=1752957809973365
-step 20:  a=3192644939543895 b=7987694304876624
+step 15:  a=61071638857115480 b=1752957809973365
-step 21:  a=3192644939543895 b=4795049365332729
+step 16:  a=59318681047142115 b=1752957809973365
-step 22:  a=3192644939543895 b=1602404425788834
+step 17:  a=57565723237168750 b=1752957809973365
-step 23:  a=1590240513755061 b=1602404425788834
+step 18:  a=55812765427195385 b=1752957809973365
-step 24:  a=1590240513755061 b=12163912033773
+step 19:  a=54059807617222020 b=1752957809973365
-step 25:  a=1578076601721288 b=12163912033773
+step 20:  a=52306849807248655 b=1752957809973365
-step 26:  a=1565912689687515 b=12163912033773
+step 21:  a=50553891997275290 b=1752957809973365
-step 27:  a=1553748777653742 b=12163912033773
+step 22:  a=48800934187301925 b=1752957809973365
-step 28:  a=1541584865619969 b=12163912033773
+step 23:  a=47047976377328560 b=1752957809973365
-step 29:  a=1529420953586196 b=12163912033773
+step 24:  a=45295018567355195 b=1752957809973365
-step 30:  a=1517257041552423 b=12163912033773
+step 25:  a=43542060757381830 b=1752957809973365
-step 31:  a=1505093129518650 b=12163912033773
+step 26:  a=41789102947408465 b=1752957809973365
-step 32:  a=1492929217484877 b=12163912033773
+step 27:  a=40036145137435100 b=1752957809973365
-step 33:  a=1480765305451104 b=12163912033773
+step 28:  a=38283187327461735 b=1752957809973365
-step 34:  a=1468601393417331 b=12163912033773
+step 29:  a=36530229517488370 b=1752957809973365
-step 35:  a=1456437481383558 b=12163912033773
+step 30:  a=34777271707515005 b=1752957809973365
-step 36:  a=1444273569349785 b=12163912033773
+step 31:  a=33024313897541640 b=1752957809973365
-step 37:  a=1432109657316012 b=12163912033773
+step 32:  a=31271356087568275 b=1752957809973365
-step 38:  a=1419945745282239 b=12163912033773
+step 33:  a=29518398277594910 b=1752957809973365
-step 39:  a=1407781833248466 b=12163912033773
+step 34:  a=27765440467621545 b=1752957809973365
-step 40:  a=1395617921214693 b=12163912033773
+step 35:  a=26012482657648180 b=1752957809973365
-step 41:  a=1383454009180920 b=12163912033773
+step 36:  a=24259524847674815 b=1752957809973365
-step 42:  a=1371290097147147 b=12163912033773
+step 37:  a=22506567037701450 b=1752957809973365
-step 43:  a=1359126185113374 b=12163912033773
+step 38:  a=20753609227728085 b=1752957809973365
-step 44:  a=1346962273079601 b=12163912033773
+step 39:  a=19000651417754720 b=1752957809973365
-step 45:  a=1334798361045828 b=12163912033773
+step 40:  a=17247693607781355 b=1752957809973365
-step 46:  a=1322634449012055 b=12163912033773
+step 41:  a=15494735797807990 b=1752957809973365
-step 47:  a=1310470536978282 b=12163912033773
+step 42:  a=13741777987834625 b=1752957809973365
-step 48:  a=1298306624944509 b=12163912033773
+step 43:  a=11988820177861260 b=1752957809973365
-step 49:  a=1286142712910736 b=12163912033773
+step 44:  a=10235862367887895 b=1752957809973365
-step 50:  a=1273978800876963 b=12163912033773
+step 45:  a=8482904557914530 b=1752957809973365
-step 51:  a=1261814888843190 b=12163912033773
+step 46:  a=6729946747941165 b=1752957809973365
-step 52:  a=1249650976809417 b=12163912033773
+step 47:  a=4976988937967800 b=1752957809973365
-step 53:  a=1237487064775644 b=12163912033773
+step 48:  a=3224031127994435 b=1752957809973365
-step 54:  a=1225323152741871 b=12163912033773
+step 49:  a=1471073318021070 b=1752957809973365
-step 55:  a=1213159240708098 b=12163912033773
+step 50:  a=1471073318021070 b=281884491952295
-step 56:  a=1200995328674325 b=12163912033773
+step 51:  a=1189188826068775 b=281884491952295
-step 57:  a=1188831416640552 b=12163912033773
+step 52:  a=907304334116480 b=281884491952295
-step 58:  a=1176667504606779 b=12163912033773
+step 53:  a=625419842164185 b=281884491952295
-step 59:  a=1164503592573006 b=12163912033773
+step 54:  a=343535350211890 b=281884491952295
-step 60:  a=1152339680539233 b=12163912033773
+step 55:  a=61650858259595 b=281884491952295
-step 61:  a=1140175768505460 b=12163912033773
+step 56:  a=61650858259595 b=220233633692700
-step 62:  a=1128011856471687 b=12163912033773
+step 57:  a=61650858259595 b=158582775433105
-step 63:  a=1115847944437914 b=12163912033773
+step 58:  a=61650858259595 b=96931917173510
-step 64:  a=1103684032404141 b=12163912033773
+step 59:  a=61650858259595 b=35281058913915
-step 65:  a=1091520120370368 b=12163912033773
+step 60:  a=26369799345680 b=35281058913915
-step 66:  a=1079356208336595 b=12163912033773
+step 61:  a=26369799345680 b=8911259568235
-step 67:  a=1067192296302822 b=12163912033773
+step 62:  a=17458539777445 b=8911259568235
-step 68:  a=1055028384269049 b=12163912033773
+step 63:  a=8547280209210 b=8911259568235
-step 69:  a=1042864472235276 b=12163912033773
+step 64:  a=8547280209210 b=363979359025
-step 70:  a=1030700560201503 b=12163912033773
+step 65:  a=8183300850185 b=363979359025
-step 71:  a=1018536648167730 b=12163912033773
+step 66:  a=7819321491160 b=363979359025
-step 72:  a=1006372736133957 b=12163912033773
+step 67:  a=7455342132135 b=363979359025
-step 73:  a=994208824100184 b=12163912033773
+step 68:  a=7091362773110 b=363979359025
-step 74:  a=982044912066411 b=12163912033773
+step 69:  a=6727383414085 b=363979359025
-step 75:  a=969881000032638 b=12163912033773
+step 70:  a=6363404055060 b=363979359025
-step 76:  a=957717087998865 b=12163912033773
+step 71:  a=5999424696035 b=363979359025
-step 77:  a=945553175965092 b=12163912033773
+step 72:  a=5635445337010 b=363979359025
-step 78:  a=933389263931319 b=12163912033773
+step 73:  a=5271465977985 b=363979359025
-step 79:  a=921225351897546 b=12163912033773
+step 74:  a=4907486618960 b=363979359025
-step 80:  a=909061439863773 b=12163912033773
+step 75:  a=4543507259935 b=363979359025
-step 81:  a=896897527830000 b=12163912033773
+step 76:  a=4179527900910 b=363979359025
-step 82:  a=884733615796227 b=12163912033773
+step 77:  a=3815548541885 b=363979359025
-step 83:  a=872569703762454 b=12163912033773
+step 78:  a=3451569182860 b=363979359025
-step 84:  a=860405791728681 b=12163912033773
+step 79:  a=3087589823835 b=363979359025
-step 85:  a=848241879694908 b=12163912033773
+step 80:  a=2723610464810 b=363979359025
-step 86:  a=836077967661135 b=12163912033773
+step 81:  a=2359631105785 b=363979359025
-step 87:  a=823914055627362 b=12163912033773
+step 82:  a=1995651746760 b=363979359025
-step 88:  a=811750143593589 b=12163912033773
+step 83:  a=1631672387735 b=363979359025
-step 89:  a=799586231559816 b=12163912033773
+step 84:  a=1267693028710 b=363979359025
-step 90:  a=787422319526043 b=12163912033773
+step 85:  a=903713669685 b=363979359025
-step 91:  a=775258407492270 b=12163912033773
+step 86:  a=539734310660 b=363979359025
-step 92:  a=763094495458497 b=12163912033773
+step 87:  a=175754951635 b=363979359025
-step 93:  a=750930583424724 b=12163912033773
+step 88:  a=175754951635 b=188224407390
-step 94:  a=738766671390951 b=12163912033773
+step 89:  a=175754951635 b=12469455755
-step 95:  a=726602759357178 b=12163912033773
+step 90:  a=163285495880 b=12469455755
-step 96:  a=714438847323405 b=12163912033773
+step 91:  a=150816040125 b=12469455755
-step 97:  a=702274935289632 b=12163912033773
+step 92:  a=138346584370 b=12469455755
-step 98:  a=690111023255859 b=12163912033773
+step 93:  a=125877128615 b=12469455755
-step 99:  a=677947111222086 b=12163912033773
+step 94:  a=113407672860 b=12469455755
-step 100:  a=665783199188313 b=12163912033773
+step 95:  a=100938217105 b=12469455755
-step 101:  a=653619287154540 b=12163912033773
+step 96:  a=88468761350 b=12469455755
-step 102:  a=641455375120767 b=12163912033773
+step 97:  a=75999305595 b=12469455755
-step 103:  a=629291463086994 b=12163912033773
+step 98:  a=63529849840 b=12469455755
-step 104:  a=617127551053221 b=12163912033773
+step 99:  a=51060394085 b=12469455755
-step 105:  a=604963639019448 b=12163912033773
+step 100:  a=38590938330 b=12469455755
-step 106:  a=592799726985675 b=12163912033773
+step 101:  a=26121482575 b=12469455755
-step 107:  a=580635814951902 b=12163912033773
+step 102:  a=13652026820 b=12469455755
-step 108:  a=568471902918129 b=12163912033773
+step 103:  a=1182571065 b=12469455755
-step 109:  a=556307990884356 b=12163912033773
+step 104:  a=1182571065 b=11286884690
-step 110:  a=544144078850583 b=12163912033773
+step 105:  a=1182571065 b=10104313625
-step 111:  a=531980166816810 b=12163912033773
+step 106:  a=1182571065 b=8921742560
-step 112:  a=519816254783037 b=12163912033773
+step 107:  a=1182571065 b=7739171495
-step 113:  a=507652342749264 b=12163912033773
+step 108:  a=1182571065 b=6556600430
-step 114:  a=495488430715491 b=12163912033773
+step 109:  a=1182571065 b=5374029365
-step 115:  a=483324518681718 b=12163912033773
+step 110:  a=1182571065 b=4191458300
-step 116:  a=471160606647945 b=12163912033773
+step 111:  a=1182571065 b=3008887235
-step 117:  a=458996694614172 b=12163912033773
+step 112:  a=1182571065 b=1826316170
-step 118:  a=446832782580399 b=12163912033773
+step 113:  a=1182571065 b=643745105
-step 119:  a=434668870546626 b=12163912033773
+step 114:  a=538825960 b=643745105
-step 120:  a=422504958512853 b=12163912033773
+step 115:  a=538825960 b=104919145
-step 121:  a=410341046479080 b=12163912033773
+step 116:  a=433906815 b=104919145
-step 122:  a=398177134445307 b=12163912033773
+step 117:  a=328987670 b=104919145
-step 123:  a=386013222411534 b=12163912033773
+step 118:  a=224068525 b=104919145
-step 124:  a=373849310377761 b=12163912033773
+step 119:  a=119149380 b=104919145
-step 125:  a=361685398343988 b=12163912033773
+step 120:  a=14230235 b=104919145
-step 126:  a=349521486310215 b=12163912033773
+step 121:  a=14230235 b=90688910
-step 127:  a=337357574276442 b=12163912033773
+step 122:  a=14230235 b=76458675
-step 128:  a=325193662242669 b=12163912033773
+step 123:  a=14230235 b=62228440
-step 129:  a=313029750208896 b=12163912033773
+step 124:  a=14230235 b=47998205
-step 130:  a=300865838175123 b=12163912033773
+step 125:  a=14230235 b=33767970
-step 131:  a=288701926141350 b=12163912033773
+step 126:  a=14230235 b=19537735
-step 132:  a=276538014107577 b=12163912033773
+step 127:  a=14230235 b=5307500
-step 133:  a=264374102073804 b=12163912033773
+step 128:  a=8922735 b=5307500
-step 134:  a=252210190040031 b=12163912033773
+step 129:  a=3615235 b=5307500
-step 135:  a=240046278006258 b=12163912033773
+step 130:  a=3615235 b=1692265
-step 136:  a=227882365972485 b=12163912033773
+step 131:  a=1922970 b=1692265
-step 137:  a=215718453938712 b=12163912033773
+step 132:  a=230705 b=1692265
-step 138:  a=203554541904939 b=12163912033773
+step 133:  a=230705 b=1461560
-step 139:  a=191390629871166 b=12163912033773
+step 134:  a=230705 b=1230855
-step 140:  a=179226717837393 b=12163912033773
+step 135:  a=230705 b=1000150
-step 141:  a=167062805803620 b=12163912033773
+step 136:  a=230705 b=769445
-step 142:  a=154898893769847 b=12163912033773
+step 137:  a=230705 b=538740
-step 143:  a=142734981736074 b=12163912033773
+step 138:  a=230705 b=308035
-step 144:  a=130571069702301 b=12163912033773
+step 139:  a=230705 b=77330
-step 145:  a=118407157668528 b=12163912033773
+step 140:  a=153375 b=77330
-step 146:  a=106243245634755 b=12163912033773
+step 141:  a=76045 b=77330
-step 147:  a=94079333600982 b=12163912033773
+step 142:  a=76045 b=1285
-step 148:  a=81915421567209 b=12163912033773
+step 143:  a=74760 b=1285
-step 149:  a=69751509533436 b=12163912033773
+step 144:  a=73475 b=1285
-step 150:  a=57587597499663 b=12163912033773
+step 145:  a=72190 b=1285
-step 151:  a=45423685465890 b=12163912033773
+step 146:  a=70905 b=1285
-step 152:  a=33259773432117 b=12163912033773
+step 147:  a=69620 b=1285
-step 153:  a=21095861398344 b=12163912033773
+step 148:  a=68335 b=1285
-step 154:  a=8931949364571 b=12163912033773
+step 149:  a=67050 b=1285
-step 155:  a=8931949364571 b=3231962669202
+step 150:  a=65765 b=1285
-step 156:  a=5699986695369 b=3231962669202
+step 151:  a=64480 b=1285
-step 157:  a=2468024026167 b=3231962669202
+step 152:  a=63195 b=1285
-step 158:  a=2468024026167 b=763938643035
+step 153:  a=61910 b=1285
-step 159:  a=1704085383132 b=763938643035
+step 154:  a=60625 b=1285
-step 160:  a=940146740097 b=763938643035
+step 155:  a=59340 b=1285
-step 161:  a=176208097062 b=763938643035
+step 156:  a=58055 b=1285
-step 162:  a=176208097062 b=587730545973
+step 157:  a=56770 b=1285
-step 163:  a=176208097062 b=411522448911
+step 158:  a=55485 b=1285
-step 164:  a=176208097062 b=235314351849
+step 159:  a=54200 b=1285
-step 165:  a=176208097062 b=59106254787
+step 160:  a=52915 b=1285
-step 166:  a=117101842275 b=59106254787
+step 161:  a=51630 b=1285
-step 167:  a=57995587488 b=59106254787
+step 162:  a=50345 b=1285
-step 168:  a=57995587488 b=1110667299
+step 163:  a=49060 b=1285
-step 169:  a=56884920189 b=1110667299
+step 164:  a=47775 b=1285
-step 170:  a=55774252890 b=1110667299
+step 165:  a=46490 b=1285
-step 171:  a=54663585591 b=1110667299
+step 166:  a=45205 b=1285
-step 172:  a=53552918292 b=1110667299
+step 167:  a=43920 b=1285
-step 173:  a=52442250993 b=1110667299
+step 168:  a=42635 b=1285
-step 174:  a=51331583694 b=1110667299
+step 169:  a=41350 b=1285
-step 175:  a=50220916395 b=1110667299
+step 170:  a=40065 b=1285
-step 176:  a=49110249096 b=1110667299
+step 171:  a=38780 b=1285
-step 177:  a=47999581797 b=1110667299
+step 172:  a=37495 b=1285
-step 178:  a=46888914498 b=1110667299
+step 173:  a=36210 b=1285
-step 179:  a=45778247199 b=1110667299
+step 174:  a=34925 b=1285
-step 180:  a=44667579900 b=1110667299
+step 175:  a=33640 b=1285
-step 181:  a=43556912601 b=1110667299
+step 176:  a=32355 b=1285
-step 182:  a=42446245302 b=1110667299
+step 177:  a=31070 b=1285
-step 183:  a=41335578003 b=1110667299
+step 178:  a=29785 b=1285
-step 184:  a=40224910704 b=1110667299
+step 179:  a=28500 b=1285
-step 185:  a=39114243405 b=1110667299
+step 180:  a=27215 b=1285
-step 186:  a=38003576106 b=1110667299
+step 181:  a=25930 b=1285
-step 187:  a=36892908807 b=1110667299
+step 182:  a=24645 b=1285
-step 188:  a=35782241508 b=1110667299
+step 183:  a=23360 b=1285
-step 189:  a=34671574209 b=1110667299
+step 184:  a=22075 b=1285
-step 190:  a=33560906910 b=1110667299
+step 185:  a=20790 b=1285
-step 191:  a=32450239611 b=1110667299
+step 186:  a=19505 b=1285
-step 192:  a=31339572312 b=1110667299
+step 187:  a=18220 b=1285
-step 193:  a=30228905013 b=1110667299
+step 188:  a=16935 b=1285
-step 194:  a=29118237714 b=1110667299
+step 189:  a=15650 b=1285
-step 195:  a=28007570415 b=1110667299
+step 190:  a=14365 b=1285
-step 196:  a=26896903116 b=1110667299
+step 191:  a=13080 b=1285
-step 197:  a=25786235817 b=1110667299
+step 192:  a=11795 b=1285
-step 198:  a=24675568518 b=1110667299
+step 193:  a=10510 b=1285
-step 199:  a=23564901219 b=1110667299
+step 194:  a=9225 b=1285
-step 200:  a=22454233920 b=1110667299
+step 195:  a=7940 b=1285
-step 201:  a=21343566621 b=1110667299
+step 196:  a=6655 b=1285
-step 202:  a=20232899322 b=1110667299
+step 197:  a=5370 b=1285
-step 203:  a=19122232023 b=1110667299
+step 198:  a=4085 b=1285
-step 204:  a=18011564724 b=1110667299
+step 199:  a=2800 b=1285
-step 205:  a=16900897425 b=1110667299
+step 200:  a=1515 b=1285
-step 206:  a=15790230126 b=1110667299
+step 201:  a=230 b=1285
-step 207:  a=14679562827 b=1110667299
+step 202:  a=230 b=1055
-step 208:  a=13568895528 b=1110667299
+step 203:  a=230 b=825
-step 209:  a=12458228229 b=1110667299
+step 204:  a=230 b=595
-step 210:  a=11347560930 b=1110667299
+step 205:  a=230 b=365
-step 211:  a=10236893631 b=1110667299
+step 206:  a=230 b=135
-step 212:  a=9126226332 b=1110667299
+step 207:  a=95 b=135
-step 213:  a=8015559033 b=1110667299
+step 208:  a=95 b=40
-step 214:  a=6904891734 b=1110667299
+step 209:  a=55 b=40
-step 215:  a=5794224435 b=1110667299
+step 210:  a=15 b=40
-step 216:  a=4683557136 b=1110667299
+step 211:  a=15 b=25
-step 217:  a=3572889837 b=1110667299
+step 212:  a=15 b=10
-step 218:  a=2462222538 b=1110667299
+step 213:  a=5 b=10
-step 219:  a=1351555239 b=1110667299
+step 214:  a=5 b=5
-step 220:  a=240887940 b=1110667299
-step 221:  a=240887940 b=869779359
-step 222:  a=240887940 b=628891419
-step 223:  a=240887940 b=388003479
-step 224:  a=240887940 b=147115539
-step 225:  a=93772401 b=147115539
-step 226:  a=93772401 b=53343138
-step 227:  a=40429263 b=53343138
-step 228:  a=40429263 b=12913875
-step 229:  a=27515388 b=12913875
-step 230:  a=14601513 b=12913875
-step 231:  a=1687638 b=12913875
-step 232:  a=1687638 b=11226237
-step 233:  a=1687638 b=9538599
-step 234:  a=1687638 b=7850961
-step 235:  a=1687638 b=6163323
-step 236:  a=1687638 b=4475685
-step 237:  a=1687638 b=2788047
-step 238:  a=1687638 b=1100409
-step 239:  a=587229 b=1100409
-step 240:  a=587229 b=513180
-step 241:  a=74049 b=513180
-step 242:  a=74049 b=439131
-step 243:  a=74049 b=365082
-step 244:  a=74049 b=291033
-step 245:  a=74049 b=216984
-step 246:  a=74049 b=142935
-step 247:  a=74049 b=68886
-step 248:  a=5163 b=68886
-step 249:  a=5163 b=63723
-step 250:  a=5163 b=58560
-step 251:  a=5163 b=53397
-step 252:  a=5163 b=48234
-step 253:  a=5163 b=43071
-step 254:  a=5163 b=37908
-step 255:  a=5163 b=32745
-step 256:  a=5163 b=27582
-step 257:  a=5163 b=22419
-step 258:  a=5163 b=17256
-step 259:  a=5163 b=12093
-step 260:  a=5163 b=6930
-step 261:  a=5163 b=1767
-step 262:  a=3396 b=1767
-step 263:  a=1629 b=1767
-step 264:  a=1629 b=138
-step 265:  a=1491 b=138
-step 266:  a=1353 b=138
-step 267:  a=1215 b=138
-step 268:  a=1077 b=138
-step 269:  a=939 b=138
-step 270:  a=801 b=138
-step 271:  a=663 b=138
-step 272:  a=525 b=138
-step 273:  a=387 b=138
-step 274:  a=249 b=138
-step 275:  a=111 b=138
-step 276:  a=111 b=27
-step 277:  a=84 b=27
-step 278:  a=57 b=27
-step 279:  a=30 b=27
-step 280:  a=3 b=27
-step 281:  a=3 b=24
-step 282:  a=3 b=21
-step 283:  a=3 b=18
-step 284:  a=3 b=15
-step 285:  a=3 b=12
-step 286:  a=3 b=9
-step 287:  a=3 b=6
-step 288:  a=3 b=3
 </syntaxhighlight>
@@ Line 538: / Line 469: @@
      println("step $(i):  a=$(a) b=$(b)")
      end
-     a
+     max(a,b)
 end
 </syntaxhighlight>
 and indeed this is much "faster":
+<syntaxhighlight lang="python">
+julia> euclidlamegcd(a,b)
+step 1:  a=3371149190952905360 b=1513612962423956965
+step 2:  a=343923266104991430 b=1513612962423956965
+step 3:  a=343923266104991430 b=137919898003991245
+step 4:  a=68083470097008940 b=137919898003991245
+step 5:  a=68083470097008940 b=1752957809973365
+step 6:  a=1471073318021070 b=1752957809973365
+step 7:  a=1471073318021070 b=281884491952295
+step 8:  a=61650858259595 b=281884491952295
+step 9:  a=61650858259595 b=35281058913915
+step 10:  a=26369799345680 b=35281058913915
+step 11:  a=26369799345680 b=8911259568235
+step 12:  a=8547280209210 b=8911259568235
+step 13:  a=8547280209210 b=363979359025
+step 14:  a=175754951635 b=363979359025
+step 15:  a=175754951635 b=12469455755
+step 16:  a=1182571065 b=12469455755
+step 17:  a=1182571065 b=643745105
+step 18:  a=538825960 b=643745105
+step 19:  a=538825960 b=104919145
+step 20:  a=14230235 b=104919145
+step 21:  a=14230235 b=5307500
+step 22:  a=3615235 b=5307500
+step 23:  a=3615235 b=1692265
+step 24:  a=230705 b=1692265
+step 25:  a=230705 b=77330
+step 26:  a=76045 b=77330
+step 27:  a=76045 b=1285
+step 28:  a=230 b=1285
+step 29:  a=230 b=135
+step 30:  a=95 b=135
+step 31:  a=95 b=40
+step 32:  a=15 b=40
+step 33:  a=15 b=10
+step 34:  a=5 b=10
+step 35:  a=5 b=0
+</syntaxhighlight>
+{{exstart}}
+Check that the probability for two integers taken randomly have no common factor is given by $6/\pi^2$ [https://twitter.com/fermatslibrary/status/1364949783748706312].
+{{anstart}}
+This will check it numerically for a billion points:
+<syntaxhighlight lang="python">
+julia> @time sum([euclidlamegcd(abs(rand(Int)),abs(rand(Int)))==1 for i=1:10^9])/10^9
+.323065 seconds (62.87 k allocations: 956.742 MiB, 0.04% gc time)
+.607932819
+julia> 6/pi^2
+.6079271018540267
+</syntaxhighlight>
+Here is the distribution:
+<syntaxhighlight lang="python">
+julia> histogram([euclidlamegcd(abs(rand(Int)),abs(rand(Int))) for i=1:10^6],bins=1:20,yscale=:log10,
+       legend=false,xlabel="gcd",norm=true,title="Probability of the gcd for two random integers")
+</syntaxhighlight>
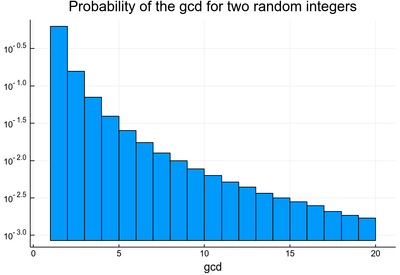
+<center><wz tip="Numerically computed probabilities that two randomly sampled integers will be found with a given gcd (up to 19)">[[File:Screenshot_20210301_172603.png|400px]]</wz></center>
+{{anstop}}
+{{exstop}}
+The improvement from Euclid's method to the gcd makes the algorithm require a number of steps which is at most five times the number of digits (in base 10) of the smaller integer. This was proven by Gabriel Lamé in 1844 and marks the beginning of computational complexity theory.
 Much of the rest of the course will in implementing such numerical algorithms, to tackle mathematical questions. In fact, the name "algorithm" itself comes from Muḥammad ibn Mūsā al-Khwārizmī, whom we already met in our [[Mathematics]] lectures when discussing algebra. We will see in particular how to find roots of nonlinear equations, differentiate and integrate, interpolate and extrapolate, solve differential equations, etc., but it would wrong to reduce algorithms and computer science to mathematical tasks of this type. In fact, we shall devote the next lecture to particular non-mathematical algorithms which Physicists should know about, because their tasks relate to physical concepts, or simply due to their importance.