m |
m |
||
| Line 82: | Line 82: | ||
0.0027113203900000003 | 0.0027113203900000003 | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| + | |||
| + | The "complexity" of our find-max algorithm is linear: it grows in direct proportion to the size of the input, as can be understood easily from the way the algorithm is designed. Here is this relationship explictely calculated by the computer: | ||
| + | |||
| + | <syntaxhighlight lang="python"> | ||
| + | julia> lt=[@elapsed myfindmax(rand(10^i)) for i=1:8] | ||
| + | julia> scatter(lt, yscale=:log10, xlabel="10^n numbers", ylabel="Time (s)", | ||
| + | title="Finding maximum in a list", legend=false) | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | <center><wz tip="Linear increase of the time needed to sort random numbers, up to 100 millions (the latter taking 0.38s).">[[File:Screenshot_20210301_114523.png|400px]]</wz></center> | ||
To do even more advanced benchmarking, one can be | To do even more advanced benchmarking, one can be | ||
| Line 119: | Line 129: | ||
The fact that our readily-made version is faster than the one provided by the system has been flagged by the Julia community and has been traced to [https://github.com/JuliaLang/julia/issues/26003 time being lost when checking for NaN numbers]. | The fact that our readily-made version is faster than the one provided by the system has been flagged by the Julia community and has been traced to [https://github.com/JuliaLang/julia/issues/26003 time being lost when checking for NaN numbers]. | ||
| − | + | Algorithms usually rely on tricks or clever observations. For instance, whatever the numbers $y$ and $x$, it is always true that $\sqrt{x}$ is comprised between $y$ and $x/y$. This is easy to prove and follow from the fact that $1/\sqrt{x}=\sqrt{x}/x$. If $y<\sqrt{x}$, then $1/y>\sqrt{x}/x$ which brings us to | |
| + | $$y<\sqrt{x}<x/y$$ | ||
| − | + | while if $y>\sqrt{x}$ then, similarly, $1/y<\sqrt{x}/x$ and we have the opposite inequality | |
| − | + | $$x/y<\sqrt{x}<y$$ | |
| − | + | So given to numbers $x$ and $y$, a good guess to approximate $\sqrt{x}$ is to take their average ${1\over2}(y+x/y)$. We now have a number closer to $\sqrt{x}$, so we can simply iterate. This is, thus, our algorithm, start with any $y_0\neq x$ and compute: | |
| + | |||
| + | $$y_{n+1}={1\over2}\left(y_n+{x\over y_n}\right)$$ | ||
| + | |||
| + | This will converge to $\sqrt{x}$. This method was known to the Babylonians to compute $\sqrt{2}$. This is the Julia code: | ||
| + | |||
| + | <syntaxhighlight lang="python"> | ||
| + | julia> x=2; y=1; | ||
| + | julia> while abs(y^2-x)>10^-12 | ||
| + | global y=(1/2)*(y+x/y) | ||
| + | println(y) | ||
| + | end | ||
| + | 1.5 | ||
| + | 1.4166666666666665 | ||
| + | 1.4142156862745097 | ||
| + | 1.4142135623746899 | ||
| + | 1.414213562373095 | ||
| + | |||
| + | julia> √2 | ||
| + | 1.4142135623730951 | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | This is frustratingly fast! Numerical analysis shows that the number of significant digits doubles at each step. We don't need any better algorithm than this one designed by the Babylonians, and this is actually the steps that are undertaken by your pocket calculator, or any computer for that matter, when you press the √ button. Wherever it starts from, in just a few steps, it will have all the decimals of its accuracy correct to the sought square root. So now you how this happens. Let us see other implementations of important operations. | ||
Sieve of Eratosthenes | Sieve of Eratosthenes | ||
| − | + | {{exstart}} | |
| + | Find the largest prime below 1,000,000,000 | ||
| + | <div class="toccolours mw-collapsible" style="width:400px; overflow:auto;"> | ||
| + | Answer: This is 999,999,937 | ||
| + | </div> | ||
| + | {{exstop}} | ||
| + | Division algorithm/Euclidean algorithm | ||
| + | Euclidean—or integer—division takes two (positive, without loss of generality) integers $a$ (numerator) and $b$ (denominator) and returns another two integers: $q$ (quotient) and $r$ (remainder) | ||
| + | |||
| + | $$a=bq+r$$ | ||
| + | |||
| + | with $0\ge q<p$. We have seen that julia computes these quantities directly so there is no need of an algorithm per se: | ||
| + | |||
| + | <syntaxhighlight lang="python"> | ||
| + | julia> function juliadiv(a,b) | ||
| + | [a÷b, a%b] | ||
| + | end | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | but to illustrate the point, let us look at various implementations. The oldest one is from Euclid himself, in his [https://en.wikipedia.org/wiki/Euclid%27s_Elements Elements], Book VII, Proposition 1, a simple method is proposed: starting with $r=a$, while $r\ge b$, subtract $b$ from $r$ and take this as the new $r$ and when this is not possible, what is left is the final remainder $r$. The number of times it took to get there is $q$. In julia code: | ||
| + | |||
| + | <syntaxhighlight lang="python"> | ||
| + | function eucliddiv(a,b) | ||
| + | r=a | ||
| + | q=0 | ||
| + | while r-b ≥ 0 | ||
| + | q+=1 | ||
| + | r=r-b | ||
| + | end | ||
| + | [q r] | ||
| + | end | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | This is very simple but can get quite lengthy. One would use long division algorithms for faster results. Instead of looking at those now, we turn to an important historical algorithm, Euclid's algorithm, which computes the gcd (greatest common divisor between two numbers). This is one of the oldest known algorithms. It is based one the fact that the gcd of two numbers is the same as the gcd of the smaller number with the positive difference of the numbers, so that by iterations, one can decrease the values of the numbers until they become equal, at which point the value thus found is the gcd. This is a julia implementation: | ||
| + | |||
| + | <syntaxhighlight lang="python"> | ||
| + | function euclidgcd(a,b) | ||
| + | while a!=b | ||
| + | if a > b | ||
| + | a = a-b | ||
| + | elseif a < b | ||
| + | b = b-a | ||
| + | end | ||
| + | end | ||
| + | a | ||
| + | end | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | This is the result, showing the details of the intermediate steps: | ||
| + | |||
| + | <syntaxhighlight lang="python"> | ||
| + | function euclidgcd(a,b) | ||
| + | i=0; | ||
| + | while a!=b | ||
| + | if a > b | ||
| + | a = a-b | ||
| + | elseif a < b | ||
| + | b = b-a | ||
| + | end | ||
| + | i+=1; | ||
| + | println("step $(i): a=$(a) b=$(b)") | ||
| + | end | ||
| + | a | ||
| + | end | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | <syntaxhighlight lang="python"> | ||
| + | julia> euclidgcd(abs(rand(Int)), abs(rand(Int))) | ||
| + | step 1: a=1695854002851361803 b=4884762153376862325 | ||
| + | step 2: a=1695854002851361803 b=3188908150525500522 | ||
| + | step 3: a=1695854002851361803 b=1493054147674138719 | ||
| + | step 4: a=202799855177223084 b=1493054147674138719 | ||
| + | step 5: a=202799855177223084 b=1290254292496915635 | ||
| + | step 6: a=202799855177223084 b=1087454437319692551 | ||
| + | step 7: a=202799855177223084 b=884654582142469467 | ||
| + | step 8: a=202799855177223084 b=681854726965246383 | ||
| + | step 9: a=202799855177223084 b=479054871788023299 | ||
| + | step 10: a=202799855177223084 b=276255016610800215 | ||
| + | step 11: a=202799855177223084 b=73455161433577131 | ||
| + | step 12: a=129344693743645953 b=73455161433577131 | ||
| + | step 13: a=55889532310068822 b=73455161433577131 | ||
| + | step 14: a=55889532310068822 b=17565629123508309 | ||
| + | step 15: a=38323903186560513 b=17565629123508309 | ||
| + | step 16: a=20758274063052204 b=17565629123508309 | ||
| + | step 17: a=3192644939543895 b=17565629123508309 | ||
| + | step 18: a=3192644939543895 b=14372984183964414 | ||
| + | step 19: a=3192644939543895 b=11180339244420519 | ||
| + | step 20: a=3192644939543895 b=7987694304876624 | ||
| + | step 21: a=3192644939543895 b=4795049365332729 | ||
| + | step 22: a=3192644939543895 b=1602404425788834 | ||
| + | step 23: a=1590240513755061 b=1602404425788834 | ||
| + | step 24: a=1590240513755061 b=12163912033773 | ||
| + | step 25: a=1578076601721288 b=12163912033773 | ||
| + | step 26: a=1565912689687515 b=12163912033773 | ||
| + | step 27: a=1553748777653742 b=12163912033773 | ||
| + | step 28: a=1541584865619969 b=12163912033773 | ||
| + | step 29: a=1529420953586196 b=12163912033773 | ||
| + | step 30: a=1517257041552423 b=12163912033773 | ||
| + | step 31: a=1505093129518650 b=12163912033773 | ||
| + | step 32: a=1492929217484877 b=12163912033773 | ||
| + | step 33: a=1480765305451104 b=12163912033773 | ||
| + | step 34: a=1468601393417331 b=12163912033773 | ||
| + | step 35: a=1456437481383558 b=12163912033773 | ||
| + | step 36: a=1444273569349785 b=12163912033773 | ||
| + | step 37: a=1432109657316012 b=12163912033773 | ||
| + | step 38: a=1419945745282239 b=12163912033773 | ||
| + | step 39: a=1407781833248466 b=12163912033773 | ||
| + | step 40: a=1395617921214693 b=12163912033773 | ||
| + | step 41: a=1383454009180920 b=12163912033773 | ||
| + | step 42: a=1371290097147147 b=12163912033773 | ||
| + | step 43: a=1359126185113374 b=12163912033773 | ||
| + | step 44: a=1346962273079601 b=12163912033773 | ||
| + | step 45: a=1334798361045828 b=12163912033773 | ||
| + | step 46: a=1322634449012055 b=12163912033773 | ||
| + | step 47: a=1310470536978282 b=12163912033773 | ||
| + | step 48: a=1298306624944509 b=12163912033773 | ||
| + | step 49: a=1286142712910736 b=12163912033773 | ||
| + | step 50: a=1273978800876963 b=12163912033773 | ||
| + | step 51: a=1261814888843190 b=12163912033773 | ||
| + | step 52: a=1249650976809417 b=12163912033773 | ||
| + | step 53: a=1237487064775644 b=12163912033773 | ||
| + | step 54: a=1225323152741871 b=12163912033773 | ||
| + | step 55: a=1213159240708098 b=12163912033773 | ||
| + | step 56: a=1200995328674325 b=12163912033773 | ||
| + | step 57: a=1188831416640552 b=12163912033773 | ||
| + | step 58: a=1176667504606779 b=12163912033773 | ||
| + | step 59: a=1164503592573006 b=12163912033773 | ||
| + | step 60: a=1152339680539233 b=12163912033773 | ||
| + | step 61: a=1140175768505460 b=12163912033773 | ||
| + | step 62: a=1128011856471687 b=12163912033773 | ||
| + | step 63: a=1115847944437914 b=12163912033773 | ||
| + | step 64: a=1103684032404141 b=12163912033773 | ||
| + | step 65: a=1091520120370368 b=12163912033773 | ||
| + | step 66: a=1079356208336595 b=12163912033773 | ||
| + | step 67: a=1067192296302822 b=12163912033773 | ||
| + | step 68: a=1055028384269049 b=12163912033773 | ||
| + | step 69: a=1042864472235276 b=12163912033773 | ||
| + | step 70: a=1030700560201503 b=12163912033773 | ||
| + | step 71: a=1018536648167730 b=12163912033773 | ||
| + | step 72: a=1006372736133957 b=12163912033773 | ||
| + | step 73: a=994208824100184 b=12163912033773 | ||
| + | step 74: a=982044912066411 b=12163912033773 | ||
| + | step 75: a=969881000032638 b=12163912033773 | ||
| + | step 76: a=957717087998865 b=12163912033773 | ||
| + | step 77: a=945553175965092 b=12163912033773 | ||
| + | step 78: a=933389263931319 b=12163912033773 | ||
| + | step 79: a=921225351897546 b=12163912033773 | ||
| + | step 80: a=909061439863773 b=12163912033773 | ||
| + | step 81: a=896897527830000 b=12163912033773 | ||
| + | step 82: a=884733615796227 b=12163912033773 | ||
| + | step 83: a=872569703762454 b=12163912033773 | ||
| + | step 84: a=860405791728681 b=12163912033773 | ||
| + | step 85: a=848241879694908 b=12163912033773 | ||
| + | step 86: a=836077967661135 b=12163912033773 | ||
| + | step 87: a=823914055627362 b=12163912033773 | ||
| + | step 88: a=811750143593589 b=12163912033773 | ||
| + | step 89: a=799586231559816 b=12163912033773 | ||
| + | step 90: a=787422319526043 b=12163912033773 | ||
| + | step 91: a=775258407492270 b=12163912033773 | ||
| + | step 92: a=763094495458497 b=12163912033773 | ||
| + | step 93: a=750930583424724 b=12163912033773 | ||
| + | step 94: a=738766671390951 b=12163912033773 | ||
| + | step 95: a=726602759357178 b=12163912033773 | ||
| + | step 96: a=714438847323405 b=12163912033773 | ||
| + | step 97: a=702274935289632 b=12163912033773 | ||
| + | step 98: a=690111023255859 b=12163912033773 | ||
| + | step 99: a=677947111222086 b=12163912033773 | ||
| + | step 100: a=665783199188313 b=12163912033773 | ||
| + | step 101: a=653619287154540 b=12163912033773 | ||
| + | step 102: a=641455375120767 b=12163912033773 | ||
| + | step 103: a=629291463086994 b=12163912033773 | ||
| + | step 104: a=617127551053221 b=12163912033773 | ||
| + | step 105: a=604963639019448 b=12163912033773 | ||
| + | step 106: a=592799726985675 b=12163912033773 | ||
| + | step 107: a=580635814951902 b=12163912033773 | ||
| + | step 108: a=568471902918129 b=12163912033773 | ||
| + | step 109: a=556307990884356 b=12163912033773 | ||
| + | step 110: a=544144078850583 b=12163912033773 | ||
| + | step 111: a=531980166816810 b=12163912033773 | ||
| + | step 112: a=519816254783037 b=12163912033773 | ||
| + | step 113: a=507652342749264 b=12163912033773 | ||
| + | step 114: a=495488430715491 b=12163912033773 | ||
| + | step 115: a=483324518681718 b=12163912033773 | ||
| + | step 116: a=471160606647945 b=12163912033773 | ||
| + | step 117: a=458996694614172 b=12163912033773 | ||
| + | step 118: a=446832782580399 b=12163912033773 | ||
| + | step 119: a=434668870546626 b=12163912033773 | ||
| + | step 120: a=422504958512853 b=12163912033773 | ||
| + | step 121: a=410341046479080 b=12163912033773 | ||
| + | step 122: a=398177134445307 b=12163912033773 | ||
| + | step 123: a=386013222411534 b=12163912033773 | ||
| + | step 124: a=373849310377761 b=12163912033773 | ||
| + | step 125: a=361685398343988 b=12163912033773 | ||
| + | step 126: a=349521486310215 b=12163912033773 | ||
| + | step 127: a=337357574276442 b=12163912033773 | ||
| + | step 128: a=325193662242669 b=12163912033773 | ||
| + | step 129: a=313029750208896 b=12163912033773 | ||
| + | step 130: a=300865838175123 b=12163912033773 | ||
| + | step 131: a=288701926141350 b=12163912033773 | ||
| + | step 132: a=276538014107577 b=12163912033773 | ||
| + | step 133: a=264374102073804 b=12163912033773 | ||
| + | step 134: a=252210190040031 b=12163912033773 | ||
| + | step 135: a=240046278006258 b=12163912033773 | ||
| + | step 136: a=227882365972485 b=12163912033773 | ||
| + | step 137: a=215718453938712 b=12163912033773 | ||
| + | step 138: a=203554541904939 b=12163912033773 | ||
| + | step 139: a=191390629871166 b=12163912033773 | ||
| + | step 140: a=179226717837393 b=12163912033773 | ||
| + | step 141: a=167062805803620 b=12163912033773 | ||
| + | step 142: a=154898893769847 b=12163912033773 | ||
| + | step 143: a=142734981736074 b=12163912033773 | ||
| + | step 144: a=130571069702301 b=12163912033773 | ||
| + | step 145: a=118407157668528 b=12163912033773 | ||
| + | step 146: a=106243245634755 b=12163912033773 | ||
| + | step 147: a=94079333600982 b=12163912033773 | ||
| + | step 148: a=81915421567209 b=12163912033773 | ||
| + | step 149: a=69751509533436 b=12163912033773 | ||
| + | step 150: a=57587597499663 b=12163912033773 | ||
| + | step 151: a=45423685465890 b=12163912033773 | ||
| + | step 152: a=33259773432117 b=12163912033773 | ||
| + | step 153: a=21095861398344 b=12163912033773 | ||
| + | step 154: a=8931949364571 b=12163912033773 | ||
| + | step 155: a=8931949364571 b=3231962669202 | ||
| + | step 156: a=5699986695369 b=3231962669202 | ||
| + | step 157: a=2468024026167 b=3231962669202 | ||
| + | step 158: a=2468024026167 b=763938643035 | ||
| + | step 159: a=1704085383132 b=763938643035 | ||
| + | step 160: a=940146740097 b=763938643035 | ||
| + | step 161: a=176208097062 b=763938643035 | ||
| + | step 162: a=176208097062 b=587730545973 | ||
| + | step 163: a=176208097062 b=411522448911 | ||
| + | step 164: a=176208097062 b=235314351849 | ||
| + | step 165: a=176208097062 b=59106254787 | ||
| + | step 166: a=117101842275 b=59106254787 | ||
| + | step 167: a=57995587488 b=59106254787 | ||
| + | step 168: a=57995587488 b=1110667299 | ||
| + | step 169: a=56884920189 b=1110667299 | ||
| + | step 170: a=55774252890 b=1110667299 | ||
| + | step 171: a=54663585591 b=1110667299 | ||
| + | step 172: a=53552918292 b=1110667299 | ||
| + | step 173: a=52442250993 b=1110667299 | ||
| + | step 174: a=51331583694 b=1110667299 | ||
| + | step 175: a=50220916395 b=1110667299 | ||
| + | step 176: a=49110249096 b=1110667299 | ||
| + | step 177: a=47999581797 b=1110667299 | ||
| + | step 178: a=46888914498 b=1110667299 | ||
| + | step 179: a=45778247199 b=1110667299 | ||
| + | step 180: a=44667579900 b=1110667299 | ||
| + | step 181: a=43556912601 b=1110667299 | ||
| + | step 182: a=42446245302 b=1110667299 | ||
| + | step 183: a=41335578003 b=1110667299 | ||
| + | step 184: a=40224910704 b=1110667299 | ||
| + | step 185: a=39114243405 b=1110667299 | ||
| + | step 186: a=38003576106 b=1110667299 | ||
| + | step 187: a=36892908807 b=1110667299 | ||
| + | step 188: a=35782241508 b=1110667299 | ||
| + | step 189: a=34671574209 b=1110667299 | ||
| + | step 190: a=33560906910 b=1110667299 | ||
| + | step 191: a=32450239611 b=1110667299 | ||
| + | step 192: a=31339572312 b=1110667299 | ||
| + | step 193: a=30228905013 b=1110667299 | ||
| + | step 194: a=29118237714 b=1110667299 | ||
| + | step 195: a=28007570415 b=1110667299 | ||
| + | step 196: a=26896903116 b=1110667299 | ||
| + | step 197: a=25786235817 b=1110667299 | ||
| + | step 198: a=24675568518 b=1110667299 | ||
| + | step 199: a=23564901219 b=1110667299 | ||
| + | step 200: a=22454233920 b=1110667299 | ||
| + | step 201: a=21343566621 b=1110667299 | ||
| + | step 202: a=20232899322 b=1110667299 | ||
| + | step 203: a=19122232023 b=1110667299 | ||
| + | step 204: a=18011564724 b=1110667299 | ||
| + | step 205: a=16900897425 b=1110667299 | ||
| + | step 206: a=15790230126 b=1110667299 | ||
| + | step 207: a=14679562827 b=1110667299 | ||
| + | step 208: a=13568895528 b=1110667299 | ||
| + | step 209: a=12458228229 b=1110667299 | ||
| + | step 210: a=11347560930 b=1110667299 | ||
| + | step 211: a=10236893631 b=1110667299 | ||
| + | step 212: a=9126226332 b=1110667299 | ||
| + | step 213: a=8015559033 b=1110667299 | ||
| + | step 214: a=6904891734 b=1110667299 | ||
| + | step 215: a=5794224435 b=1110667299 | ||
| + | step 216: a=4683557136 b=1110667299 | ||
| + | step 217: a=3572889837 b=1110667299 | ||
| + | step 218: a=2462222538 b=1110667299 | ||
| + | step 219: a=1351555239 b=1110667299 | ||
| + | step 220: a=240887940 b=1110667299 | ||
| + | step 221: a=240887940 b=869779359 | ||
| + | step 222: a=240887940 b=628891419 | ||
| + | step 223: a=240887940 b=388003479 | ||
| + | step 224: a=240887940 b=147115539 | ||
| + | step 225: a=93772401 b=147115539 | ||
| + | step 226: a=93772401 b=53343138 | ||
| + | step 227: a=40429263 b=53343138 | ||
| + | step 228: a=40429263 b=12913875 | ||
| + | step 229: a=27515388 b=12913875 | ||
| + | step 230: a=14601513 b=12913875 | ||
| + | step 231: a=1687638 b=12913875 | ||
| + | step 232: a=1687638 b=11226237 | ||
| + | step 233: a=1687638 b=9538599 | ||
| + | step 234: a=1687638 b=7850961 | ||
| + | step 235: a=1687638 b=6163323 | ||
| + | step 236: a=1687638 b=4475685 | ||
| + | step 237: a=1687638 b=2788047 | ||
| + | step 238: a=1687638 b=1100409 | ||
| + | step 239: a=587229 b=1100409 | ||
| + | step 240: a=587229 b=513180 | ||
| + | step 241: a=74049 b=513180 | ||
| + | step 242: a=74049 b=439131 | ||
| + | step 243: a=74049 b=365082 | ||
| + | step 244: a=74049 b=291033 | ||
| + | step 245: a=74049 b=216984 | ||
| + | step 246: a=74049 b=142935 | ||
| + | step 247: a=74049 b=68886 | ||
| + | step 248: a=5163 b=68886 | ||
| + | step 249: a=5163 b=63723 | ||
| + | step 250: a=5163 b=58560 | ||
| + | step 251: a=5163 b=53397 | ||
| + | step 252: a=5163 b=48234 | ||
| + | step 253: a=5163 b=43071 | ||
| + | step 254: a=5163 b=37908 | ||
| + | step 255: a=5163 b=32745 | ||
| + | step 256: a=5163 b=27582 | ||
| + | step 257: a=5163 b=22419 | ||
| + | step 258: a=5163 b=17256 | ||
| + | step 259: a=5163 b=12093 | ||
| + | step 260: a=5163 b=6930 | ||
| + | step 261: a=5163 b=1767 | ||
| + | step 262: a=3396 b=1767 | ||
| + | step 263: a=1629 b=1767 | ||
| + | step 264: a=1629 b=138 | ||
| + | step 265: a=1491 b=138 | ||
| + | step 266: a=1353 b=138 | ||
| + | step 267: a=1215 b=138 | ||
| + | step 268: a=1077 b=138 | ||
| + | step 269: a=939 b=138 | ||
| + | step 270: a=801 b=138 | ||
| + | step 271: a=663 b=138 | ||
| + | step 272: a=525 b=138 | ||
| + | step 273: a=387 b=138 | ||
| + | step 274: a=249 b=138 | ||
| + | step 275: a=111 b=138 | ||
| + | step 276: a=111 b=27 | ||
| + | step 277: a=84 b=27 | ||
| + | step 278: a=57 b=27 | ||
| + | step 279: a=30 b=27 | ||
| + | step 280: a=3 b=27 | ||
| + | step 281: a=3 b=24 | ||
| + | step 282: a=3 b=21 | ||
| + | step 283: a=3 b=18 | ||
| + | step 284: a=3 b=15 | ||
| + | step 285: a=3 b=12 | ||
| + | step 286: a=3 b=9 | ||
| + | step 287: a=3 b=6 | ||
| + | step 288: a=3 b=3 | ||
| + | 3 | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | This goes reasonably fast, but still requires | ||
| + | |||
| + | <syntaxhighlight lang="python"> | ||
| + | function euclidlamegcd(a,b) | ||
| + | i=0; | ||
| + | while min(a,b)!=0 | ||
| + | if a > b | ||
| + | a = a%b | ||
| + | elseif a < b | ||
| + | b = b%a | ||
| + | end | ||
| + | i+=1; | ||
| + | println("step $(i): a=$(a) b=$(b)") | ||
| + | end | ||
| + | a | ||
| + | end | ||
| + | </syntaxhighlight> | ||
| + | Much of the rest of the course will in implementing such numerical algorithms, to tackle mathematical questions. In fact, the name "algorithm" itself comes from Muḥammad ibn Mūsā al-Khwārizmī, whom we already met in our [[Mathematics]] lectures when discussing algebra. We will see in particular how to find roots of nonlinear equations, differentiate and integrate, interpolate and extrapolate, solve differential equations, etc., but it would wrong to reduce algorithms and computer science to mathematical tasks of this type. In fact, we shall devote the next lecture to particular non-mathematical algorithms which Physicists should know about, because their tasks relate to physical concepts, or simply due to their importance. | ||
=== Links === | === Links === | ||
Revision as of 15:28, 1 March 2021
Crash Course in Scientific Computing
7. Algorithms: the idea
An algorithm is a recipe to solve a problem with a computer, a list of instructions for the later to follow that will bring it to the solution, which it can duly report. Problems are of all types, from scientific problems such as finding roots of complex functions to integrating differential equations passing by everybody's daily problems such as finding the shortest or best route to bring you from A to B in a complex map or sorting the list of top results in an internet query. The set of instructions can be efficient and lead to a rapid, accurate and faithful solution from the computer, or on the opposite, clumsy, redundant and leading it to waste resources and possibly not even the best, or a good, or even any solution at all. The art of finding a good algorithm has been guiding scientists and engineers since antiquity. Any single problem typically comes with a myriad of different algorithms. For many problems, such as integer factorization, we do not have yet, and probably will never have, good algorithms which can perform the job in a reasonable time. This is the basis for today's cryptography.
One of the simplest algorithms is to find the largest number in a list that has no particular order. We will use this as a starting point to illustrate the above concepts. It is a simple algorithm because its best implementation is basically what one would do anyway: go through each element in turn, if the element we currently examine is larger than the largest we found so far, we update our record, if not, we carry on. Here's a Julia implementation:
function myfindmax(lst) i=1; imax=length(lst); lmax=lst[1] while i<imax i+=1; if lst[i]>lmax lmax=lst[i] end end lmax end
Example application:
julia> myfindmax(rand(10)) 0.985052934036265
Although in principle it is better to test your algorithm on cases which you know and that you can check yourself by hand:
julia> known=rand(Int8, 5) 5-element Array{Int8,1}: -13 -94 22 90 -86 julia> myfindmax(known) 90 julia> myfindmax(abs.(known)) 94
It is also good to test on particular as well as extreme cases, e.g., when the max element is first or last. For instance, if we would have specified the increment i+=1 after the test, the algorithm would fail if the max would find itself as the last element of the array (which would be the case if the list would be ordered):
julia> myfindmax([i for i=1:10]) 10
An important aspect of algorithms is their efficiency, how fast and good they are in performing the job. To benchmark, one can use @time or, if wanting to store the result for later processing, @elapsed (!!):
julia> mytime=zeros(100); julia> for i=1:100 lst = rand(10^6) mytime[i] = @elapsed myfindmax(lst); end julia> comptime=zeros(100); julia> for i=1:100 lst = rand(10^6) comptime[i] = @elapsed maximum(lst); end julia> plot([mytime comptime], label=["us" "julia"])
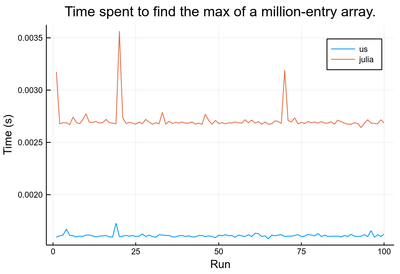
As an exception to the general rule, we find here that our own implementation is actually faster than the one provided by the system:
julia> mean(mytime) 0.0016102164000000002 julia> mean(comptime) 0.0027113203900000003
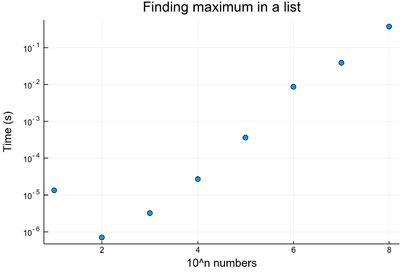
The "complexity" of our find-max algorithm is linear: it grows in direct proportion to the size of the input, as can be understood easily from the way the algorithm is designed. Here is this relationship explictely calculated by the computer:
julia> lt=[@elapsed myfindmax(rand(10^i)) for i=1:8] julia> scatter(lt, yscale=:log10, xlabel="10^n numbers", ylabel="Time (s)", title="Finding maximum in a list", legend=false)
To do even more advanced benchmarking, one can be
julia> using BenchmarkToolsjulia> @benchmark myfindmax(rand(10^6)) BenchmarkTools.Trial: memory estimate: 7.63 MiB allocs estimate: 2 -------------- minimum time: 2.015 ms (0.00% GC) median time: 2.061 ms (0.00% GC) mean time: 2.184 ms (4.24% GC) maximum time: 42.876 ms (88.56% GC) -------------- samples: 2285 evals/sample: 1 julia> @benchmark maximum(rand(10^6)) BenchmarkTools.Trial: memory estimate: 7.63 MiB allocs estimate: 2 -------------- minimum time: 3.344 ms (0.00% GC) median time: 3.461 ms (0.00% GC) mean time: 3.570 ms (3.05% GC) maximum time: 44.792 ms (91.19% GC) -------------- samples: 1399 evals/sample: 1
The fact that our readily-made version is faster than the one provided by the system has been flagged by the Julia community and has been traced to time being lost when checking for NaN numbers.
Algorithms usually rely on tricks or clever observations. For instance, whatever the numbers $y$ and $x$, it is always true that $\sqrt{x}$ is comprised between $y$ and $x/y$. This is easy to prove and follow from the fact that $1/\sqrt{x}=\sqrt{x}/x$. If $y<\sqrt{x}$, then $1/y>\sqrt{x}/x$ which brings us to
$$y<\sqrt{x}<x/y$$
while if $y>\sqrt{x}$ then, similarly, $1/y<\sqrt{x}/x$ and we have the opposite inequality
$$x/y<\sqrt{x}<y$$
So given to numbers $x$ and $y$, a good guess to approximate $\sqrt{x}$ is to take their average ${1\over2}(y+x/y)$. We now have a number closer to $\sqrt{x}$, so we can simply iterate. This is, thus, our algorithm, start with any $y_0\neq x$ and compute:
$$y_{n+1}={1\over2}\left(y_n+{x\over y_n}\right)$$
This will converge to $\sqrt{x}$. This method was known to the Babylonians to compute $\sqrt{2}$. This is the Julia code:
julia> x=2; y=1; julia> while abs(y^2-x)>10^-12 global y=(1/2)*(y+x/y) println(y) end 1.5 1.4166666666666665 1.4142156862745097 1.4142135623746899 1.414213562373095 julia> √2 1.4142135623730951
This is frustratingly fast! Numerical analysis shows that the number of significant digits doubles at each step. We don't need any better algorithm than this one designed by the Babylonians, and this is actually the steps that are undertaken by your pocket calculator, or any computer for that matter, when you press the √ button. Wherever it starts from, in just a few steps, it will have all the decimals of its accuracy correct to the sought square root. So now you how this happens. Let us see other implementations of important operations.
Sieve of Eratosthenes
Find the largest prime below 1,000,000,000
Answer: This is 999,999,937
Division algorithm/Euclidean algorithm
Euclidean—or integer—division takes two (positive, without loss of generality) integers $a$ (numerator) and $b$ (denominator) and returns another two integers: $q$ (quotient) and $r$ (remainder)
$$a=bq+r$$
with $0\ge q<p$. We have seen that julia computes these quantities directly so there is no need of an algorithm per se:
julia> function juliadiv(a,b) [a÷b, a%b] end
but to illustrate the point, let us look at various implementations. The oldest one is from Euclid himself, in his Elements, Book VII, Proposition 1, a simple method is proposed: starting with $r=a$, while $r\ge b$, subtract $b$ from $r$ and take this as the new $r$ and when this is not possible, what is left is the final remainder $r$. The number of times it took to get there is $q$. In julia code:
function eucliddiv(a,b) r=a q=0 while r-b ≥ 0 q+=1 r=r-b end [q r] end
This is very simple but can get quite lengthy. One would use long division algorithms for faster results. Instead of looking at those now, we turn to an important historical algorithm, Euclid's algorithm, which computes the gcd (greatest common divisor between two numbers). This is one of the oldest known algorithms. It is based one the fact that the gcd of two numbers is the same as the gcd of the smaller number with the positive difference of the numbers, so that by iterations, one can decrease the values of the numbers until they become equal, at which point the value thus found is the gcd. This is a julia implementation:
function euclidgcd(a,b) while a!=b if a > b a = a-b elseif a < b b = b-a end end a end
This is the result, showing the details of the intermediate steps:
function euclidgcd(a,b) i=0; while a!=b if a > b a = a-b elseif a < b b = b-a end i+=1; println("step $(i): a=$(a) b=$(b)") end a end
julia> euclidgcd(abs(rand(Int)), abs(rand(Int))) step 1: a=1695854002851361803 b=4884762153376862325 step 2: a=1695854002851361803 b=3188908150525500522 step 3: a=1695854002851361803 b=1493054147674138719 step 4: a=202799855177223084 b=1493054147674138719 step 5: a=202799855177223084 b=1290254292496915635 step 6: a=202799855177223084 b=1087454437319692551 step 7: a=202799855177223084 b=884654582142469467 step 8: a=202799855177223084 b=681854726965246383 step 9: a=202799855177223084 b=479054871788023299 step 10: a=202799855177223084 b=276255016610800215 step 11: a=202799855177223084 b=73455161433577131 step 12: a=129344693743645953 b=73455161433577131 step 13: a=55889532310068822 b=73455161433577131 step 14: a=55889532310068822 b=17565629123508309 step 15: a=38323903186560513 b=17565629123508309 step 16: a=20758274063052204 b=17565629123508309 step 17: a=3192644939543895 b=17565629123508309 step 18: a=3192644939543895 b=14372984183964414 step 19: a=3192644939543895 b=11180339244420519 step 20: a=3192644939543895 b=7987694304876624 step 21: a=3192644939543895 b=4795049365332729 step 22: a=3192644939543895 b=1602404425788834 step 23: a=1590240513755061 b=1602404425788834 step 24: a=1590240513755061 b=12163912033773 step 25: a=1578076601721288 b=12163912033773 step 26: a=1565912689687515 b=12163912033773 step 27: a=1553748777653742 b=12163912033773 step 28: a=1541584865619969 b=12163912033773 step 29: a=1529420953586196 b=12163912033773 step 30: a=1517257041552423 b=12163912033773 step 31: a=1505093129518650 b=12163912033773 step 32: a=1492929217484877 b=12163912033773 step 33: a=1480765305451104 b=12163912033773 step 34: a=1468601393417331 b=12163912033773 step 35: a=1456437481383558 b=12163912033773 step 36: a=1444273569349785 b=12163912033773 step 37: a=1432109657316012 b=12163912033773 step 38: a=1419945745282239 b=12163912033773 step 39: a=1407781833248466 b=12163912033773 step 40: a=1395617921214693 b=12163912033773 step 41: a=1383454009180920 b=12163912033773 step 42: a=1371290097147147 b=12163912033773 step 43: a=1359126185113374 b=12163912033773 step 44: a=1346962273079601 b=12163912033773 step 45: a=1334798361045828 b=12163912033773 step 46: a=1322634449012055 b=12163912033773 step 47: a=1310470536978282 b=12163912033773 step 48: a=1298306624944509 b=12163912033773 step 49: a=1286142712910736 b=12163912033773 step 50: a=1273978800876963 b=12163912033773 step 51: a=1261814888843190 b=12163912033773 step 52: a=1249650976809417 b=12163912033773 step 53: a=1237487064775644 b=12163912033773 step 54: a=1225323152741871 b=12163912033773 step 55: a=1213159240708098 b=12163912033773 step 56: a=1200995328674325 b=12163912033773 step 57: a=1188831416640552 b=12163912033773 step 58: a=1176667504606779 b=12163912033773 step 59: a=1164503592573006 b=12163912033773 step 60: a=1152339680539233 b=12163912033773 step 61: a=1140175768505460 b=12163912033773 step 62: a=1128011856471687 b=12163912033773 step 63: a=1115847944437914 b=12163912033773 step 64: a=1103684032404141 b=12163912033773 step 65: a=1091520120370368 b=12163912033773 step 66: a=1079356208336595 b=12163912033773 step 67: a=1067192296302822 b=12163912033773 step 68: a=1055028384269049 b=12163912033773 step 69: a=1042864472235276 b=12163912033773 step 70: a=1030700560201503 b=12163912033773 step 71: a=1018536648167730 b=12163912033773 step 72: a=1006372736133957 b=12163912033773 step 73: a=994208824100184 b=12163912033773 step 74: a=982044912066411 b=12163912033773 step 75: a=969881000032638 b=12163912033773 step 76: a=957717087998865 b=12163912033773 step 77: a=945553175965092 b=12163912033773 step 78: a=933389263931319 b=12163912033773 step 79: a=921225351897546 b=12163912033773 step 80: a=909061439863773 b=12163912033773 step 81: a=896897527830000 b=12163912033773 step 82: a=884733615796227 b=12163912033773 step 83: a=872569703762454 b=12163912033773 step 84: a=860405791728681 b=12163912033773 step 85: a=848241879694908 b=12163912033773 step 86: a=836077967661135 b=12163912033773 step 87: a=823914055627362 b=12163912033773 step 88: a=811750143593589 b=12163912033773 step 89: a=799586231559816 b=12163912033773 step 90: a=787422319526043 b=12163912033773 step 91: a=775258407492270 b=12163912033773 step 92: a=763094495458497 b=12163912033773 step 93: a=750930583424724 b=12163912033773 step 94: a=738766671390951 b=12163912033773 step 95: a=726602759357178 b=12163912033773 step 96: a=714438847323405 b=12163912033773 step 97: a=702274935289632 b=12163912033773 step 98: a=690111023255859 b=12163912033773 step 99: a=677947111222086 b=12163912033773 step 100: a=665783199188313 b=12163912033773 step 101: a=653619287154540 b=12163912033773 step 102: a=641455375120767 b=12163912033773 step 103: a=629291463086994 b=12163912033773 step 104: a=617127551053221 b=12163912033773 step 105: a=604963639019448 b=12163912033773 step 106: a=592799726985675 b=12163912033773 step 107: a=580635814951902 b=12163912033773 step 108: a=568471902918129 b=12163912033773 step 109: a=556307990884356 b=12163912033773 step 110: a=544144078850583 b=12163912033773 step 111: a=531980166816810 b=12163912033773 step 112: a=519816254783037 b=12163912033773 step 113: a=507652342749264 b=12163912033773 step 114: a=495488430715491 b=12163912033773 step 115: a=483324518681718 b=12163912033773 step 116: a=471160606647945 b=12163912033773 step 117: a=458996694614172 b=12163912033773 step 118: a=446832782580399 b=12163912033773 step 119: a=434668870546626 b=12163912033773 step 120: a=422504958512853 b=12163912033773 step 121: a=410341046479080 b=12163912033773 step 122: a=398177134445307 b=12163912033773 step 123: a=386013222411534 b=12163912033773 step 124: a=373849310377761 b=12163912033773 step 125: a=361685398343988 b=12163912033773 step 126: a=349521486310215 b=12163912033773 step 127: a=337357574276442 b=12163912033773 step 128: a=325193662242669 b=12163912033773 step 129: a=313029750208896 b=12163912033773 step 130: a=300865838175123 b=12163912033773 step 131: a=288701926141350 b=12163912033773 step 132: a=276538014107577 b=12163912033773 step 133: a=264374102073804 b=12163912033773 step 134: a=252210190040031 b=12163912033773 step 135: a=240046278006258 b=12163912033773 step 136: a=227882365972485 b=12163912033773 step 137: a=215718453938712 b=12163912033773 step 138: a=203554541904939 b=12163912033773 step 139: a=191390629871166 b=12163912033773 step 140: a=179226717837393 b=12163912033773 step 141: a=167062805803620 b=12163912033773 step 142: a=154898893769847 b=12163912033773 step 143: a=142734981736074 b=12163912033773 step 144: a=130571069702301 b=12163912033773 step 145: a=118407157668528 b=12163912033773 step 146: a=106243245634755 b=12163912033773 step 147: a=94079333600982 b=12163912033773 step 148: a=81915421567209 b=12163912033773 step 149: a=69751509533436 b=12163912033773 step 150: a=57587597499663 b=12163912033773 step 151: a=45423685465890 b=12163912033773 step 152: a=33259773432117 b=12163912033773 step 153: a=21095861398344 b=12163912033773 step 154: a=8931949364571 b=12163912033773 step 155: a=8931949364571 b=3231962669202 step 156: a=5699986695369 b=3231962669202 step 157: a=2468024026167 b=3231962669202 step 158: a=2468024026167 b=763938643035 step 159: a=1704085383132 b=763938643035 step 160: a=940146740097 b=763938643035 step 161: a=176208097062 b=763938643035 step 162: a=176208097062 b=587730545973 step 163: a=176208097062 b=411522448911 step 164: a=176208097062 b=235314351849 step 165: a=176208097062 b=59106254787 step 166: a=117101842275 b=59106254787 step 167: a=57995587488 b=59106254787 step 168: a=57995587488 b=1110667299 step 169: a=56884920189 b=1110667299 step 170: a=55774252890 b=1110667299 step 171: a=54663585591 b=1110667299 step 172: a=53552918292 b=1110667299 step 173: a=52442250993 b=1110667299 step 174: a=51331583694 b=1110667299 step 175: a=50220916395 b=1110667299 step 176: a=49110249096 b=1110667299 step 177: a=47999581797 b=1110667299 step 178: a=46888914498 b=1110667299 step 179: a=45778247199 b=1110667299 step 180: a=44667579900 b=1110667299 step 181: a=43556912601 b=1110667299 step 182: a=42446245302 b=1110667299 step 183: a=41335578003 b=1110667299 step 184: a=40224910704 b=1110667299 step 185: a=39114243405 b=1110667299 step 186: a=38003576106 b=1110667299 step 187: a=36892908807 b=1110667299 step 188: a=35782241508 b=1110667299 step 189: a=34671574209 b=1110667299 step 190: a=33560906910 b=1110667299 step 191: a=32450239611 b=1110667299 step 192: a=31339572312 b=1110667299 step 193: a=30228905013 b=1110667299 step 194: a=29118237714 b=1110667299 step 195: a=28007570415 b=1110667299 step 196: a=26896903116 b=1110667299 step 197: a=25786235817 b=1110667299 step 198: a=24675568518 b=1110667299 step 199: a=23564901219 b=1110667299 step 200: a=22454233920 b=1110667299 step 201: a=21343566621 b=1110667299 step 202: a=20232899322 b=1110667299 step 203: a=19122232023 b=1110667299 step 204: a=18011564724 b=1110667299 step 205: a=16900897425 b=1110667299 step 206: a=15790230126 b=1110667299 step 207: a=14679562827 b=1110667299 step 208: a=13568895528 b=1110667299 step 209: a=12458228229 b=1110667299 step 210: a=11347560930 b=1110667299 step 211: a=10236893631 b=1110667299 step 212: a=9126226332 b=1110667299 step 213: a=8015559033 b=1110667299 step 214: a=6904891734 b=1110667299 step 215: a=5794224435 b=1110667299 step 216: a=4683557136 b=1110667299 step 217: a=3572889837 b=1110667299 step 218: a=2462222538 b=1110667299 step 219: a=1351555239 b=1110667299 step 220: a=240887940 b=1110667299 step 221: a=240887940 b=869779359 step 222: a=240887940 b=628891419 step 223: a=240887940 b=388003479 step 224: a=240887940 b=147115539 step 225: a=93772401 b=147115539 step 226: a=93772401 b=53343138 step 227: a=40429263 b=53343138 step 228: a=40429263 b=12913875 step 229: a=27515388 b=12913875 step 230: a=14601513 b=12913875 step 231: a=1687638 b=12913875 step 232: a=1687638 b=11226237 step 233: a=1687638 b=9538599 step 234: a=1687638 b=7850961 step 235: a=1687638 b=6163323 step 236: a=1687638 b=4475685 step 237: a=1687638 b=2788047 step 238: a=1687638 b=1100409 step 239: a=587229 b=1100409 step 240: a=587229 b=513180 step 241: a=74049 b=513180 step 242: a=74049 b=439131 step 243: a=74049 b=365082 step 244: a=74049 b=291033 step 245: a=74049 b=216984 step 246: a=74049 b=142935 step 247: a=74049 b=68886 step 248: a=5163 b=68886 step 249: a=5163 b=63723 step 250: a=5163 b=58560 step 251: a=5163 b=53397 step 252: a=5163 b=48234 step 253: a=5163 b=43071 step 254: a=5163 b=37908 step 255: a=5163 b=32745 step 256: a=5163 b=27582 step 257: a=5163 b=22419 step 258: a=5163 b=17256 step 259: a=5163 b=12093 step 260: a=5163 b=6930 step 261: a=5163 b=1767 step 262: a=3396 b=1767 step 263: a=1629 b=1767 step 264: a=1629 b=138 step 265: a=1491 b=138 step 266: a=1353 b=138 step 267: a=1215 b=138 step 268: a=1077 b=138 step 269: a=939 b=138 step 270: a=801 b=138 step 271: a=663 b=138 step 272: a=525 b=138 step 273: a=387 b=138 step 274: a=249 b=138 step 275: a=111 b=138 step 276: a=111 b=27 step 277: a=84 b=27 step 278: a=57 b=27 step 279: a=30 b=27 step 280: a=3 b=27 step 281: a=3 b=24 step 282: a=3 b=21 step 283: a=3 b=18 step 284: a=3 b=15 step 285: a=3 b=12 step 286: a=3 b=9 step 287: a=3 b=6 step 288: a=3 b=3 3
This goes reasonably fast, but still requires
function euclidlamegcd(a,b) i=0; while min(a,b)!=0 if a > b a = a%b elseif a < b b = b%a end i+=1; println("step $(i): a=$(a) b=$(b)") end a end
Much of the rest of the course will in implementing such numerical algorithms, to tackle mathematical questions. In fact, the name "algorithm" itself comes from Muḥammad ibn Mūsā al-Khwārizmī, whom we already met in our Mathematics lectures when discussing algebra. We will see in particular how to find roots of nonlinear equations, differentiate and integrate, interpolate and extrapolate, solve differential equations, etc., but it would wrong to reduce algorithms and computer science to mathematical tasks of this type. In fact, we shall devote the next lecture to particular non-mathematical algorithms which Physicists should know about, because their tasks relate to physical concepts, or simply due to their importance.