Lorentzians

The Lorentzian is a fundamental distribution function. It is called like that in Physics, in Mathematics it is usually known as the Cauchy distribution. The normalized distribution $f$ with full-width at half maximum $\gamma$ reads, as a function of the variable $\omega$:

$$f(\omega)=\frac{1}{\pi}\frac{\gamma/2}{(\gamma/2)^2+\omega^2}\,.$$

It is the distribution of a memoryless random process. For instance a radioactive particle has no memory of how long it has been existing (there is no identity in quantum mechanics). Therefore, its probability to decay is the same at any moment of its lifetime. This results in an exponential decay. The Fourier transform of that is the Lorentzian.

In this regard, is the antagonist of the other fundamental distribution, the Gaussian, also known as the Normal distribution, which is that of statistically accumulated or averaged events. As such it rules the classical world and our daily life.

The Lorentzian distribution also appears as the solution to the differential equation describing forced resonance.

Fat tail

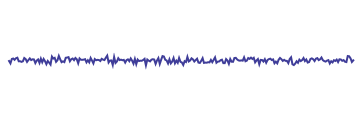
The Lorentzian has interesting counter-intuitive properties, due to its positive kurtosis. Below, for instance, is an example of normally distributed fluctuations:

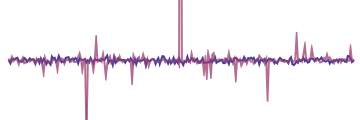
This is what one has in mind when imagining fluctuations, a jerky dance around the mean. Below we now superimpose Lorentzian fluctuations on top of the normal ones:

It looks pretty much the same over some intervals, but displays occasional big departures from the mean. The fluctuator can explore very far. In this comparison, we have truncated the display so that the small fluctuations themselves—which are all there is in the normal case—remain visible.

To get an idea of the dramatic power of the Lorentzian, let us show it again alone, as before (left) and with the full range of fluctuations (right):

Infrequently, but surely, the fluctuator gets arbitrarily far from its mean. In this sense, the Lorentzian is non-classical. We are used, when we think of large fluctuations, of cases like, someone living 120 years. If fluctuations of our lifespan had a fat tail like the Lorentzian, while most of us would still have the same average lifespan, time to time, someone would go on to live for 10000 years.

In the following we collect some useful results which I could not find elsewhere.

Products of Lorentzians

The integrals for some products of Lorentzians (herebelow, all quantities are real):

$$\mathcal{I}_n=\pi\int_{-\infty}^\infty\prod_{i=1}^n\frac{y_i}{(x-x_i)^2+y_i^2}dx\,,$$

can be obtained exactly:

$$\mathcal{I}_1=1\,,$$ $$\mathcal{I}_2=\frac{y_1+y_2}{(x_1-x_2)^2+(y_1+y_2)^2}\,,$$ $$\mathcal{I}_3=\frac{\sum_{i<j}(x_i-x_j)^2y_iy_j+(\sum_iy_i)\prod_{i<j}(y_i+y_j)}{\prod_{i<j}\big((x_i-x_j)^2+(y_i+y_j)^2\big)}\,.$$

Possibly this can be extended to higher values of $n\in\mathbb{N}$.