A mechanism for a perfect single-photon source

⇠ Back to Blog:Science

Ask someone to sketch a stream of photons in time. They will probably do something like this:

This is not incorrect, especially if describing a single-photon source (SPS) where photons are separated from each other. A typical such SPS, however, would more likely look like this:

Still, most people would draw a single-photon source (if you ask for one) as in the first case above. They would do this even in textbooks or in encyclopedias. This is for instance how Mark Fox represents antibunching in his great book, Quantum Optics: (see also Loudon's Fig. 4)

He draws little balls instead—why not?—but we're not the type of people arguing about the representations of the prophet, instead, we're interested on who is the prophet and what he has to say, or, for photons, about their spacing, i.e., about the distribution of their time separations. You will agree that there's a bit of an idealization in this perfect arrangement for the antibunched case. This is how the Wikipedia represents it:

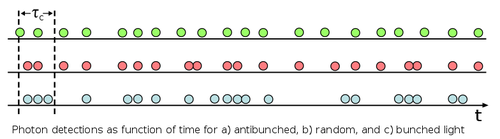
That's closer to the reality for the SPS (green balls), but it looks more like my top stream as opposed to the one I presented as the paradigm of the genre. For the coherent stream (red balls), I wonder if the Author—Jeff Lunden, now head of the @QuantumPhotonic group in Ottawa—did not have also a helping hand, in particular with so-called Poisson bursts, i.e, series of events that are very much closer to each other than you would expect when they are uncorrelated (as they happen to be for a coherent stream). A photon-detective would observe the photon bursts are suspiciously similar, not y-aligned with the rest and in the wrong time order from their overlap, so possibly Dr. Lunden thought the point was not sufficiently illustrated and sneaked in a few, additional bursts, as one could similarly suspect he prettified the SPS so that it does not look as chaotic as mine above, which might be more evocative of chaotic light (that shown in blue).

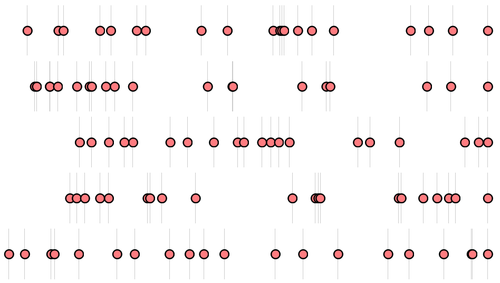
It is also possible that he did nothing of the kind and I'm losing your time on speculations of no importance whatsoever, as it would be a justifiable pedagogical touch, since such Poisson and single-photon streams are close to impossible to faithfully illustrate. Anybody who tried can only sympathize with the illustrator, as it is maddening to show something compelling from Monte Carlo sampling and one typically has to exaggerate or simplify, to make the point across (which is what Physics is, by the way, bringing meaning to idealized, simplified versions of reality). If I give you five (no cheating, no selection of any sort) truly random sampling of 20 Poisson events, this is what one gets:

(and how one can get it, with Mathematica, try it for yourself:)

photon = Graphics[{EdgeForm[{Black, Thickness[.15]}], FaceForm[RGBColor["#FF7C80"]], Disk[]}];
GraphicsColumn[
 Table[lR = Sort[Table[Random[], {i, 20}]]; 
  ListPlot[Partition[Riffle[lR, 0 Range[Length[lR]]], 2], 
   Axes -> False, GridLines -> {lR, {}}, AspectRatio -> .1, 
   ImageSize -> 800, PlotMarkers -> {photon, .2}], {i, 5}]]

As you can see, the last one looks like the Wikipedia antibunching and the previous-to-last one like the Wikipedia bunching, although they are all random, and none really looks like the Wikipedia random case (maybe the third if you would ignore the massive window of no emission at the beginning).

Bortkiewicz.

In any case, one can see that bursts are a true and strong phenomenon of randomness. They even have their quantifier, known as the burstiness. I should delve more into the burstiness of things. The effect was discovered by Ladislaus Bortkiewicz (Борткевич as he was Russian though he lived in Germany and was of Polish ancestry). You might also have heard of him in connection with his "economic theory of Marx", if you're into that sort of thing, but his main claim to fame is to have uncovered a fundamental effect from horse kicks in the Prussian army. His big achievement is the understanding of the law of small numbers, or the probability of very rare events but with much time for them to be realized. The book he wrote about it is where, apparently, the name of the Poisson distribution comes from.

The Poisson distribution itself indeed comes from Siméon Poisson and even from before. I haven't read yet Poisson's book but it seems that he did not consider the law of small numbers, only, and on the opposite, «la loi des grands nombres» (the law of large numbers). So it was quite an insight from Bortkiewicz to uncover Poisson bursts, precisely because this involves small-probability events, for which it was difficult at the time (we're speaking about Prussia) to have the amount of big data needed to extract something significant. But Prussians were precisely the type of people who could compile in 20 volumes of Preussischen Statistik the deaths of officers from horse kicks. Not something that would happen regularly but which, in the course of 20 years as was the timespan considered, can give some statistics. Bortkiewicz later used that to calibrate insurance claims and child suicide data. It remains a hotly debated phenomenon in connection with child deaths in hospitals. These happen, and when they burst, as they must if they are not correlated, of course, everybody freaks out and blames the hospital (this also happens with shark attacks, etc.)

Back to photons: in an uncorrelated stream, which Glauber tells us is what laser light is (no notion of photons in a wave, so forget about their correlations), photon-detection—if you insist in detecting your light in this way—will thus present photon bursts. This is what Jeff highlights when he shows us this

Why I'm spending so much time about this, is because there is a very simple way to connect the Poisson to the (conventional) antibunched stream, which is what we started our discussion with. And this gives much insight into the behavior or structure of the "single photons" from such a stream. By conventional SPS I mean the one you'd get by exciting from time to time a Two-Level System (SPS) and letting it emit a photon as it goes back to its ground state.

When I said that, I said everything. The antibunching emission can be seen as the sum of two Poisson processes: one to excite (randomly) the other to de-excite (also randomly). Such processes over the continuous line (time) are described by the exponential distribution. This is a central distribution in physics as it describes memoryless (i.e., uncorrelated) events. It is, for instance, the physics behind the half-life of radioactive particles (how Carbon-14 dating works, for instance).

Now, whereas the sum of two (discrete) Poisson distributions is also a Poisson distribution, the sum of two (continuous) exponential distributions is something else, known as a Hypoexponential distribution.

Erlang.

For the simplicity of our discussion and the elegance of its illustration, I will assume the rates are the same so that one can refer to the same underlying stream throughout. In this case, the distribution reduces to the so-called Erlang distribution (a special case of the more famous Gamma distribution), which was derived to compute the number of telephone calls made at the same time when people used to have an operator at a switching station.

So if you want to simulate a conventional SPS, simply take a random stream and skip every other "photon", understanding the rejected event as setting the 2LS in its excited state. That's how you get the second stream at the top, the one I told you represents a typical SPS.

While this is a very simple way to look at it, it's also very instructive, because, if you remember the Poisson bursts thing, then you understand that such a "mechanism" will fatally produce photons arbitrarily close in time. It will be rare indeed, but as Bortkiewicz understood with his horse kicks: give it enough time. If you wait long enough, anything can happen. Below, I show strings where one keeps every-other-$(N-1)$ photon from an underlying Poisson stream, meaning that for $N=1$ one keeps all photons, and thus has the original Poisson (uncorrelated, or coherent) stream; The case $N=2$, keeping every other photon (one yes, one no, etc.) yields the conventional SPS (incoherently driven two-level system). This still results in photon bursts, as shown by the horse kicks. Although they tend to get softened, some remain pretty severe.

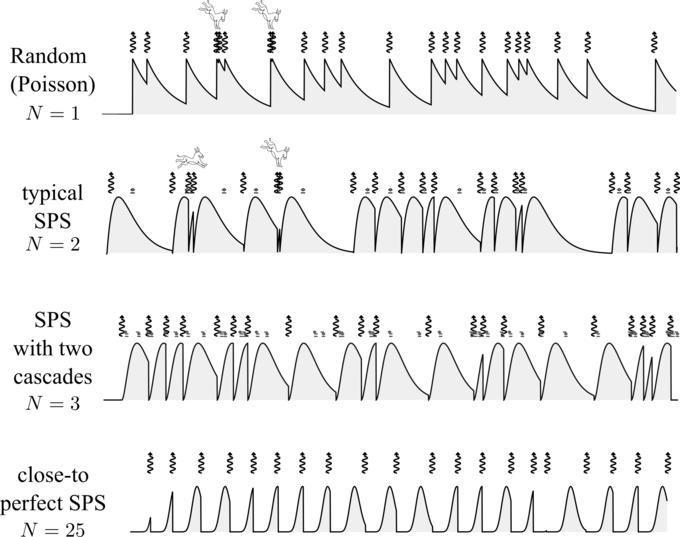
Making a "perfect single-photon source" in the sense of producing single-photons with no overlap whatsoever, has been a goal for many groups. Such groups want to minimize the probability that two photons be detected at exactly the same time, and so they strive to make $g^{(2)}(0)$ as small as possible.

But this is, theoretically, easy to do: the 2LS that gets excited and re-emits already does that, and indeed its $g^{(2)}(\tau)$ is:

$$g^{(2)}(\tau)=1-\exp\big(-2\gamma\tau\big)\tag{1}$$

(assuming again the same rates $\gamma$ for excitaiton and de-excitation). And you can check that $g^{(2)}(0)=0$. So what's the big deal?

The big deal is that a photodetector needs some time to detect the photon. This is not an instantaneous process. Even discussed at a very fundamental level, you have to include a bandwidth $\Gamma$ for the detector. This was highlighted by Eberly and Wòdkiewicz with their introduction of what they called the "physical spectrum of light". They were worrying about time-dependent signals and, as it happens, for stationary signals, their refined treatment is not needed, one gets the same result with the famous Wiener-Khinchin theorem.

For two-photon observables (and higher-order numbers), however, Elena et al. emphasized that in this case, even for stationary signals, one needs to include the detector bandwidth. If you don't do that, you look at a particular and quite unphysical limit of the problem: that of perfect time-resolution. Such a perfect time resolution is tolerable for describing a one-photon observable such as a power spectrum: there, better and better detectors will converge towards Wiener-Khinchin. But at the two-photon level, e.g., when you compute an antibunching, you lose a lot of the physics and trivialize the problem away in the perfect-detector limit. Already ten-years ago, we were drawing attention to so-called two-photon spectra at the two-photon level, and those must be defined in relation to some detector bandwidth. For them, the physical spectrum of Eberly & Wòdkiewicz becomes mandatory. When dealing with two-photons, we are one step deeper into Physics as opposed to Mathematics. In terms of antibunching, it means that one should worry not only about $g^{(2)}(0)$, which is a perfect (unphysical) detector quantity, but to $g^{(2)}(\tau)$ locally around $\tau=0$, as a real detector will be sensible with what is going there.

And what is going on for the conventional SPS is that Poisson bursts will clutter photons there.

So to have a perfect SPS, one should thus open a gap. We analyzed the photon correlations in the particular case of a rigid, constant gap with Sana Khalid, and found that it had interesting features, most prominently, bunching oscillations at later times. We regarded this as a feature, not a bug.

Our Referees (three of them) all complained in one way or the other as to the lack of some underlying mechanism to realize such a gapped source:

• Referee 1:

Being an idealized concept, such perfect single photon source is
never realized in the lab. [...] While no quantum process is described
or known to produce such a source, the results discussed and reported
in this manuscript are still interesting from a theoretical point of view

• Referee 2:

To my opinion, the proposal of perfect single-photon sources
developed in this work is rather philosophical in nature and it does
not contain any concrete indications on how to build such a device or
how to measure its functionality experimentally. This complicates the
judgement about the validity and technical correctness of this
paper.

• Referee 3:

The apparent drawback of the manuscript is that it does not
present any protocol to realize the considered photon stream.

To be fair, only Referee 2 did not recommend publication, thinking that the source was so as wild as to be actually unphysical and pathological, since "localization of a photon in time requires complete uncertainty of its energy [...] using the known relativistic uncertainty relation ΔpΔt\sim\hbar/c, we observe that this implies also complete uncertainty of the momentum of the photon, that is complete uncertainty of the direction of the photon propagation [...] One cannot separate the photons from this source from all other photons because they can possess all energies and can propagate in any direction. The latter is even more restrictive than the former for the usual optical table setups." Put like this, it could indeed frighten an editor, but while consequences of photons-at-all-energies having a bearing on the matter (the comments of this Referee not being as silly as they look) they do not make the source unphysical.

In fact, it is possible to provide a mechanism to approach such a scenario of opening a gap in time, making the photons increasingly repulsive, as much as we want, with the result of their long-time correlations exhibiting the peaks of liquefaction. This simple, basic fundamental, we provide with Eduardo in our latest paper. The idea is as simple as considering not two steps (excitation, de-excitation) but $N$ steps: you excite, and, say, fall down a cascade, until eventual emission. Still keeping all the rates the same, and renormalizing the time so that the brightness is the same for all cases, we get the two bottom row of the previous figure.

Let me show it to you again, but removing the underlying distributions, and the skipped-over events (transiting through the various levels of the $N$-level system):

All those are actual Monte Carlo sampling, straight from the computer to the plot, I didn't cherry-pick or change anything. Again, the top row is random, 2nd row is the conventional SPS, 3rd is with one intermediate cascade and 4th is with 24 intermediate steps. The bottom row is the one I showed you at the beginning, the one that most people would propose as a single-photon source. It is indeed, but not your usual one, it's a 24-steps mechanism. It is what I would qualify as a "perfect single-photon source", with its $g^{(2)}(\tau)$ exhibiting the beautiful oscillations of the pair correlation function of a liquid. Indeed, its two-photon correlation function is not the simple exponential return to normality of Eq. (1), but opens a gap in the form of a flat plateau at small times $\tau$, followed by a sequence of oscillations which denote the onset of time ordering. Because the source is stationary, this describes a liquid, as opposed to a crystal: the order can be extended (the liquid can be viscous) but it ultimately returns to complete randomness. There's only so far one photon can see ahead, in time (this might be due to the dimensionality, I didn't need to highlight that we brought those thermodynamic concepts of phases, crystalization, liquids, etc., into the temporal domain!) That's almost Mark Fox's antibunching, and the one that others would similarly fantasize about. It is, take note, stationary, photons far enough are uncorrelated.

Here is the $g^{(2)}(\tau)$ calculated from 100,000 points similar to the samples of 20 shown above:

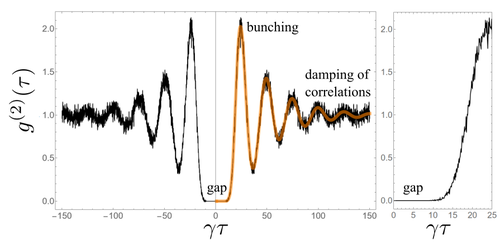
The trace in red is the analytical result, which is a very beautiful (as well as general) expression, valid for any $N$ from $N=1$ for coherent, $N=2$ to the conventional SPS and $25$ the case shown here:

\begin{equation} \tag{2} g^{(2)}_N(\tau) = 1 + \sum_{p=1}^{N-1} z_N^p \exp\big(- \gamma (1- z_N^p)\tau\big) \end{equation}

where~$z_N\equiv\exp\left(i{2\pi/ N}\right)$ are the $N$th roots of unity.

It is interesting to compare the $g^{(2)}(\tau)$ of this—now physical—photon stream, with that of Sana and I's mathematical idealization:

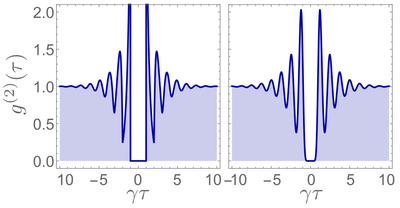
So, while our three Referees complained that we didn't have a mechanism to produce the curve on the left, we have been able, in a few weeks, based on understanding the mechanism, to provide an explicit mechanism that does produce the curve on the right. This is... well, quite compelling, in my humble opinion. From dream to reality. Now it just needs some material scientist, engineer or inventor to find a way to implement it in a structure, and grace the world with a new type of light: single photons!

There is something that you do not see on the analytical formula, but which I want to highlight from the Monte Carlo simulation, regarding the gap. The flat plateau. It is exactly zero. That's not the $g^{(2)}(0)$ that people ramble on being very small, that's the real deal: the exact zero. Let us be accurate here: it is not the mathematical zero like in Ref. , because it's not a non-analytical $g^{(2)}(\tau)=0$ until $t_\mathrm{G}$, which produces the discontinuities you see on the left plot. It is "merely" small enough to be as good as exactly zero. Namely, it is:

\begin{equation} g^{(2)}(\tau)\approx{N^2\over N!}(\gamma\tau)^N \end{equation}

so that for $N=25$, that is a number small enough so that in decades of acquisitions at high repetition rates, you won't get a single coincidence even with an imperfect detector (for $\gamma\tau=1/2$, $g^{(2)}\approx 10^{-30}$). So if not a "mathematical zero", consider it a "physical zero", which you can see in concrete terms from the fact that there is no noise in the gap. It's flat even when including fluctuations! That's as good as a zero can be in the real world.

So there is now a serious contender for a serious "perfect" single-photon source. I remember when Camilo presented his thesis, at the tribunal lunch afterward, one of his examiners told me this was a bit arrogant to refer to our homodyned source as almost "perfect", missing the point that this was not hype, it was conceptual. There'll come a time when an experimentalist will reproduce such a noiseless gap. Until then, I believe all claims of "perfect" single-photon emission (and one does find them), based on deconvolution, time uncertainty, corrections of this or that, etc., are a bit arrogant, i.e., they are wrong.

Now we can have a look back at the literature and see if what people have reported fits somehow with our picture above. All this looks so fundamental, it shouldn't be me to be working out all this. I work on multiphotonics, not on single-photon emission. Oscillations of $g^{(2)}(\tau)$ are, of course, commonplace, simply replacing incoherent excitation with a coherent driving. Then one gets Rabi oscillations of the emitter. To the best of my knowledge, nobody ever linked such oscillations with a higher quality of the source to emit single photons. People prefer the $g^{(2)}(0)$ criterion. Nevertheless, for the same value of $g^{(2)}(0)$, the Rabi case is more resilient than incoherent cases without oscillations.

Bunching elbows of $g^{(2)}(\tau)$ are also familiar, from the snapshots a theorist can have in the back of their mind (I compiled a list in my gallery of antibunching). Prospecting with that objective in mind, I believe the main experimental work in that connection is from Kurtsiefer et al., with their Stable solid-state source of single photons. Not only do they observe this type of bunching, they also work out a nice rate-equation model based on so-called "de-shelving" (meaning, there's an intermediate state getting in the way). Their theoretical analysis was undertaken earlier by Pegg et al. (not known from Kurtsiefer, apparently) in much greater detail, covering various cases and different types of driving.

Interestingly, although the shape appears to be qualitatively similar, it differs in many key aspects. The reason is that, although Pegg et al. refer to "cascades", they consider situations that are better seen as variations of the V and~$\Lambda$ configurations of the three-level system, where the state 0 has two excited states or two ground states. In their cascades, those two states are sandwiching the zero (I refrain from writing "ground" here) state, in particular with pumping terms which kick the excitation from zero to either one or two. In contrast, our cascade is closer to what you expect from the term: something that falls down through the various levels in succession:

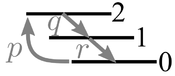
Our case, in the approach of Pegg et al., is described by the rate equations:

\begin{align} \dot\rho_{00}&=r\rho_{11}-p\rho_{00}\,\\ \dot\rho_{11}&=q\rho_{22}-r\rho_{11}\,\\ \dot\rho_{22}&=p\rho_{00}-q\rho_{22}\,, \end{align}

which for initial condition $\rho_{00}(0)=1$ and~$\rho_{11}(0)=\rho_{22}(0)=0$, is easily solved:

\begin{align} {\rho_{00}(t)\over\rho_\mathrm{ss}}=1-e^{-(p+q+r)\frac{t}{2}} \Big\{\frac{p+q+r}{\sqrt{p^2-2 p (q+r)+(q-r)^2}}\sinh\left( \sqrt{p^2-2 p (q+r)+(q-r)^2}\frac{t}{2}\right)\\ +\cosh \left( \sqrt{p^2-2 p (q+r)+(q-r)^2}\frac{t}{2}\right)\Big\} \end{align}

The initial conditions equate this population to $g^{(2)}(t)$. Indeed, setting the parameters $p=q=r$ all equal to $\gamma$, we recover Eq. (7) of our text, i.e. (case $N=3$ of Eq. (2)):

$$g^{(2)}(\tau)=1-2\sin\left({\sqrt3\over 2}\gamma\tau+{\pi\over6}\right)e^{-{3\over2}\gamma\tau}$$

So there are several departures from Pegg et al.'s seminal description: first, we extended the cascades to an arbitrary number of steps; second, we find results with a distinct physical character, namely, liquefaction of the photons in time, with oscillations and flattening of small-time correlations (opening of a gap), all this from an incoherent model.

Interestingly, some people saw such flattening of the small $\tau$ correlations, e.g., Boll et al. report what they call a "rounded shape" for what looks like a $\tau^2$ dependence. This might be because there is a genuine cascade somewhere (maybe inside or between the shelving states)? They attribute it to their detector resolution instead, which could also be investigated in more detail as we have derived exact expressions for such cases.

As a conclusion: every time you hear people speaking about $g^{(2)}(0)$ being very small in a way that suggests they have very good single-photon emission, raise an eyebrow and tell them to be wary of horse-kicks, that $g^{(2)}(0)$ is very treacherous and that one should not turn one's back to a photo-detector any more than you'd do to a Prussian military equidae.

References

— Fabrice • 19:41, 4 February 2024