The pair correlation function

⇠ Back to Blog:Science

All radial distribution functions exhibit their first peak at X=1, decreasing monotonically to the first minimum, which is followed by oscillations of diminishing amplitude resembling those of the experimentally determined radial distribution functions of real liquids.

—Kirkwood on the pair correlation function, Radial Distribution Functions and the Equation of State of a Fluid Composed of Rigid Spherical Molecules. J. G. Kirkwood, E. K. Maun and B. J. Alder in J. Chem. Phys. 18:1040 (1950).

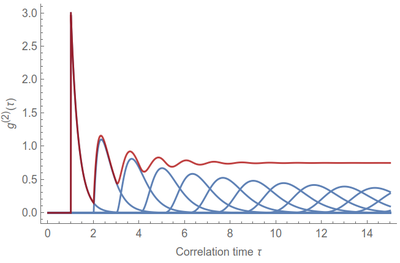
My last paper (to date) describes a particular shape in the correlation of photons which, we argue, is central to characterizing a perfect single-photon source (see also this twitter thread and this one).

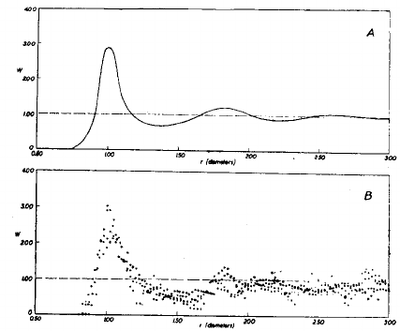
This shape turns out to be, in fact, well-known in condensed matter, physical chemistry and statistical physics. Here you see it from a 1936 paper for mercury (top) and for a macroscopic model of jelly balls suspended in oil (bottom) where it is also mentioned that similar curves are found with steel spheres and even seeds laid down onto a flat surface (if you have access to this paper I'd be happy to see it):

The pair-correlation function, also known as the radial distribution function is an important quantity that can determine the state of a condensed system (gaseous, liquid or solid) by measuring the amount of ordering of its components (e.g., molecules). It enters directly into important properties such as the relative density fluctuation of the fluid, that determines light scattering. In particular, it can be measured through the angular distribution of X-ray scattering, whose Fourier transform gives access to it.

Here it is concisely defined by Kirkwood in one of his many papers on the subject:

Kirkwood (John Gamble)—the K in the BBGKY hierarchy—was one of the authorities in the theory of liquids and a pioneer on the study of correlations in condensed systems. Although a chemist (he won a prize for producing a fiber 1/3 the thickness of silk), he was particularly proficient as a mathematical statistician. He was one of the recruits of Oppenheimer for his Los Alamos team—I don't think he will be in the movie—and amongst those "lucky" to see the first detonation of the H bomb. He is also buried nearby Lars Onsager, so if you go to ever pay tribute to the latter, think of the physical chemist who provided one the earliest "mature" statistical treatment for molecular pair distribution functions, in a 1935, now classic text.

Although the title of this seminal paper gives a focus on mixtures, his insights are more general and best illustrated with a homogeneous system. There he obtains the basic shape of the pair correlation function with a hard sphere model (cf. Section V) even including an attractive potential. The formalism and conceptual framework appear to be more important than the actual result itself, which is modest-looking even at the time, for reasons that we will come back to:

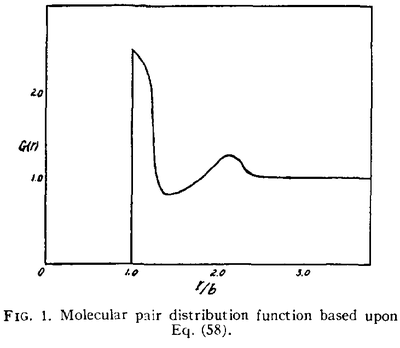
We see in this plot some unmistakable attributes of our shape for the perfect sinle-photon source, in particular the gap. It is interesting that Kirkwood states that «the attractive van der Waals forces play a dominant role in the production of the secondary maximum and minimum in the $G(r)$ of Fig. 1» (although there is only one minimum on the figure) and that «the distribution function in a fluid of rigid spheres with no attractive forces would exhibit a single maximum at $r=b$. It seems he would later change his mind on the importance of the attractive force. He also predicts that using better approximations for the interaction term would produce more maxima and minima.

He would carry on with such computations and, as is typical of good fundamental research, evolve from more general and complex cases to simpler and toy-model ones, to arrive at increasingly eerily similar shapes to ours. This is from a fairly early paper following his 1935 breakthrough, based on simple but very approximate analytical solutions:

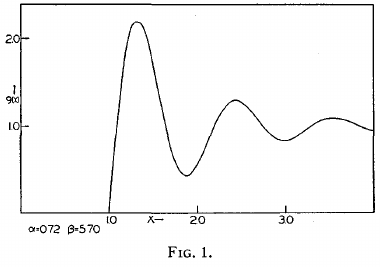
1939 computations by Kirkwood from Ref. , a neat improvement on his 1935 'sketch' above.

This is from a later (1950) text where solutions are obtained numerically:

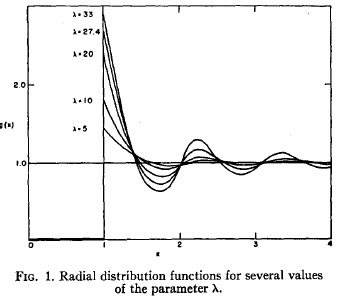
1950 computations from Ref. , now very close in appearance to our gapped coherent source, but obtained as a result of hefty calculations.

The integral equations solved «with the use of International Business Machine equipment» are still very complex. In particular, they fail to produce a solution past a density, at which point the Authors conclude that this «evidently represents the limit of stability of a fluid phase of rigid spheres. For greater densities, a crystalline phase is the stable phase.» That brings them into fascinating discussions which I suppose have been resolved since then:

At any rate, the calculations and conceptual approaches so far are all very much based on thermodynamics and statistical physics, computing the Gibbs distribution of the work function. In this context, one is typically interested in the equation of state of the system (i.e., the relation between macroscopic observables or state variables of the system, such as pressure, volume and temperature). The point is that the pair correlation function happens to be a central object for such quantities. This is recognized and highlighted in another major paper in this field, by Percus and Yevick, who implement a sort of conceptual perturbation theory. Read this:

Working with the interacting gas of point particles, they find that two-body correlation functions play a major role as, indeed, the solution to the $N$-body problem can ultimately be made to depend upon the two-body correlation, and since these correlations can be obtained from the solution, this results in a self-consistent equation (cf. Section II) known as the Percus-Yevick equation. Kirkwood relied on his so-called superposition approximation that factorizes 3-particle correlation functions in terms of 2-particle ones (Eq. (7) in Ref. ). Percus & Yevick through their independence of collective excitations could upgrade this approximation which became, and I believe, still remains one of the starting points in the theory of liquids. They considered also the gas of hard spheres (Section VIII) but to compute the virial coefficients, and left to others to turn to the pair correlation function.

This was done, in fact, solved exactly by Wertheim and Thiele for the hard spheres. Their analytical solutions are not easy of access, though, and it is largely given in symbolic form, even for particular cases such as 1D with no other form of potential than that needed to define hard spheres, or, in this 1D case, so-called "hard rods". This problem is more famous under the qualification of a Tonks gas (or Tonks-Girardeau for the quantum twist it was later given).

The first clear and explicit formulation of the result I could find in this context of 1D hard spheres with no other potential, and at about this time, is from (from Kirkwood's team) who solved it in a form that we can now fully relate to:

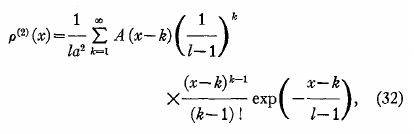
Another one, this time very concise, is from Sells et al.:
(I should check the ramifications they promise to publish later on Markov processes)

These solutions are possible because the triplet distribution function (correlations involving three particles) is, in 1D, an exact function of the doublet distributions, so Kirkwood's superposition approximation becomes exact in this case. This reminds of properties of quantum correlators that we also find to be, at the $n$th-order, simple functions of the 1st order, allowing for closure and exact solutions. This is also the reason why, it seems, the probabilities can be obtained exactly when addressing this problem from its probabilistic angle, because the particles cannot swap positions, unlike in 2D where they can move around. Note that they have a more general equation than strict hard spheres, which could be of interest for our photons.

At any rate, for hard spheres, their Eq. (8) is indeed our Eq. (4) from Ref. . So, through another route and to address a different problem, what we found out is the pair correlation function for 1D hard spheres (rods). This is not, in retrospect, surprising. What is more surprising, is that such connections were not established before, and that quantum opticians apparently did not feel the need so far to dive deeper into the nature, amount and structure of order in the photons emitted by a quantum source. If you try to do so, a large body of condensed-matter physics collapses immediately onto your shoulders, suggesting that there is much to connect between these two fields.

Moreover, if you penetrate deeper into that big forest which is the scientific literature and follow the tree of citations, you eventually find out that not only these particular results have been indeed known for a long time and remain a backbone for current research, but in fact, that they also have been entertained and obtained much earlier still and following even more straightforward models. There is a great discussion in Frenkel's 1946 Kinetic Theory of Liquids, in the Section "Dependence of the Structure of Liquids on the Free Volume". The basic picture of a 1D crystal exposed there is simple: pressure packs all the molecules, most simply described as hard spheres, together. As you increase the total length available, there is now free "volume" between the molecules, whose arrangements due to thermal motion describe melting into a liquid and ultimately into a gas. This is too simple by today's standard—and Kirkwood in particular criticized this picture very much—but it gives a reasonable initial picture. Such an arragement can be computed by probalistic methods, namely, those used by Smoluchowski to describe coagulation. A snapshot of Frenkel's calculation, actually starting with point-like spheres ("dots"), reads as follows (p°126 of the 1946 edition):

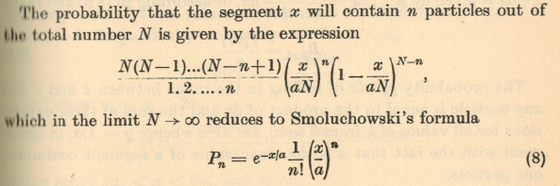
He then recovers, two pages later, our result by substitution in his configuration of a finite diameter for the spheres:

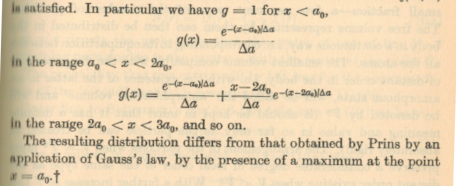
There, I am puzzled by the statements that $g(r)=1$ inside the sphere (should be zero) or the alleged disagreements with Prins who finds a maximum elsewhere.

In this discussion, Frenkel discusses a lot Kirkwood (it is interesting to read the latter's review of the book although it is nowhere as outspoken as that from Harold Neville Vazeille Temperley who, slightly frustrated not to see the problem of turbulence solved, still concedes that «it is only right to mention that the book was written in Moscow in 1942, and has suffered delay in publication» or that «In spite of the War, the book is printed on very nice paper»). But Frenkel also refers prominently to a forgotten Dutch scientist, Jan Albert Prins (who has not even a Wikipedia page), who apparently first provided the expression to compute diffracted intensities from molecular arrangements.

But even more importantly for our present discussion, in that very paper—and we are speaking of 1927—Prins (Zernike and Prins, that is) actually also discuss the 1D gas of hard spheres, with no interactions, and although I couldn't get much of their text which is written in German, it is clear that the result was obtained fully and much exploited as it was also used, so it seems, to establish the scattering-diffracted result mentioned above.

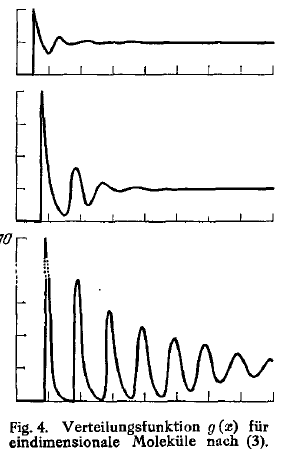
The caption translates to "Distribution function g(z) for one-dimensional molecules according to (3)" and this is (3):

Their method apparently is the one later reproduced by Frenkel in his book, based on probabilistic arguments of how to distribute N points in a line and taking a thermodynamic limit. That makes the noted departure even more confusing. Maybe he is referring to still another text. Anyway, this is therefore closer to our own approach which also relies on probabilities, but of photon-emission conditioned to the knowledge of an heralding event and without taking a thermodynamic limit:

These calculations are in contrast from those of the later results from Kirkwood and friends, culminating with Wertheim and others, that rely on complex statistical integrals instead. It is remarkable that almost a decade earlier, Prins could get from his basic model much more insightful and complete structures, including full analytical solutions that he could graph with high precision, as compared to the more elaborate but approximate models from Kirkwood that, in comparison, appear like monstrous student-like reconstructions by hand. I let you read how he describes the plotting process where he interpolates over discontinuities...

Our description also hinges on the counter-intuitive nature of the phenomenon for photons, as bunching is being observed while one is removing photons (this can also happen for coincidences, as described in the text). In this respect, it is interesting that for the condensed-matter counterpart too, this has generated debates such as why is a hard sphere gas correlated?

In conclusion, our mathematical expression has been long-time obtained through the extreme simplification of what models a liquid. This later evolved into much more sophisticated formalisms with the need to include important considerations for realistic condensed matter, starting with the dimensionality, temperature, details of the interactions, structures of the molecules, etc., to become a tenet of the theory of liquids. An attractive potential is, for instance, typically considered (think of Lennard-Jones potentials), which makes the pair-correlation function not zero inside the gap (cf. Eq. (15) in Ref. ). All these "sophistications" remain unnecessary for a photon stream, for which the main departure is that we are dealing with distribution in time rather than in space. This still brings forward interesting questions whether concepts and techniques (including results) of thermodynamic and statistical physics could shed light on photon correlations of increasingly complex types of quantum light. Could/should we speak of the entropy of the light produced by a quantum source? Should we worry about its equation of state and bring the Tonks-Girardeau physics into it? The gapped-coherent source that we introduced, with its rigid gap, remains highly idealized. The output of a dynamical system such as homodyned resonance fluorescence can resemble very much the pair-correlation function of a "more complicated variation" of the gapped coherent state, in quite the same way that 3D, interacting or even actual (experimental) pair correlation functions differ from the Zernike and Prins solution.

It is therefore possible that a fruitful and meaningful bridge has been established between photon correlations (quantum optics) and molecular arrangement (condensed matter). I will keep this in mind when revisiting known results, starting with Glauber's definition of quantum coherence; did he ever refer to those very similar concepts to characterize and set apart gases, fluids and solids when he was himself characterizing and setting apart thermal, coherent and quantum light?

Links

• Pair distribution function.
• 1-dimensional hard rods on the SklogWiki.

References

— Fabrice • 20:13, 15 July 2023