Crash Course in Scientific Computing

III. Computer Programming

Computers are good at computing! We have seen various definitions of Euler's number $e$, of which, in particular:

$$\tag{1}e=\lim_{n\rightarrow\infty}\left(1+{1\over n}\right)^n$$

$$\tag{2}e=\sum_{k=0}^\infty{1\over k !}$$

A computer would make a great job of checking this, in particular when convergence is slow. It will also allow us to deepen this important business of convergence.

Let us compute (1): for $n=1$, this is $(1+(1/1))=2$. For $n=2$, this is $(1+(1/2))^2=9/4=2.25$. For $n=3$, this is $(1+(1/3))^3=(4/3)^3=64/27=2.\overbar{370}$. Unlike computers, we get pretty tired. So we can ask the computer to do it. This is how one popular computer program, Wolfram's Mathematica, would do it:

Table[N[(1 + 1/n)^n], {n, 1, 10}]
{2., 2.25, 2.37037, 2.44141, 2.48832, 2.52163, 2.5465, 2.56578, \
2.58117, 2.59374}

It is, literally, just doing the same as we've been doing, except that it did that in 0.000041s. Does this converge to $e\approx 2.71828$? If so, very slowly. Let us check with more points:

Table[N[(1 + 1/n)^n], {n, 1, 100}]
{2., 2.25, 2.37037, 2.44141, 2.48832, 2.52163, 2.5465, 2.56578, \
2.58117, 2.59374, 2.6042, 2.61304, 2.6206, 2.62715, 2.63288, 2.63793, \
2.64241, 2.64643, 2.65003, 2.6533, 2.65626, 2.65897, 2.66145, \
2.66373, 2.66584, 2.66778, 2.66959, 2.67128, 2.67285, 2.67432, \
2.6757, 2.67699, 2.67821, 2.67936, 2.68044, 2.68146, 2.68244, \
2.68336, 2.68423, 2.68506, 2.68586, 2.68661, 2.68733, 2.68802, \
2.68868, 2.68931, 2.68992, 2.6905, 2.69105, 2.69159, 2.6921, 2.6926, \
2.69307, 2.69353, 2.69398, 2.6944, 2.69481, 2.69521, 2.6956, 2.69597, \
2.69633, 2.69668, 2.69702, 2.69734, 2.69766, 2.69797, 2.69827, \
2.69856, 2.69884, 2.69912, 2.69938, 2.69964, 2.69989, 2.70014, \
2.70038, 2.70061, 2.70084, 2.70106, 2.70127, 2.70148, 2.70169, \
2.70189, 2.70209, 2.70228, 2.70246, 2.70264, 2.70282, 2.703, 2.70317, \
2.70333, 2.7035, 2.70365, 2.70381, 2.70396, 2.70411, 2.70426, 2.7044, \
2.70454, 2.70468, 2.70481}

This time it took 0.000449s, so still fast enough, but even the 100th number doesn't get us quite there, the 2nd decimal is still off! We can get a sense of what the computer computes by plotting it. A picture is worth a hundred numbers!

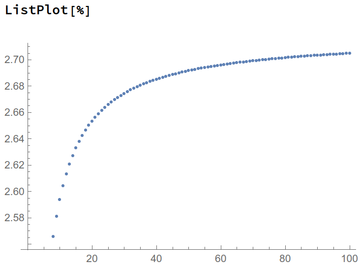
The fact that the curve still evolves (it is not horizontal), although slowly, shows that the calculation is not over. We don't have to compute all the terms though, only to take $n$ large enough, so let us see what we get with:

N[(1 + 1/1000)^1000]
2.71692

A nice computer problem: which value of $n$ do we need to take so that the displayed value, i.e., to 5 decimal places, be the correct (theoretical) value?

Ah ah! Well, the 2nd decimal is correct, but not the third. If we zoom as we compute, we see that convergence remains