m (→Gallery) |
m (→Antibunching) |
||
| Line 7: | Line 7: | ||
for all $\tau$ in a neigborhood of~$\tau=0$. Note that this allows $g^{(2)}(0)$ to be larger than unity and thus to have a super-Poissonian antibunched source, just as one can have sub-Poissonian bunched ones. The confusion (reconciliation?) with $g^{(2)}$ for typical cases is that they could be monotonic (or monotonic enough) to take the case $\tau\to\infty$ where $g^{(2)}(\infty)=1$. We discuss a bit the definition of antibunching for instance in Section~II of Ref. {{onlinecite|lopezcarreno22a}} but one could make a more thorough analysis, extending that of Zou and Mandel.{{cite|zou90a}} | for all $\tau$ in a neigborhood of~$\tau=0$. Note that this allows $g^{(2)}(0)$ to be larger than unity and thus to have a super-Poissonian antibunched source, just as one can have sub-Poissonian bunched ones. The confusion (reconciliation?) with $g^{(2)}$ for typical cases is that they could be monotonic (or monotonic enough) to take the case $\tau\to\infty$ where $g^{(2)}(\infty)=1$. We discuss a bit the definition of antibunching for instance in Section~II of Ref. {{onlinecite|lopezcarreno22a}} but one could make a more thorough analysis, extending that of Zou and Mandel.{{cite|zou90a}} | ||
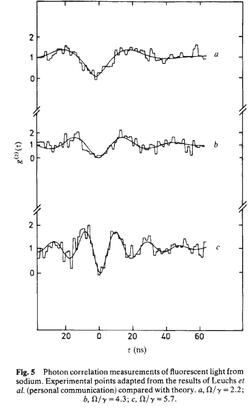
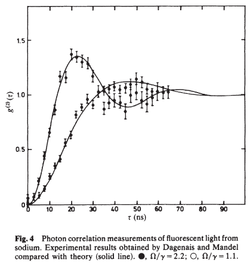
| − | The first antibunching is from Kimble{{etal}}{{cite|kimble77a}} | + | The first antibunching is from Kimble{{etal}},{{cite|kimble77a}} although according to [[Walls]],{{cite|walls79a}} this was also simultaneously reported by [[Leuchs]]{{etal}} who did not publish their findings, but that Walls provides in his review (along with, interestingly, much better results than the ones published by Kimble{{etal}} in their text): |
| + | |||
| + | <center><wz tip="Antibunching by Leuchs et al, unpublished! but reported by Walls.">[[File:Screenshot_20240218_173113.png|250px]]</wz><wz tip="Antibunching by Dagenais and Mandel (without Kimble) and also as reported by Walls, much better than the one they published (with Kimble).">[[File:Screenshot_20240218_173157.png|250px]]</wz></center> | ||
== Gallery == | == Gallery == | ||
Revision as of 16:34, 18 February 2024
Contents |
Antibunching
Antibunching is the tendency of photons to repulse each other in time, i.e., to be less likely to be found together than later apart in time. At such, this is a particular case of photon statistics, as measured by the so-called $g^{(2)}$. But this is a case of great importance as it signals, or is usually linked, to the quantum rgime. Unfortunately, there have been several differing definitions, based around the idea that antibunching describes single-photons, or suppression of two-photon (or multiphoton) coincidence. In particular, various authors (ourselves included, when convenient) understand antibunching as the condition $g^{(2)}(0)\approx 0$ (or even equal to zero, or less than unity). There is no good term that I know for the latter condition (some speak of "purity", which I also don't like very much; a better term would be sub-Poissonian but that's awkward). A more accurate, widespread, agreed-upon definition of antibunching itself is:
$$g^{(2)}(0)< g^{(2)}(\tau)$$
for all $\tau$ in a neigborhood of~$\tau=0$. Note that this allows $g^{(2)}(0)$ to be larger than unity and thus to have a super-Poissonian antibunched source, just as one can have sub-Poissonian bunched ones. The confusion (reconciliation?) with $g^{(2)}$ for typical cases is that they could be monotonic (or monotonic enough) to take the case $\tau\to\infty$ where $g^{(2)}(\infty)=1$. We discuss a bit the definition of antibunching for instance in Section~II of Ref. [1] but one could make a more thorough analysis, extending that of Zou and Mandel.[2]
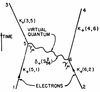
The first antibunching is from Kimble et al.,[3] although according to Walls,[4] this was also simultaneously reported by Leuchs et al. who did not publish their findings, but that Walls provides in his review (along with, interestingly, much better results than the ones published by Kimble et al. in their text):
Gallery
Here follows a collection of antibunching traces $g^{(2)}(\tau)$. It is of course impossible to be comprehensive, but hopefully this will grow to be representative enough of everything and everybody:
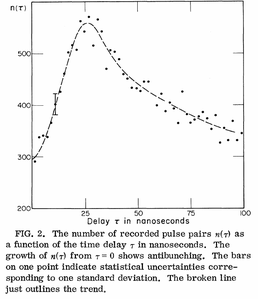
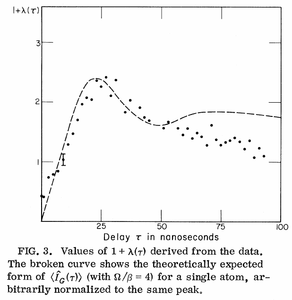
From Kimble et al.[3]
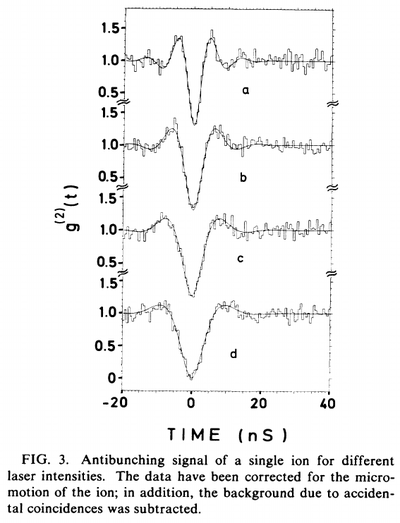
From Diedrich et al.[5]
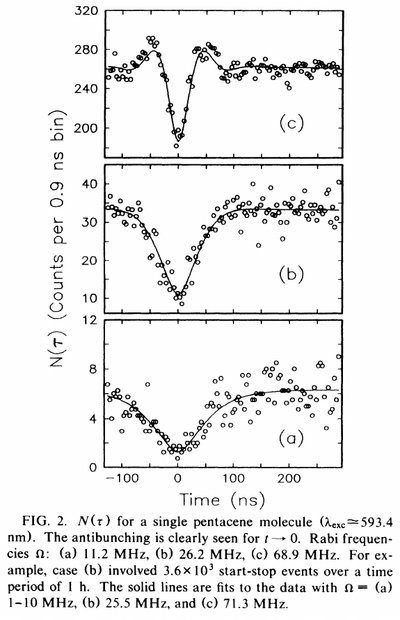
From Basché et al.[6]
From Ambrose et al.[7]
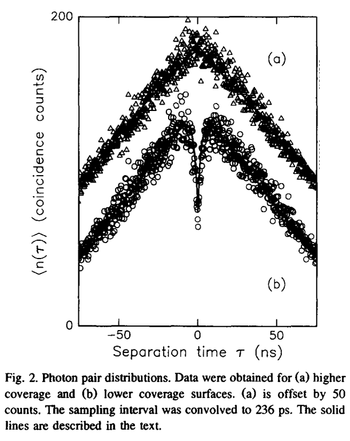
They consider histograms of time-difference so with no normalization of their signal back to unity at long time delays. The identity of this histogram method with a complete~$g^{(2)}$ is valid only over times much smaller than the mean time between detections.[8]
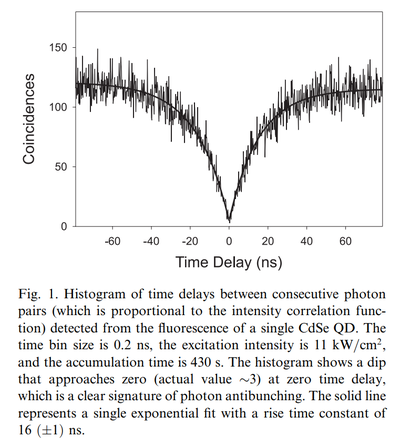
From Lounis et al.[9]
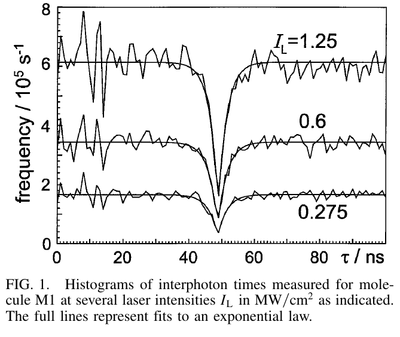
From Fleury et al.[10]
From Kurtsiefer et al.[11]
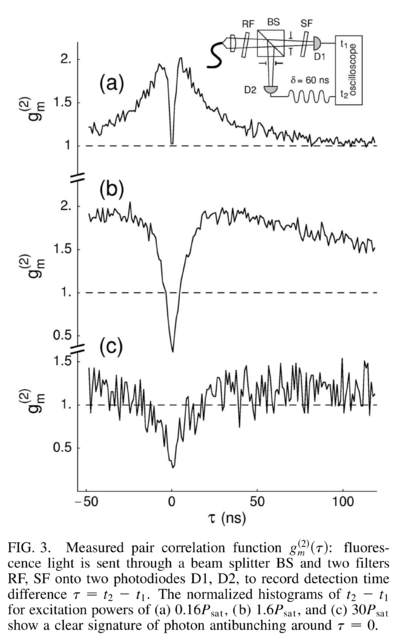
The bunching elbows are accounted here for the first time with a rate-equation model (yielding a bi-exponential curve).
From Michler et al.[12]
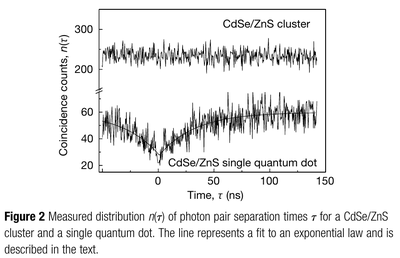
From Zwiller et al.[13]
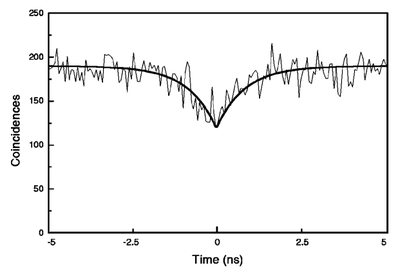
From Messin et al.[14]
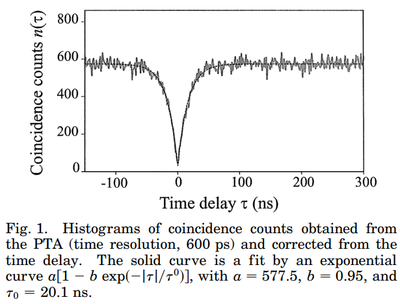
From Hübner et al.[15]
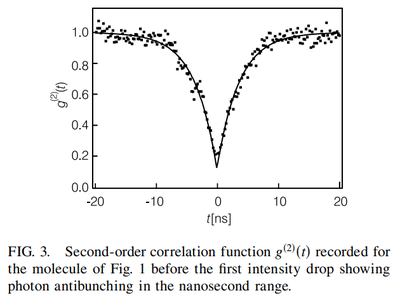
From Ampem-Lassen et al.[16]
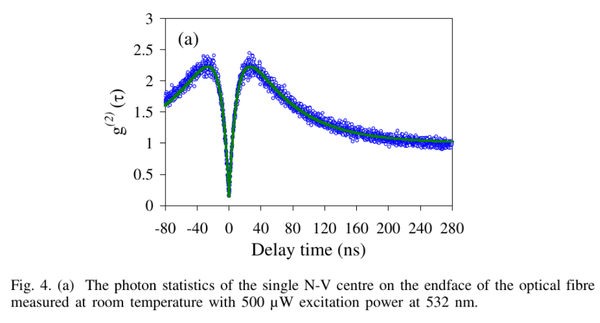
From Neu et al.[17]
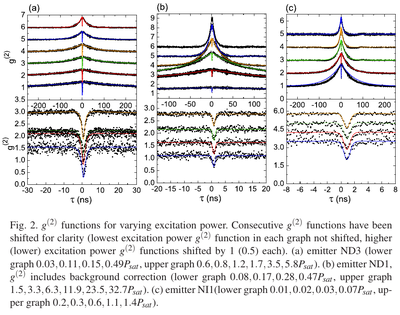
From Nothaft et al.[18]
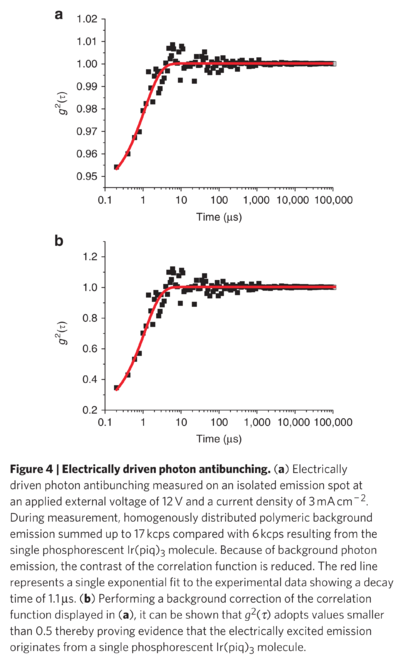
Top: raw-data; Bottom: with correction. But their optical pumping provides antibunching similar to the "corrected" electrically-pumped one. This is a log-linear plot, the red line is actually a single exponential.
From Davanço et al.[19]
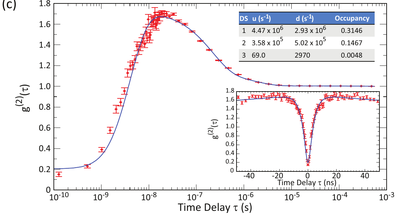
From Berthel et al.[20]
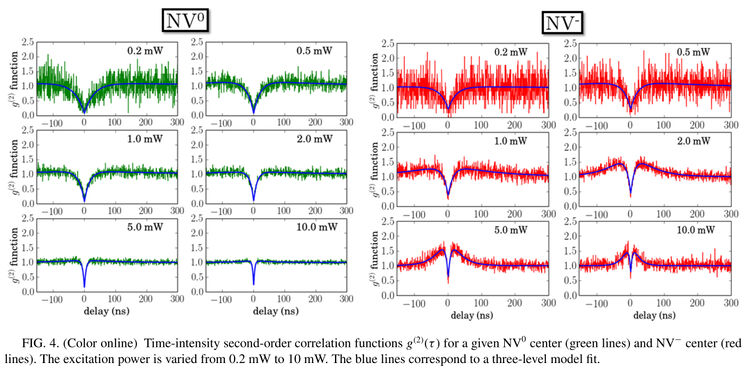
From Koperski et al.[21]
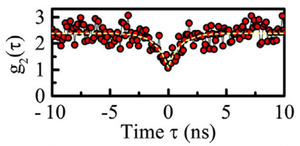
From Wang et al.[22]
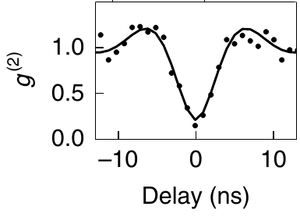
From Boll et al.[23]
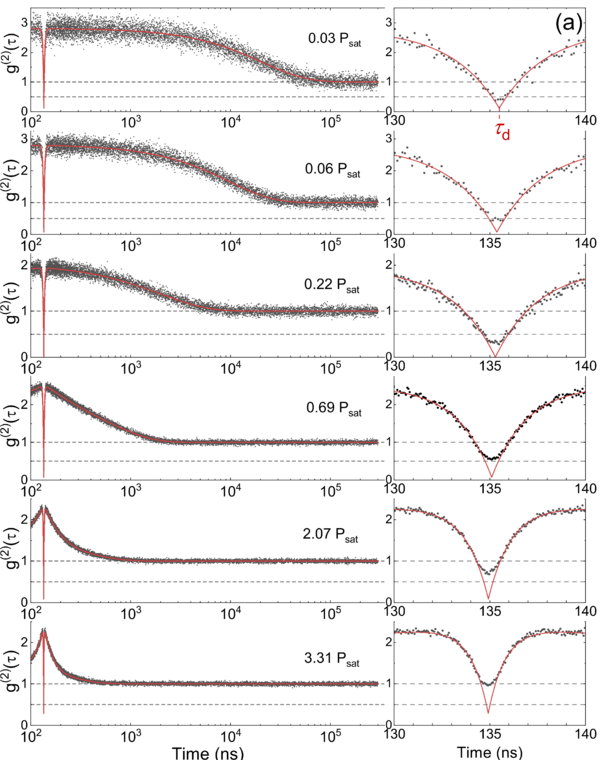
From Nahra et al.[24]
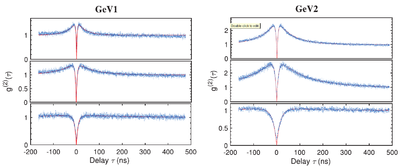
From Fiedler et al.[25]
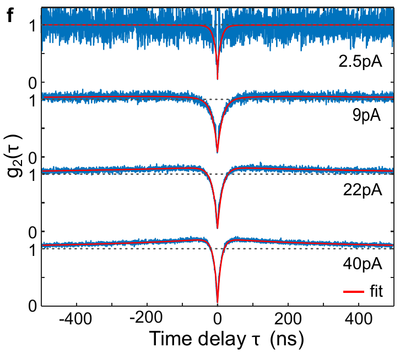
The 'photon bunching at non-zero correlation times' is still attributed to a metastable (shelving) state, like in the original paper.[11]
Transitions between various types statistics
Something which frequency-filtering does very neatly.
- Transition from Antibunching to Bunching in Cavity QED. M. Hennrich, A. Kuhn and G. Rempe in Phys. Rev. Lett. 94:053604 (2005).
- Light of Two Atoms in Free Space: Bunching or Antibunching?. S. Wolf, S. Richter, J. v. Zanthier and F. Schmidt-Kaler in Phys. Rev. Lett. 124:063603 (2020).
- Sub-to-super-Poissonian photon statistics in cathodoluminescence of color center ensembles in isolated diamond crystals. S. Fiedler, S. Morozov, D. Komisar, E. A. Ekimov, L. F. Kulikova, V. A. Davydov, V. N. Agafonov, S. Kumar, C. Wolff, S. I. Bozhevolnyi and N. A. Mortensen in Nanophot. 12:2231 (2023).
Links
- https://physics.stackexchange.com/questions/623095/how-can-sub-and-super-poissonian-statistics-be-distinguished-from-bunching-and
- https://physics.stackexchange.com/questions/633044/is-anti-bunched-light-necessarily-sub-poissonian
References
- ↑ Loss of antibunching. J. C. López Carreño, E. Zubizarreta Casalengua, B. Silva, E. del Valle and F. P. Laussy in Phys. Rev. A 105:023724 (2022).
- ↑ Photon-antibunching and sub-Poissonian photon statistics. X. T. Zou and L. Mandel in Phys. Rev. A 41:475 (1990).
- ↑ 3.0 3.1 Photon Antibunching in Resonance Fluorescence. H. J. Kimble, M. Dagenais and L. Mandel in Phys. Rev. Lett. 39:691 (1977).
- ↑ Evidence for the quantum nature of light. D. F. Walls in Nature 280:451 (1979).
- ↑ Nonclassical radiation of a single stored ion. F. Diedrich and H. Walther in Phys. Rev. Lett. 58:203 (1987).
- ↑ Photon antibunching in the fluorescence of a single dye molecule trapped in a solid. T. Basché, W. E. Moerner, M. Orrit and H. Talon in Phys. Rev. Lett. 69:1516 (1992).
- ↑ Fluorescence photon antibunching from single molecules on a surface. W. P. Ambrose, P. M. Goodwin, J. Enderlein, D. J. Semin, J. C. Martin and R. A. Keller in Chem. Phys. Lett. 269:365 (1997).
- ↑ La fluorescence de résonance: étude par la méthode de l'atome habillé. S. Reynaud in Annales de Physique 8:351 (1983).
- ↑ Photon antibunching in single CdSe/ZnS quantum dot fluorescence. B. Lounis, H. Bechtel, D. Gerion, P. Alivisatos and W. Moerner in Chem. Phys. Lett. 329:399 (2000).
- ↑ Nonclassical Photon Statistics in Single-Molecule Fluorescence at Room Temperature. L. Fleury, J. Segura, G. Zumofen, B. Hecht and U. P. Wild in Phys. Rev. Lett. 84:1148 (2000).
- ↑ 11.0 11.1 Stable Solid-State Source of Single Photons. C. Kurtsiefer, S. Mayer, P. Zarda and H. Weinfurter in Phys. Rev. Lett. 85:290 (2000).
- ↑ Quantum correlation among photons from a single quantum dot at room temperature. P. Michler, A. İmamoğlu, M. D. Mason, P. J. Carson, G. F. Strouse and S. K. Buratto in Nature 406:968 (2000).
- ↑ Single quantum dots emit single photons at a time: Antibunching experiments. V. Zwiller, H. Blom, P. Jonsson, N. Panev, S. Jeppesen, T. Tsegaye, E. Goobar, M. Pistol, L. Samuelson and G. Björk in Appl. Phys. Lett. 78:2476 (2001).
- ↑ Bunching and antibunching in the fluorescence of semiconductor nanocrystals. G. Messin, J. P. Hermier, E. Giacobino, P. Desbiolles and M. Dahan in Opt. Lett. 23:1891 (2001).
- ↑ Photon Antibunching and Collective Effects in the Fluorescence of Single Bichromophoric Molecules. C. G. Hübner, G. Zumofen, A. Renn, A. Herrmann, K. Müllen and T. Basché in Phys. Rev. Lett. 91:093903 (2003).
- ↑ Nano-manipulation of diamond-based single photon sources. E. Ampem-Lassen, D. A. Simpson, B. C. Gibson, S. Trpkovski, F. M. Hossain, S. T. Huntington, K. Ganesan, L. C. L. Hollenberg and S. Prawer in Opt. Express 17:11287 (2009).
- ↑ Photophysics of single silicon vacancy centers in diamond: implications for single photon emission. E. Neu, M. Agio and C. Becher in Opt. Express 20:19956 (2012).
- ↑ Electrically driven photon antibunching from a single molecule at room temperature. M. Nothaft, S. Höhla, F. Jelezko, N. Frühauf, J. Pflaum and J. Wrachtrup in Nature Comm. 3:628 (2012).
- ↑ Multiple time scale blinking in InAs quantum dot single-photon sources. M. Davanço, C. S. Hellberg, S. Ates, A. Badolato and K. Srinivasan in Phys. Rev. B 89:161303 (2014).
- ↑ Photophysics of single nitrogen-vacancy centers in diamond nanocrystals. M. Berthel, O. Mollet, G. Dantelle, T. Gacoin, S. Huant and A. Drezet in Phys. Rev. B 91:035308 (2015).
- ↑ Single photon emitters in boron nitride: More than a supplementary material. M. Koperski, K. Nogajewski and M. Potemski in Opt. Commun. 411:158 (2018).
- ↑ Turning a molecule into a coherent two-level quantum system . D. Wang, H. Kelkar, D. Martin-Cano, D. Rattenbacher, A. Shkarin, T. Utikal, S. Götzinger and V. Sandoghdar in Nature Phys. 15:483 (2019).
- ↑ Photophysics of quantum emitters in hexagonal boron-nitride nano-flakes. M. K. Boll, I. P. Radko, A. Huck and U. L. Andersen in Opt. Express 28:7475 (2020).
- ↑ Single germanium vacancy centers in nanodiamonds with bulk-like spectral stability. M. Nahra, D. Alshamaa, R. Deturche, V. Davydov, L. Kulikova, V. Agafonov and C. Couteau in AVS Quantum Sci. 3:012001 (2021).
- ↑ Sub-to-super-Poissonian photon statistics in cathodoluminescence of color center ensembles in isolated diamond crystals. S. Fiedler, S. Morozov, D. Komisar, E. A. Ekimov, L. F. Kulikova, V. A. Davydov, V. N. Agafonov, S. Kumar, C. Wolff, S. I. Bozhevolnyi and N. A. Mortensen in Nanophot. 12:2231 (2023).
| |||||||||||||