Contents |
Quantum physics
Quantum mechanics occupies a very unusual place among physical theories: it contains classical mechanics as a limiting case, yet at the same time it requires this limiting case for its own formulation—Landau & Lifshitz, Quantum Mechanics: Non-Relativistic Theory.
Historical developments
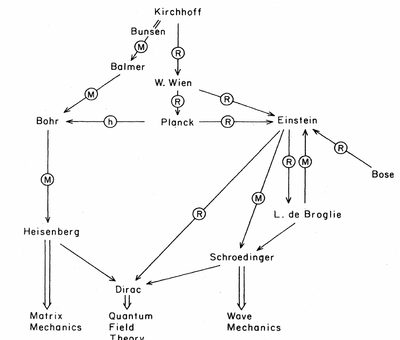
One could name Planck as the grandfather of quantum theory, first because he looks like one, second because he indeed made the first postulate of quantization to explain blackbody radiation. The fundamental quantum constant $h$ is also named after him.
Although Einstein has been very critical of quantum mechanics—in particular disregarding it for his theory of everything which is how he got disconnected from mainstream physics—he has been involved very closely to its early developments.[1]
The father of the "Old Quantum Mechanics" was Bohr with his breakthrough in accounting for the stability of atoms with his eponymous model. He also seeded the idea of "quantum jump" and, of course, championed the still-leading Copenhagen interpretation. The modern version was fathered by Heiseinberg (matrix mechanics) and Schrödinger (wave mechanics). This is from the formalism point of view, the first conceptual leap was made by Born who introduced the probabilistic interpretation to the wavefunction, in sharp contrast to Schrödinger who was thinking of it as a real, physical undulatory wave of matter (following de Broglie's pioneering concept), which is untenable for multi-particles and led to the horrific (at least to Schrödinger) notion of entanglement.
Schrödinger equation
The pillar of quantum theory is Schrödinger's equation:
$$i\hbar\partial_t\psi=H\psi$$
with $H$ the Hamiltonian and $\psi$ the wavefunction. What the wavefunction is is the problem of interpretation of quantum mechanics. But as the name suggests, it is at least a "wave" of some sort and quantum mechanics for a while was known as "wave mechanics". The seed of the idea came from de Broglie, in fact Weyl in the 2nd edition of his Gruppentheorie und Quantenmechanik named Schrödinger's equation the "de Broglie equation", something to which Schrödinger personally objected to in a letter, observing in passing not only he was the true father but that he was also the father of the Klein-Gordon equation but did not object to that «because this is very convenient as a disctinction».[2] In fact, de Broglie had also toyed with the Klein-Gordon equation as the possible wave equation for $\psi$. Among the many objections of de Broglie to the Schrödinger equation was his non-relativistic character. Schrödinger on the other hand did not publish his Klein-Gordon equation because it did not provide the good fine structure, but there are traces of his antecedence. Schrödinger is, indeed, the true and proper father of his eponymous equation.
Klein-Gordon equation
The Klein-Gordon was the first equation for $\psi$ to be developed, the one purposedly kept under silence by Schrödinger because it was not compatible with Born's interpretation, and sentenced to death by Pauli who could show the equivalence between the Heisenberg (matrix) approach and the wave (Schrödinger) approach but not with the KG version. It reads:
$$\left({\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}-\nabla ^{2}\right)\psi=-{\frac {m^{2}c^{2}}{\hbar ^{2}}}\psi\,.$$
It is, however, a valid equation, and was indeed the first (but not the most important, see Dirac equation) relativistic wave equation. Oskar Klein was the first to publish it (Schrödinger the first to obtain it, although Klein later observed he had his equation even before Schrödinger's, which is contained as a particular case[2]). The KG equation was not the highlight of Klein's paper, who was instead seeking a five-dimensional theory unifying quanta and relativity:
I never thought that that was any important thing, just to have the relativistic scalar equation after Schrödinger's equation.—Oskar Klein on the Klein-Gordon equation, Ref. 14 in Ref. [2]
The equation was also entertained by Walter Gordon, who maybe because he was one of the few to take it seriously, got it named after him, although his work came after the equation had been written and rediscovered many times (in addition to Schrödinger and Klein, also by Fock, Heisenberg, Pauli, etc.) Gordon did not, however, restore the equation to the important place it now occupies. This had to go through Dirac's equation first. Relativistic quantum mechanics calls for an entire field altogether, known as quantum field theory. In this context, the KG equation indeed ranks among the fundamental equations for elementary particles, namely, spinless massive bosons, such as mesons. Interestingly, Pauli himself later regarded his work (with Weisskopf) based on the KG equation as the anti-Dirac paper, having thus pushed this equation too much in its extremities (invalid or the correct quantum-field theoretic electron equation).
Dirac equation
The Dirac equation achieves what the Klein-Gordon failed to do, provide an accurate theoretical description for the relativistic electron, in particular its spin properties. Its main departure and breakthrough is to remain first-order in time, like the non-relativistic (Schrödinger) equation. It reads:
$$i\hbar\gamma^\mu\partial_\mu\psi=mc\psi\,.$$
People
Besides those who made the History of the field (see the historical developments above), interesting people on this topic include:
Further topics
This is a list of pages on that topic that you can find on this website.
- Interpretations of Quantum Mechanics — understanding what it says (you should be shocked if you do).
- Liouvillian theory — an introduction to quantum physics with dissipation.
- Bose algebra — useful identities if you're into that business.