<span class="mw-page-title-main">Polariton</span>
Fabrice P. Laussy's Web

Polariton

A polariton can be seen as a molecule of light and matter. Much like an atom binds an electron to a nucleus, a polariton binds a photon (a particle of light) to an exciton (a particle of matter).[1] Such a bonding is made possible by confining both excitations in a cavity, where they are both trapped and therefore compelled to interact. Without the cavity, which consists in two mirrors facing each others, the photon would simply fly away. But the mirrors make the photons bounce back and forth, hitting the crystal in the process and once in a while creating an excitation—that's our exciton—as the photon gets absorbed. The exciton is unstable, like a positron (it is in fact a bound electron-hole pair), an after a while, recombines to create another photon. The process repeats itself, for as long as the photon stays in the cavity. According to Quantum Mechanics, this generates a quantum superposition of the two possible states, just like the Schrödinger cat, but instead of being alive and dead simultaneously, the particle is light and matter simultaneously:

$$\ket{\mathrm{photon}}+\ket{\mathrm{exciton}}$$

These half-light/half-matter particles have fantastic properties, which they inherit from their underlying components:

  • Polaritons are extremely coherent, like light.
  • Polaritons interact strongly, like matter.

They have a mass, like matter, but a very light-one (the photon has none in vacuum and a small effective one when confined in a cavity).

Their dynamics consist of characteristic Rabi oscillations.[2] In presence of a weak nonlinearity, this turns into the problem of Josephson oscillations.[3]

The concept was first proposed theoretically, and christened so, by John Hopfield[4], and its most fruitful implementation, in 2D, was discovered experimentally during a sabbatical stay in Arakawa's group in Tokyo by Claude Weisbuch,[5] who referred to it as his «Japanese effect.»[6] Weisbuch did not initially recognized it as a Hopfield polariton, or "bulk polariton", for which the photon is delocalized in the full 3D crystal, but as a cavity QED effect (Weisbuch was in fact already a polariton expert, having reported its first resonant observation 15 years earlier[7]). The situation was quickly settled during the July (1993) Erice Summer School on "Confined Electrons and Photons: New Physics and Applications" which featured «heated sessions (involving in particular the two Elis, Eli Burstein and Eli Yablonovitch) on the nature of these excitations» according to Weisbuch himself.[8] The name of "Cavity-Polariton" was then agreed to well describe Hopfield's counterpart in reduced dimensionality, and be more suitable than Weisbuch's initial choice for merly Rabi splitting:

The term "vacuum field Rabi splitting" has so far been used for semiconductor microcavities in analogy to atomic physics where this effect was first observed. From a solid state physics point of view, where dispersion has to be considered, the term "cavity-polariton" is more appropriate.

— R. Houdré, R.P. Stanley and U. Oesterle, 🕮Confined Electrons and Photons: New Physics and Applications. Claude Weisbuch and Elias Burstein (Editors). Springer, 1995. [ISBN: 978-1-4613-5807-7]

The first appearance of the "cavity polariton" term was in Ref. [9], where the idea of the underlying dispersion was being formed. The breakthrough came in Ref. [10] where the now famous polariton dispersion was provided for the first time:

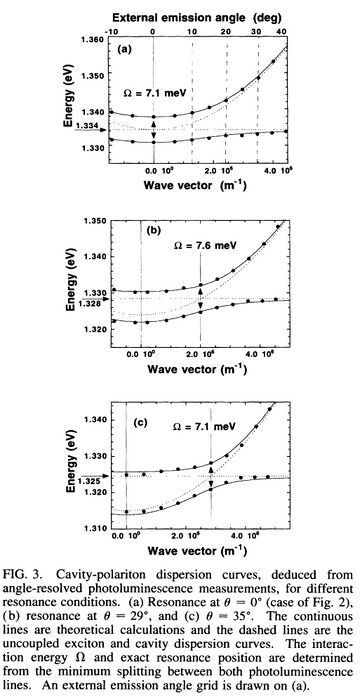
It seems that the theorists who should have predicted cavity-polaritons are C. Andreani et al.,[11] who narrowly missed it by overlooking the dimensionality mismatch could be fixed with a cavity. He seems, however, to have readily understood (and explained) it[12] to R. Houdré et al. as they were shaping the field.[6]

Concepts

Important concepts (I'm particularly interested in) include:

To do

A historical review of the polariton concept, from Hopfield's lone-warrior paper[4] that gets all the credit despite fairly serious variations with the finally adopted results (including in its operational definition, involving four operators), along with other contributions.[13][14]

Literature

The topic is covered at depth in our book Microcavities. Reviews include [15][16][17][18].

Historical overviews includes Refs. [19][6], etc.

Links

References

  1. ↑ Excitons in crystals. F. P. Laussy and A. Kavokin in Encycl. Cond. Mat. Phys. 3:706 (2024). 
  2. ↑ Ultrafast Control and Rabi Oscillations of Polaritons. L. Dominici, D. Colas, S. Donati, J. P. Restrepo Cuartas, M. De Giorgi, D. Ballarini, G. Guirales, J. C. López Carreño, A. Bramati, G. Gigli, E. del Valle, F. P. Laussy and D. Sanvitto in Phys. Rev. Lett. 113:226401 (2014).
  3. ↑ Polaritonic Rabi and Josephson oscillations. A. Rahmani and F.P. Laussy in Sci. Rep. 6:28930 (2016). 
  4. ↑ 4.0 4.1 Theory of the Contribution of Excitons to the Complex Dielectric Constant of Crystals. J. J. Hopfield in Phys. Rev. 112:1555 (1958).
  5. ↑ Observation of the coupled exciton-photon mode splitting in a semiconductor quantum microcavity. C. Weisbuch, M. Nishioka, A. Ishikawa and Y. Arakawa in Phys. Rev. Lett. 69:3314 (1992).
  6. ↑ 6.0 6.1 6.2 Early stages of continuous wave experiments on cavity-polaritons. R. Houdré in Phys. Stat. Sol. B 242:2167 (2005).
  7. ↑ Resonant Polariton Fluorescence in Gallium Arsenide. C. Weisbuch and R. G. Ulbrich in Phys. Rev. Lett. 39:654 (1977).
  8. ↑ Microcavities in École Polytechnique Fédérale de Lausanne, École Polytechnique (France) and elsewhere: past, present and future. C. Weisbuch and H. Benisty in Phys. Stat. Sol. B 242:2345 (2005).
  9. ↑ Room-temperature cavity polaritons in a semiconductor microcavity. R. Houdré, R. P. Stanley, U. Oesterle, M. Ilegems and C. Weisbuch in Phys. Rev. B 49:16761 (1994).
  10. ↑ Template:Houdre04a
  11. ↑ Radiative lifetime of free excitons in quantum wells. L. C. Andreani, F. Tassone and F. Bassani in Solid State Commun. 77:641 (1991).
  12. ↑ Optical transitions, excitons and polaritons in bulk and low-dimensional semiconductor structures. L. C. Andreani in 🕮Confined Electrons and Photons: New Physics and Applications. Claude Weisbuch and Elias Burstein (Editors). Springer, 1995. [ISBN: 978-1-4613-5807-7].
  13. ↑ On the interaction between the radiation field and ionic crystals. K. Huang in Proc. R. Soc. Lond. A 208:352 (1951).
  14. ↑ Theory of electromagnetic waves in a crystal in which excitons arise. S. I. Pekar in J. Exp. Th. Phys. [ 33:1022] (1957).
  15. ↑ Template:Skolnick02a
  16. ↑ Polariton panorama. D. N. Basov, A. Asenjo-Garcia, P. J. Schuck, X. Zhu and A. Rubio in Nanophot. 10:549 (2020).
  17. ↑ Microcavity exciton polaritons at room temperature. S. Ghosh, R. Su, J. Zhao, A. Fieramosca, J. Wu, T. Li, Q. Zhang, F. Li, Z. Chen, T. Liew, D. Sanvitto and Q. Xiong in Photonics Insights 1: (2022).
  18. ↑ Coherent phenomena in exciton-polariton systems. F. Toffoletti and E. Collini in J. Phys. Mater. 8:022002 (2025).
  19. ↑ Microcavities in École Polytechnique Fédérale de Lausanne, École Polytechnique (France) and elsewhere: past, present and future. C. Weisbuch and H. Benisty in Phys. Stat. Sol. B 242:2345 (2005).