«it was understood that the so-called

vacuum field Rabi splitting effect was more complex in semiconductors than in atomic physics»

Early stages of continuous wave experiments on cavity-polaritons. R. Houdré in Phys. Stat. Sol. B 242:2167 (2005).  What the paper says!?

This is an account of the «Early stages of continuous wave experiments on cavity-polaritons» for a symposium held in honour of Marc Ilegems, with a nice overview of «most of the “easy” and straightforward effects» and providing, overall, «short history of the early stages of the cavity-polaritons»:

The aim of this paper is to highlight the historical context of the early stages of the continuous wave experiments performed on cavity-polariton with M. Ilegems during the period 1992–2000. The other key

players of this work were C. Weisbuch, R. P. Stanley and U. Oesterle.

It documents the "passing of the torch" from Claude Weisbuch to the EPFL team:

C. Weisbuch, with whom we had very close collaboration and who used to spend week (and weekend) long visits in our group, convinced us to work on what he

familiarly used to call his “Japanese effect” he had recently observed.

In another paper in the same volume, Savona also reports how Weisbuch was the first to evoke the possibility of their condensation.

Interesting excerpts include, the perception of what could be done with polaritons (connection to the thresholdless laser):

First practical application that was sought was an exciton emitter at room temperature oriented toward the once fashionable threshold-less laser [4, 5, 14, 15]. This idea was indeed described in one of the

workpart of the Esprit European program named SMILES.

The claim where the term cavity-polariton was first used in print:

The term cavity-polariton was used for the first time in 1993–1994 in [17] where some remarks implied the claim for the existence of an underlying cavity-polariton dispersion curve resulting from the anti-

crossing behaviour between the exciton and Fabry–Pérot cavity dispersion curves.

Their Ref. 17 is Ref. .

An interesting account of their difficulty in initially understanding the dispersion and how to retrieve it with angle-resolved spectroscopy:

It became apparent that we were measuring this dispersion curve when performing angle resolved photoluminescence, but the question why we were measuring it in this case whilst we knew this was never the case for bulk exci- ton-polariton or exciton in a quantum well, eluded us for a while, although explanation was just in a couple of drawing (thanks to discussions with D. Citrin and L. C. Andreani). However at this time, the field was quite small and sedate and angle resolved measurements lied in a drawer, not-understood for

more than a year.

As well as:

the single atomic picture of two coupled levels applies here although we are dealing with a pair of two-dimensional continuum systems. For a given k, a single photon mode and the single coupled exciton interact with an equivalent oscillator strength of about $10^{12}$

atoms [18].

This bring them to their detailed discussion of the transfer of internal properties to the outside by angle-resolved spectroscopy for various cases (although low-res image):

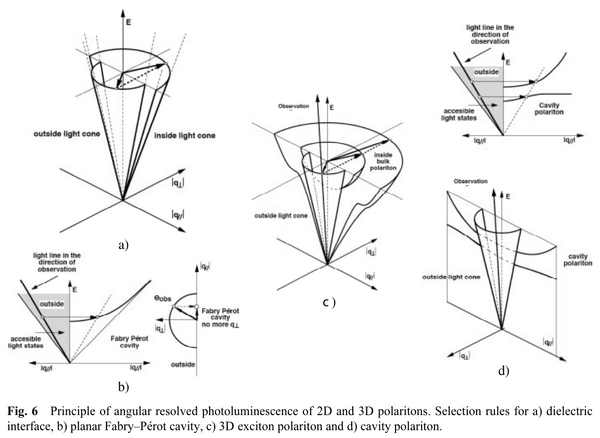
Further details on the atmosphere at the Cargèse school:

It has a nice description of the problem of how to "observe" or "evidence" strong-coupling from various observables:

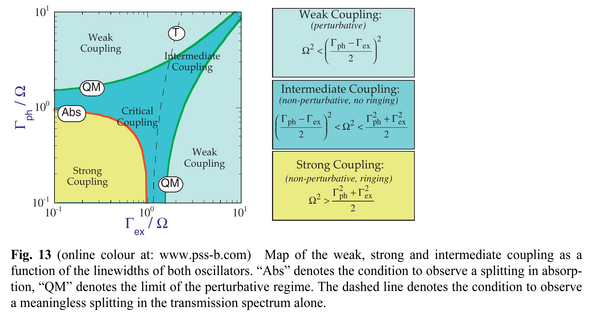
A relevant physical parameter that can be used as experimental evidence of vacuum field Rabi splitting is absorption (i.e. the dielectric susceptibility) [10], neither reflectivity nor transmission are unambiguous parameters [11]. The existence of two split levels in the cavity + atom system is evidenced by transitions that can occur at these energies. Existence of a structure in reflectivity does not make the distinction between absorption and a change in the reflectivity/transmission balance (see below). This important

point is, even now, often forgotten and led to repetitive erroneous claim by newcomers in the field.

There is a discussion on the quantum nature of polaritons in Sec. «6.5 Test of linear dispersion theory (1997)», based on single-particle observables, namely, whether polaritonic effects can manifest in the exciton-disorder light coupling.

if a quantum mechanical description of cavity-polariton was often used, this was because it provided easier to handle conceptual pictures.

The Authors come to the conclusion that

This certainly does not imply that quantum effects do not exist in cavity-polariton but that they have to be searched in more elaborated

experiments.

This is as expected but a better understanding of why they would have expected quantum effects there, and which/how, should be better understood.

There are nice coverages of effects such as "cavity pulling" (more emission from the cavity at detuning making polaritons photon-like) or of «7. Rayleigh scattering (2000)», of inhomogenous broadening (motional broadning), etc.