Leapfrog

Leapfrog ( saute-mouton) is a children's game that involves two great activities for people of all age: you jump over someone and you are being jumped over. This iterative character of an action where one is alternatively active and passive makes this simple game an inspirational metaphor for several other processes that intertwine something (such as the leapfrog algorithm).

In our case, we used the terminology to describe the "leapfrog" process in the relaxation dynamics of a quantum system. When a photon jumps from one energy level to another which is not the one immediately contiguous, it can do so by involving a virtual photon. You can picture this jumping over the intermediate energy level as a photon-aided leapfrogging, jumping with the aid of something dynamical and of its own kind, rather than relying on something static and fixed (a fence for children or a quantum state for a photon).

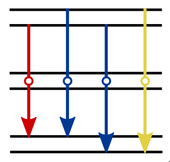
The photon is virtual because it can have an energy which does not belong to the energy level structure of the system. This produces strongly quantum correlated two-photon states as when these two photons are emitted, they become real but retain the strong connection from the way they have been generated: in a joint-leapfrogging scenario. They do not have to be degenerate and as the virtual photon can relax the conservation of energy condition $E_1-E_2=h\nu$, this produces a continuum of frequencies $\nu$ rather than the typical discrete (quantized) emission given by the difference of energies $E_i$.

You do not see leapfrog emission directly in normal spectroscopy since this is a weak process (unless under particular conditions, such as from the emission of planetary nebulae) but you can see it clearly in quantum spectroscopy where you detect photons together and pay attention to their correlations.^[1] We introduced the notion of two-photon spectrum^[2]^[3] that correlates photons of all possible frequencies. This reveals leapfrog emission as clear antidiagonal lines. For instance, in the case of the Mollow energy levels above, just as one-photon transitions yield the celebrated Mollow triplet (with the central peak twice as high because there are two possible transitions), the two-photon leapfrog transitions yield a triplet of continuous lines in the two-photon spectrum:

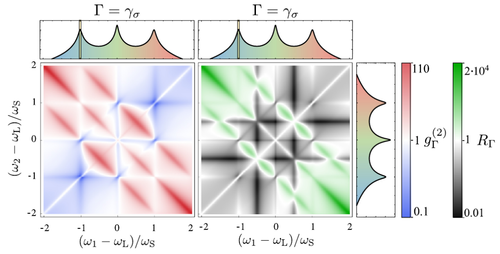
Two-photon correlation spectra computed by Sanchez Muñoz et al. (PRA 2014) for resonance fluorescence. This shows two-photon correlations $g^{(2)}_\Gamma$ (blue-red) and violation of Cauchy-Schwarz equalities $R_\Gamma$. The leapfrog emission is neatly resolved as three antidiagonal lines. Red corresponds to photon bunching (coming together, as expected for leapfrogging) and green correspond to non-classical character of the light. This shows that leapfrog photons are the chief carrier of non-classical emission.

Note that the lines are broken in some places. This happens precisely when the virtual photon of the leapfrog transition meets an energy state, which thus turns it into a real photon, so instead of a leapfrog transition, one has a cascade between two photons that successively make conventional one-photon transitions instead. This spoils their quantum correlations.

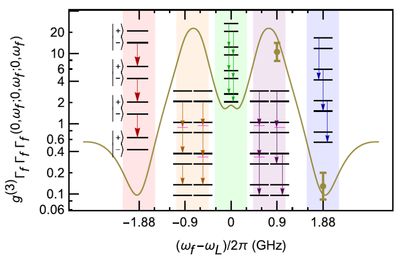
While we have theoretically predicted the leapfrog processes, their discovery in the real world belongs to the group of Andreas Muller, from the University of South Florida, who pioneered and is the current leader of experimental leapfrog physics. In a heroic experiment^[4], they manage to span over all the frequencies of emission from a strongly-driven quantum dot to systematically compute their cross-correlations and reconstruct the two-photon spectrum. This is what the theory^[5] expects for their system (left) and what they measured (right):

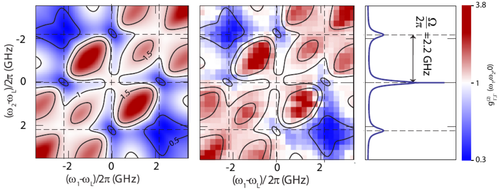
For some reason, they took a convention for axes such that leapfrog emission is diagonal (rather than antidiagonal for us). Also, for their filtering linewidths, the break-up of the lines is stronger than for our theoretical case, but still the leapfrog pattern is clear and in any case the agreement with the theory is spectacular (one is dealing with a complex solid-state system here as the implementation of the theoretical two-level system). This thus represents a fantastic scientific breakthrough, which, unfortunately for the Physical Review Letter, was recognized as such neither by the editor of the time nor one of their Referees (this was published in Phys. Rev. B instead^[4]). This is a sure mark of success when something is so disruptive that people feel cautious about letting it be published in the appropriate journal.

Leapfrog processes will clearly play an increasing role in quantum optics, especially as multi-photon physics grows mature. The clock is ticking to see how many years ahead of time the Muller group will be on the rest of the world, with many still even unaware of its existence and little frenzy to reproduce the South Florida results and extend them or bring them towards applications. So far, only the surface of the problem has been scratched and many developments, both at a fundamental or applied level, are in sight.

To start with, there is a clear extension of the concept to arbitrary $N$-photon transitions, jumping from one energy level to another involving $N-1$ virtual photons. This shows 3-photon leapfrogs in the Mollow ladder (left) as well as a combination leaprog and conventional cascade emission, namely, two two-photon leapfrog transitions (right).

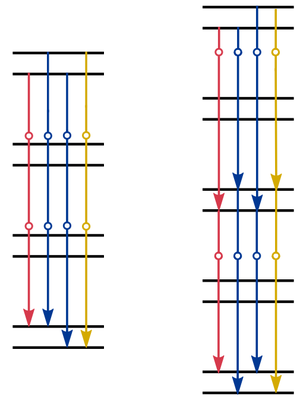
This selection has been made by Lopez Carreño et al.^[6] from a careful analysis of higher-order leapfrog transitions in the Mollow triplet, where it was found that the above processes are those observed in three-photon correlation spectra:

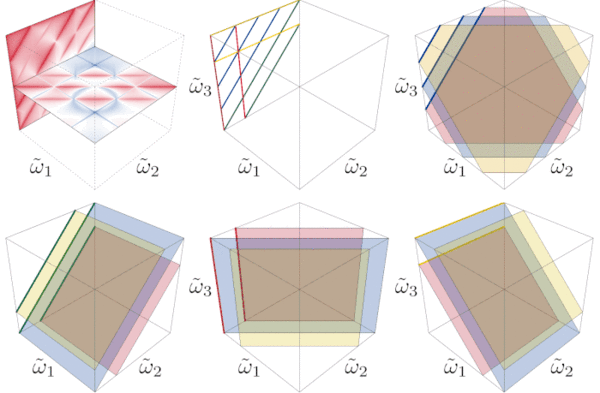
The leapfrog processes in the general case take the form of $N-1$-dimensional hyperplanes in a $N$-dimensional hypervolume. That makes normal (2D) planes in a (3D) voume for $N=3$. Still a cube is difficult to picture if it has a complex structure, so we show cuts instead. The three-photon spectrum consists of lines, each of which can be shown to belong to intersections of leapfrog planes. Although photon correlations therefore become rapidly very complex, they are, at a conceptual level, fairly simple and succinctly described by the leapfrog picture. Such high-photon number physics is a nascent field and here as well it is being led by the Muller's group, who made impressive pioneering three-photon correlation measuremnts^[7]:

The knowledge of such rich multi-photon correlations call for numerous applications. We have ourselves proposed a new type of quantum source, the bundler, that consists basically in opening a channel of emission for the leapfrog transitions, so that instead of waiting that they happen by chance in spontaneous emission, we Purcell-enhance them with a cavity. Surprisingly, we found that one can in this way bring all the emission of the system to be emitted through the leapfrog processes^[8]. This means that one can in this way emit light in groups of $N$-photons for integer $N$, or photon-bundles.

Links

Two-photon spectra of quantum emitters, open access paper with a great introductory video.
The Solid State quantum optics LAB of Andreas Muller, who first observed experimentally the leapfrog processes.

Contents

Leapfrog

Links

References

Further reading