Wading through the Hilbert space

⇠ Back to Blog:Science

The Hilbert space is a big place. In the words of Douglas Adams (?!):

Bigger than the biggest thing ever and then some. Much bigger than that in fact, really amazingly immense, a totally stunning size, real 'wow, that's big', time. Infinity is just so big that by comparison, bigness itself looks really titchy. Gigantic multiplied by colossal multiplied by staggeringly huge is the sort of concept we're trying to get across here.

We think we know it well because its canonical basis makes it look easy. Every member of the space comes in the form:

$$\sum_{k=0}^{\infty} \alpha_k\ket{k}$$

Really easy. The $\alpha_k$ are complex and they have to be normalized, $\sum_{k=0}^\infty|\alpha_k|^2=1$, but this is just basic linear algebra stuff.

That is actually deceiving as we're not quite gifted in imagining all the structure that may arise from an infinite set of complex numbers. When we think of quantum states, we think in terms of families. The simplest ones are those that constitute the canonical basis, the Fock states $\ket{k}$. That's one photon for you: $\ket{1}$.

Then, since Glauber, we know of coherent states $\ket{\alpha}$, Poissonian superpositions of photons, and thermal (also called "chaotic") states, with exponentially decaying probabilities from the vacuum. Thermal states are also statistical mixtures but that doesn't matter too much. Oh, and I forgot vacuum $\ket{0}$ although we mentioned it already. That's already quite of a good collection. I'm sure I wasn't the first but in 2006 I introduced mixtures of thermal and coherent, that I called, rather loosely, "cothermal states". You can also interpolate between Fock and coherent states. I don't know of interpolations between Fock and thermal states but this is certainly not difficult to work out. There is also the big family of squeezed and Gaussian states.

Still, all these states are far from providing even a small portion of what populates the whole Hilbert space, even though they are the most important instances.

Why would you care? Besides curiosity, a first reason came from our exciting with quantum light line of research. When you excite something with any of the funny new sources that we develop, you typically bring your target in a quantum state that is not a member of the family above (showing again how it fails to be comprehensive; our first exploration already brought us away from the lobby of the Hilbert hotel).

Take the simplest source, the single photon source (SPS). How does a quantum harmonic oscillator swing when you drive it with a SPS? It's not a Fock state $\ket{1}$. What is it? (it's easy, compute it). But more than that, what could it be? What states can we drive with a SPS? What states can we drive with any source at all? What states are in fact possible?

With Eduardo Zubizarreta Casalengua, a Master student (who got most of these results even before starting his master), we worked out in detail a new charting of the Hilbert space, that we had introduced earlier. The rulers are the Glauber correlators, $n_0$ (the mean population) and $g^{(n)}$, the $n$th order coherence function:

$$g^{(n)}\equiv\langle a^{\dagger n}a^n\rangle/\langle\ud{a}a\rangle^n\,,$$

where $a$ is the annihilation (ladder) operator.

This is how the Hilbert space for up to 3 particles (we call it $\mathcal{H}_3$) looks like:

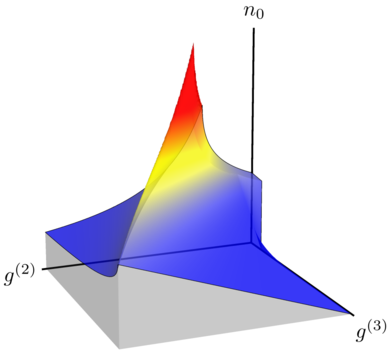
(we address $\mathcal{H}_2$ and some generic features of $\mathcal{H}_N$ in the text.) Since we have three particles at most, $g^{(4)}$ and all higher $g^{(n)}$ are here zero, so we can move in a 3D space. What this shows is the boundary for the allowed physical states (that exist for a given $(n_0, g^{(2)}, g^{(3)})$. Everything above this circumvoluted surface is forbidden, everything below till the bottom plane (set by $n_0=0$) is allowed. This is an infinite volume as although $n_0\le 3$, both $g^{(2)}$ and $g^{(3)}$ can take arbitrary values. In addition to the sole boundary, we have also worked out the density of states $\mathcal{P}_g \left( n_0, g^{(2)},g^{(3)}\right)$ populating the Hilbert space charted in this way, which is indicated on the surface only through the colour (which could also be extended to the space below, which we don't do here for clarity). The expression for the density of probability is remarkably simple (you can find it in the text, Eq. (25)) and depends only on the population... but it is defined in a complex geometrical space. Considering projections allows to get a better grip of how the states are distributed:

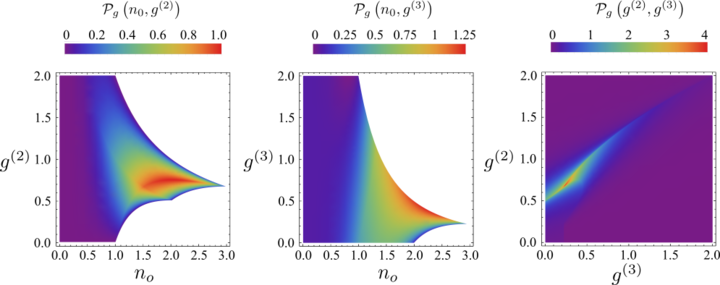
If you pick up a state randomly that has at most 3 particles, i.e., of the type $\alpha_0\ket{0}+\alpha_1\ket{1}+\alpha_2\ket{2}+\alpha_3\ket{3}$, these are the chances that you will find it with such and such a population and particle fluctuations. Importantly, there are some limits to the allowed values you will get. Namely, your state has to satisfy:

$$\max\left( n_0 g^{(3)},\frac{n_0 g^{(3)}}{3}+\frac{2}{n_0}-\frac{2}{n_0^2}\right) \leq g^{(2)}\leq\frac{n_0g^{(3)}}{2} + \frac{1}{n_0}\,,$$

and

$$\frac{2 g^{(2)}}{n_0}-\frac{2}{n_0^2}\leq g^{(3)}\leq\min\left(\frac{g^{(2)}}{n_0},\frac{3 g^{(2)}}{n_0}-\frac{6}{n_0^2}+\frac{6}{n_0^3} \right)\,,$$

as well as a condition on $n_0$ which is however too big to be written there (cf. Eqs. (28,29,35—36) of the text). As you see, your particle fluctuations are bounded both from above and below. So it's not like you can go anywhere. Granted, this is for a truncated space, and the lack of enough particles could understandably cramp the span of your reach. Note however particular that even if you allow a maximum of 3 particles, you can get arbitrarily high superbunching, by allowing $n_0$ to be small (note the $1/n_0$ divergence on the rhs).

Anyway, it is true that adding more particles wins more space. But not all the space. These are the boundaries for arbitrary $N$ (the case $N=3$ gives the conditions for the lhs and rhs of the above inequalities to be valid as well, as not all combinations of $n_0$ and $g^{(2)}$ or $g^{(3)}$ are allowed):

$$ \frac{\lfloor n_0 \rfloor !}{(\lfloor n_0 \rfloor-k)!n_0^k} \left(1+ \frac{k(n_0-\lfloor n_0 \rfloor)}{\lfloor n_0 \rfloor+ 1 - k} \right) \leq g^{(k)} \leq \frac{(N-1)!}{(N-k)!} \frac{1}{n_0^{k-1}}$$

From this expression, one sees that with increasing $N$, the rhs becomes unbounded, i.e., with enough particles, you can get $g^{(k)}$ as large as you want for any population $n_0$ and order $k$ of the correlation. However, the lhs does not depend on $N$, and while $n_0$ can now take larger values (up to $N$), it cannot access smaller values of $g^{(k)}$. This is how increasing portion of the $(n_0,g^{(2)})$ space get covered with increasing $N$ (a similar result holds for $(n_0,g^{(k)})$):

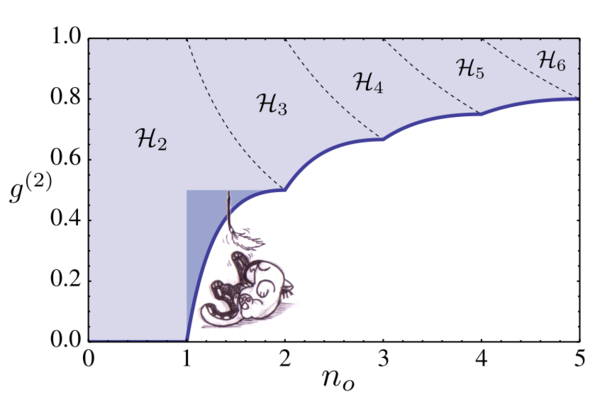
The white area (where Schrödinger's cat is playing) is forbidden, there are no states in the Hilbert space providing such combinations of populations and intensity fluctuations.

As an illustration that this relief of the Hilbert space is not familiar even to those who are used to cruise its waters, we have highlighted the area of possible states such that $g^{(2)}<1/2$ and $n_0>1$. That is, states with more than one particle on average, but an antibunching smaller than 0.5. The point is that $g^{(2)}<0.5$ has been "accepted" as a criterion for single-photon sources or single-photon states, the logic being that since $\ket{2}$ has a $g^{(2)}$ of 0.5, anything with a smaller $g^{(2)}$ has to have one particle at most. This is badly broken logic (since the $g^{(2)}$ should not then be merely smaller than 0.5, but exactly 0). Going deeper into this question is the topic of another work, our Criterion for single-photon source, and I will postpone further discussion about this too when the paper will be published, although you can already consult the work itself, arXiv:1610.06126. Instead, as a conclusion, I will list below a collection of how this oversight of the structure of the Hilbert space has been repeated throughout the years and throughout journals, including from some of the most distinguished scientists of the field writing in the most distinguished places:

This is from Michler  et al.: (here they don't refer explicitly to the 1/2)

but they do in this text:A Quantum Dot Single-Photon Turnstile Device. P. Michler, A. Kiraz, C. Becher, W. V. Schoenfeld, P. M. Petroff, Lidong Zhang, E. Hu and A. İmamoğlu in Science 290:2282 (2000).

This is from Becher  et al.:

This is from Dong  et al.:

This is from Verma  et al.:

This is from Buckley  et al.

the presence of a single quantum emitter can be confirmed by measuring $g^{(2)}(0) < 1/2$.

As shown by Grunwald,, $g^{(2)}<1/2$ proves that the state has a $\ket{1}$ component. It is probably not what the Authors meant above although literally it can be interpreted as such.

This is from Di Martino  et al. (supplementary material):

This is from Matthiesen  et al. (supplementary material, they also have the 1/2 lines in the main text but do not comment on their meaning):

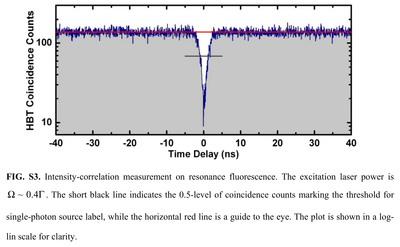
This is from Lukishova  et al.:

This is from Nothaft et al.:

They also refer to $g^{(2)}(\tau)$, not $0$ and sub-Poissonian is less than~1, not 1/2.

This is from Reimer  et al.:

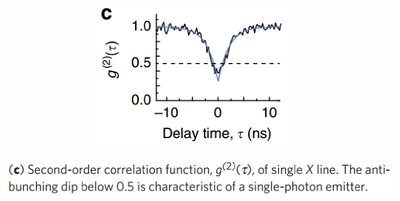
This is from Lukishova  et al.:

This is from Leifgen  et al.:

This is from Tran  et al.:

</wz ></center>

This is from Palacios-Berraquero  et al.:

This is from Schwendimann et al..:

The statement made here (when $g^{(2)}(0)<0.5$ it is highly probable that one photon states are produced) is not technically wrong. References 20, 21 are, respectively:

• Photon antibunching from few quantum dots in a cavity. C. Gies, F. Jahnke and W. W. Chow in Phys. Rev. A 91:061804(R) (2015).
• Coherent generation of nonclassical light on chip via detuned photon blockade. K. Müller, A. Rundquist, K. A. Fischer, T. Sarmiento, K. G. Lagoudakis, Y. A. Kelaita, C. Sánchez Muñoz, E. del Valle, F. P. Laussy and J. Vučković in Phys. Rev. Lett. 114:233601 (2015).

Gies  et al. make an interesting point on the disconnection of $g^{(2)}$ with the assumed quantum state (though not getting into details).

This is from Kaupp  et al., who get their own 1/2 criterion (it is not explained how background fluorescence relaxes the condition to 0.7):

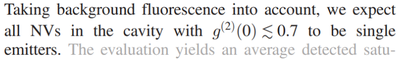
Taking background into account relaxes it to $g^{(2)}\lesssim0.7$.

This is from Bogdanov  et al., who make a selection whereby "Only emitters with antibunching characterized by $g^{(2)}<0.5$ were selected to be part of the statistics", which is fair enough. However, the following statement is later found which suggests that the criterion $1/2<g^{(2)}<2/3$ is used for two-photon emission:

$g^{(2)}>0.5$ 'points towards' two emitters!

The same authors (plus Kildishev), in Ref. , further strengthen this impression by making a similar statement for $g^{(2)}<0.5$:

This is from Arakawa  et al.:

This is from Hsiao  et al.:

This is from Boll  et al.:

This is from Fiedler et al.:

Although in this case, they have some rationale for the attribution (cf. their Eq. (1) as well as Ref. ).

This is from Stachurski et al.:

You also hear it quite a lot in conferences, which is more difficult to reproduce, although you see it in posters too, e.g., this is from Heindel  et al. [1]:

This result, that $g^{(2)}<1/2$ is no guarantee to have less than one particle, even on average (which is a stronger condition than allowing a nonzero probability for n>1 particles) has been publicly announced for the first time in March 2016, at the occasion of the Solid State Quantum Photonics in Sheffield. It is now published. We will keep a list of papers we flag that still use this criterion, apparently sexy enough to have seduced a crowd of experts who got lost at the first corner of the Hilbert space.

References

— Fabrice • 19:12, 29 May 2017