Hydrogen wavefunctions
Now that we have the closed-form analytical expressions for the Hydrogen wavefunctions, namely:
$${\displaystyle \psi _{n\ell m}(r,\theta ,\varphi )={\sqrt {{\left({\frac {2}{na_{0}^{*}}}\right)}^{3}{\frac {(n-\ell -1)!}{2n(n+\ell )!}}}}e^{-\rho /2}\rho ^{\ell }L_{n-\ell -1}^{2\ell +1}(\rho )Y_{\ell }^{m}(\theta ,\varphi )}$$
(where $\rho=2r/(na_\mathrm{B})$, $L$ are Laguerre polynomials $Y$ spherical harmonics) we can turn to the problem of their visualisation. At a technical level, this seems a fairly simple problem, since we merely have a 3D, in principle complex-valued but in many instances actually real-valued, function, which we can represent using a variety of techniques from computer graphics. We shall see that, however, one thing is to make a pretty picture, the other is to have an informative, clear, accurate and quantitatively correct picture. The latter case proves to be much more challenging and requires a combination of various representations.
At a deeper level, this also brings us into the problem of what it is we are actually looking at. At the level of the formalism, there is no ambiguity: we are looking at the density of probability amplitude of the electron distribution in space. Probability amplitude means that its modulus square gives the probability. Even with this correct and full understanding, this tells us little about what the electron itself actually is. It tells us, to be sure, where it can be found upon measurement, not quite what it actually is. Is it a diffuse wave like the wavefunction? Is it on the opposite a tiny particle that obeys to (or agrees with) the mathematics of the wavefunction? It is tempting to associate the mathematical apparatus to the physical object it describes. We shall see this quickly reaches its limits when turning to multiple particles. To this day, nobody knows what exactly is an electron and how it does bind to its nucleus. Still, for convenience, one typically regards the wavefunction as a sort of electronic cloud. In this process, we call them "orbitals" instead. So we come back to the mere "technical" problem of visualizing the well-defined wavefunction as a mathematical object. Given the structure of the solution $\psi_{nlm}=R_nY_l\m$, it is, in essence, a combination of a radial part (a combination of $r^l\exp(-r)$ [the peeled-off] with Laguerre polynomials) with a more structure angular part. The former part constitutes the full problem for $l=0$ as there is rotational symmetry.
The latter part consists exactly of the well-known spherical harmonics, which play a role when $l\neq 0$, at which step the problem becomes non-radially symmetric and raises one step up in complexity. The visualization of spherical harmonics alone can be done in 3D using the radial distance to give the magnitude of the function for each $(\theta, \phi)$ angles, which is possible to do since spherical harmonics are defined on the sphere and do not depend on $r$. The colour gives the sign, and we find these characteristic structures:
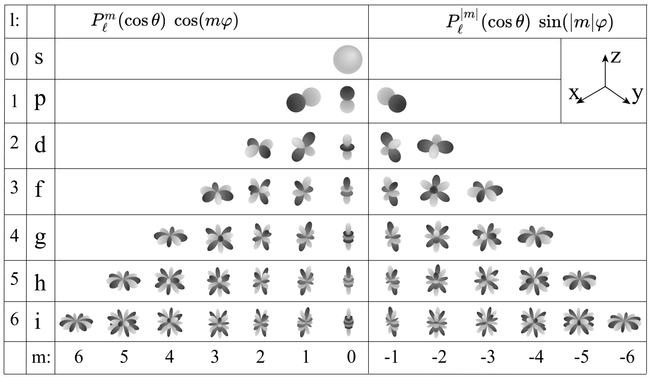
Of course when plotting in 3D it is possible to make it more or less pretty (see here for a 3D rendered version).
The radial parts are basically oscillating decaying exponentials, as we will see in the following. To embrace the full structure together, let us first remind the mathematical classification of the states. For hydrogen, the stationary orbitals are specified by three quantum numbers:
$$n,\quad l\quad\text{and}\quad m$$
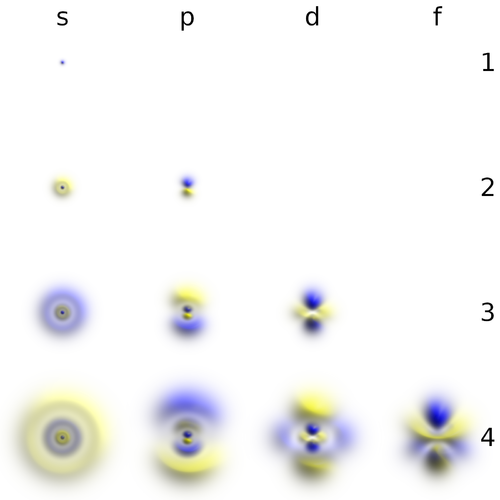
- The number $n$ or principal quantum number can take any positive integer value, $n=1, 2, \cdots$. It describes the energy and also the average distance of the electron from the nucleus, thus, qualitatively, its size. Orbitals with the same $n$ are, for this reason, collectively described as belonging to the same "shell". It already appears in the Bohr model.
- The number $l$, or azimuthal quantum number, describes the rotation, or angular momentum, of the electron. It describes, qualitatively, the shape of the orbital. It is an integer, possibly and always at least zero, otherwise strictly bounded by the principal quantum number: $0\le l\le n-1$. The orbitals with the same $n$ and $l$ are called "subshells". They are denoted $s$ (sharp) for $l=0$, $p$ (principal) for $l=1$, $d$ (diffuse) for $l=2$ and $f$ (fundamental) for $l=3$ due to historical reasons (?!) and proceed beyond that alphabetically at the exception of j which is skipped: $g, h, i, k, l, \cdots$ This gives rise to naming such as 1s ($n=1, l=0$, i.e., the ground state) or $2p$ ($n=2$, $l=1$).
- The number $m$, or magnetic quantum number, can take negative values, and is bounded in absolute value by $l$: $-l\le m\le l$. It describes, qualitatively, the orientation of the orbital.
The $s$ subshells are shaped like spheres, with the ground state being simply a fading ball. Higher $n$ with $l=0$ have radial (spherical) symmetry but with oscillations due to destructive interferences. The $s$ orbitals are the only ones with an antinode at the centre (where the nucleus is) while other orbitals present a node there. This does not invalidate the model, though, as the probability for the electron to be actually found there remain negligible.
There are three $p$-orbitals (starting at $n=2$) corresponding to $m=\pm1$ and 0. One (m=0$) has the form of two ellipsoids pointing in opposite directions and pinned by a node at the nucleus, while the two others are complex-valued and donut-shaped instead, but with the same alignment to the chosen axis (typically, $z$). This is the typical Physics' representation of the orbitals. In chemistry, linear superposition are taken so that the $m=\pm1$ wavefunctions are real-valued like the $m=0$ one, also acquiring the same bi-ellipsoidal shape but now pointing perpendicularly oriented the ones from the others, so as to be aligned with the Cartesian axis vectors $\hat\imath$, $\hat\jmath$ and $\hat k$. Such choices can also be made for the higher orbitals, in which case they share a much more uniform aspect but pointing in different directions of space. This corresponds to working with [https://en.wikipedia.org/wiki/Cubic_harmonic cubic harmonic] instead of spherical ones:
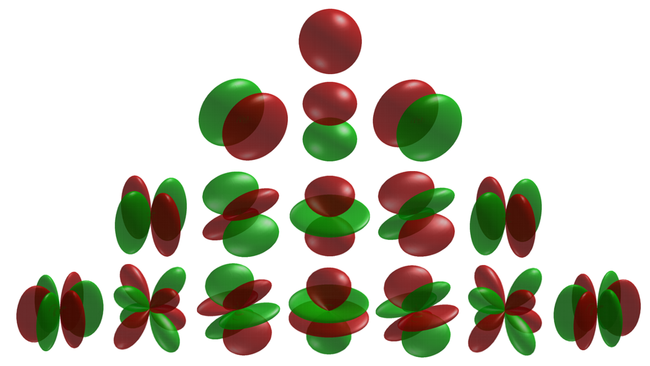
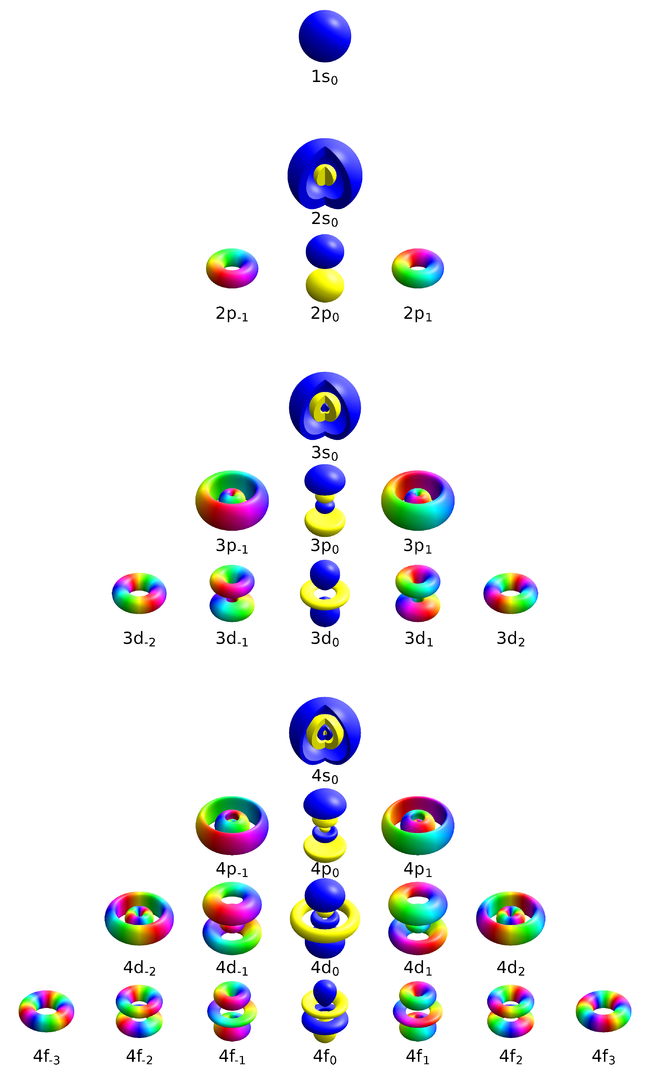
\[Alpha]0 = 1; \[Psi][n_, l_, m_, r_, \[Theta]_, \[Phi]_] := Sqrt[(2/(n \[Alpha]0))^3 (n - l - 1)!/(2 n ((n + l)!))] E^(-r/(n \[Alpha]0)) ((2 r)/(n \[Alpha]0))^l LaguerreL[n - l - 1, 2 l + 1, (2 r)/(n \[Alpha]0)] SphericalHarmonicY[l, m, \[Theta], \[Phi]]; p1 = Flatten@Table[ f = TransformedField["Spherical" -> "Cartesian", \[Psi][n, l, m, r, \[Theta], \[Phi]], {r, \[Theta], \[Phi]} -> {x, y, z}]; DensityPlot3D[Abs[f]^2 , {x, -30, 30}, {y, -30, 30}, {z, -30, 30}, ColorFunction -> Hue, ColorFunctionScaling -> True, Boxed -> False, Axes -> False, PlotLabel -> Style[StringForm["Hydrogen atom orbitals\n |\[Psi]\!\(\*SuperscriptBox[\(|\), \\(2\)]\) : n=`` l=`` m=``", n, l, m], Medium, FontFamily -> "DejaVu Serif"], LabelStyle -> {Black, Bold}, RegionFunction -> Function[{x, y, z}, x < 0 || y > 0], PlotLegends -> Automatic], {n, 1, 4}, {l, 0, n - 1}, {m, -l, l}]
- Atoms & Chemistry.
- Solid state and condensed matter.
- Variational principle.
- Perturbation theory.
- Time-dependent hamiltonians.
- Berry phase.
|}