A mechanism for a perfect single-photon source
m (Created page with "Ask someone to sketch a stream of photons in time. They will probably do something like this: --more-- This is not incorrect, especially if describing a single-photon sou...") |
m |
||
| Line 1: | Line 1: | ||
Ask someone to sketch a stream of photons in time. They will probably do something like this: | Ask someone to sketch a stream of photons in time. They will probably do something like this: | ||
| − | |||
--more-- | --more-- | ||
| Line 86: | Line 85: | ||
... | ... | ||
| − | Now we can have a look back at the literature and see if what people have reported fits somehow with our picture above. Oscillations of $g^{(2)}(\tau)$ are, of course, commonplace, simply replacing incoherent excitation by a coherent driving. Then one gets Rabi oscillations of the emitter and this syncinc ... Bunching elbows of $g^{(2)}(tau)$ are also familiar, from the snapshots a theorist can have in the back of their mind (I compiled a list in my [[Antibunching#Gallery|gallery of antibunching]]). Prospecting with that objective in mind, I believe the main experimental work in that connection is from [[Kurtsiefer]]{{etal}},{{cite|kurtsiefer00a}} with their [[Kurtsiefer00a|Stable solid-state source of single photons]].{{cite|kurtsiefer00a}} Not only do they observe this type of bunching, they also work out a nice rate-equation model based on so-called "de-shelving" (meaning, there's an intermediate state getting in the way). | + | Now we can have a look back at the literature and see if what people have reported fits somehow with our picture above. Oscillations of $g^{(2)}(\tau)$ are, of course, commonplace, simply replacing incoherent excitation by a coherent driving. Then one gets Rabi oscillations of the emitter and this syncinc ... |
| + | |||
| + | The general case is a beautiful expression: | ||
| + | |||
| + | \begin{equation} | ||
| + | \label{eq:Tue25Jul142700CEST2023} | ||
| + | g^{(2)}_N(\tau) = 1 + \sum_{p=1}^{N-1} z_N^p \exp\big(- \gamma (1- z_N^p)\tau\big) | ||
| + | \end{equation} | ||
| + | |||
| + | where~$z_N\equiv\exp\left(i{2\pi/ N}\right)$ are the $N$th roots of unity. | ||
| + | |||
| + | |||
| + | Bunching elbows of $g^{(2)}(tau)$ are also familiar, from the snapshots a theorist can have in the back of their mind (I compiled a list in my [[Antibunching#Gallery|gallery of antibunching]]). Prospecting with that objective in mind, I believe the main experimental work in that connection is from [[Kurtsiefer]]{{etal}},{{cite|kurtsiefer00a}} with their [[Kurtsiefer00a|Stable solid-state source of single photons]].{{cite|kurtsiefer00a}} Not only do they observe this type of bunching, they also work out a nice rate-equation model based on so-called "de-shelving" (meaning, there's an intermediate state getting in the way). Their theoretical analysis was undertaken earlier by [[Pegg]]{{etal}}{{cite|pegg86a}} (not known from Kurtsiefer, apparently) in much greater detail, covering various cases and different types of driving. | ||
| + | |||
| + | Interestingly, although the shape appears to be qualitatively similar, it differs in many key aspects. The reason is that, although Pegg{{etal}} refer to "cascades", they consider situations that are better seen as variations of the V and~$\Lambda$ configurations of the [[three-level system]], where the state 0 has two excited states or two ground states. In their cascades, those two states are sandwiching the zero (I refrain from writing "ground" here) state, in particular with pumping terms which kick the excitation from zero to either one or two. In contrast, our cascade is closer to what you expect from the term: something that falls down through the various levels in succession: | ||
| + | |||
| + | <center><wz tip="Our case (N=3): a 'real' cascade!">[[File:Screenshot_20240108_235250.png|175px]]</wz></center> | ||
| + | |||
| + | Our case, in the approach of Pegg{{etal}}, is described by the rate equations: | ||
| + | |||
| + | \begin{align} | ||
| + | \dot\rho_{00}&=r\rho_{11}-p\rho_{00}\,\\ | ||
| + | \dot\rho_{11}&=q\rho_{22}-r\rho_{11}\,\\ | ||
| + | \dot\rho_{22}&=p\rho_{00}-q\rho_{22}\,, | ||
| + | \end{align} | ||
| + | |||
| + | which for initial condition $\rho_{00}(0)=1$ and~$\rho_{11}(0)=\rho_{22}(0)=0$, is easily solved: | ||
| + | |||
| + | \begin{align} | ||
| + | {\rho_{00}(t)\over\rho_\mathrm{ss}}=1-e^{-(p+q+r)\frac{t}{2}} \Big\{\frac{p+q+r}{\sqrt{p^2-2 p (q+r)+(q-r)^2}}\sinh\left( \sqrt{p^2-2 p | ||
| + | (q+r)+(q-r)^2}\frac{t}{2}\right)\\ | ||
| + | +\cosh \left( \sqrt{p^2-2 p | ||
| + | (q+r)+(q-r)^2}\frac{t}{2}\right)\Big\} | ||
| + | \end{align} | ||
| + | |||
| + | The initial conditions equate this population to $g^{(2)}(t)$. Indeed, setting the parameters $p=q=r$ all equal to $\gamma$, we recover Eq. (7) of our text, i.e. (case $N=3$ of Eq. \ref{eq:Tue25Jul142700CEST2023}): | ||
| + | |||
| + | $$g^{(2)}(\tau)=1-2\sin\left({\sqrt3\over 2}\gamma\tau+{\pi\over6}\right)e^{-{3\over2}\gamma\tau}$$ | ||
| + | |||
| + | So there are several departures from Pegg{{etal}}'s seminal description: first, we extended the cascades to an arbitrary number of steps; second, we find results with a distinct physical character, namely, liquefaction of the photons in time, with oscillations and flattening of small-time correlations (opening of a gap), all this from an incoherent model. | ||
== References == | == References == | ||
<references /> | <references /> | ||
Revision as of 23:29, 8 January 2024
Ask someone to sketch a stream of photons in time. They will probably do something like this:
This is not incorrect, especially if describing a single-photon source (SPS) where photons are separated from each other. A typical such SPS, however, would more likely look like this:
Still, people would draw it as in the first case above. They would do this even in textbooks or in encyclopedias. This is for instance how Mark Fox represents antibunching in his book, Quantum Optics:

That's a bit of an idealization there. This is how the Wikipedia represents it:
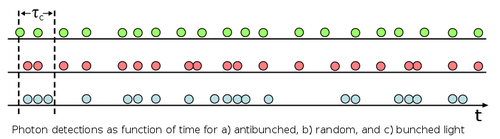
That's closer to the reality for the SPS. For the coherent stream, however, the Author—Jeff Lunden, now head of the @QuantumPhotonic group in Ottawa—had a heavy hand with so-called Poisson bursts, i.e, series of events that are very much closer to each other than you would expect when they are uncorrelated (as they happen to be for a coherent stream).
Poisson bursts are a true phenomenon, which even has its quantifier known as the burstiness. The effect was discovered by Ladislaus Bortkiewicz (Борткевич as he was Russian though he lived in Germany and was of Polish ancestry). You might also have heard of him in connection with his "economic theory of Marx", if you're into that sort of thing, but his main claim to fame is to have uncovered a fundamental effect from horse kicks in the Prussian army. His big achievement is the understanding of the law of small numbers, or the probability of very rare events but with much time for them to be realized. The book he wrote about it is where, apparently, the name of the Poisson distribution comes from.


The Poisson distribution itself indeed comes from Siméon Poisson[1] and even from before. I haven't read yet Poisson's book but it seems that he did not consider the law of small numbers, only, and on the opposite, «la loi des grands nombres» (the law of large numbers). So it was quite an insight from Bortkiewicz to uncover Poisson bursts, precisely because this involves small-probability events, for which it was difficult at the time (we're speaking about Prussia) to have the amount of big data needed to extract something significant. But Prussians were precisely the type of people who could compile in 20 volumes of Preussischen Statistik the deaths of officers from horse kicks.[2] Not something that would happen regularly but which, in the course of 20 years as was the timespan considered, can give some statistics. Bortkiewicz later used that to calibrate insurance claims and child suicide data. It remains a hotly debated phenomenon in connection with child deaths in hospitals. These happen, and when they burst, as they must if they are not correlated, of course, everybody freaks out and blames the hospital (this also happens with shark attacks, etc.)
Back to photons: in an uncorrelated stream, which Glauber tells us is what laser light is (no notion of photons in a wave, so forget about their correlations), photon-detection—if you insist in detecting your light in this way—will thus present photon bursts. This is what Jeff highlights when he shows us this ![]() . Now those happen, but are rare. The probability to have four Poisson bursts in 20 events as shown on the illusration is ... Even for the two that are unequivocal, it would already be fairly unlikely. So either they have been added by hand or the sampling repeated until something that dramatic showed up. There I can sympathize with the illustrator: it is difficult to show something compelling from Monte Carlo sampling and one has to exaggerate, or simplify, to make the point across (which is what Physics is, bringing meaning to idealized, simplified versions of reality).
. Now those happen, but are rare. The probability to have four Poisson bursts in 20 events as shown on the illusration is ... Even for the two that are unequivocal, it would already be fairly unlikely. So either they have been added by hand or the sampling repeated until something that dramatic showed up. There I can sympathize with the illustrator: it is difficult to show something compelling from Monte Carlo sampling and one has to exaggerate, or simplify, to make the point across (which is what Physics is, bringing meaning to idealized, simplified versions of reality).
Why I'm spending so much time about this is because there is a very simple way to connect the Poisson to the (conventional) antibunched stream. And this gives much insight into the behaviour or structure of the "single photons" from such a stream. By conventional SPS I mean the one you'd get by exciting from time to time a Two-Level System (SPS) and letting it emit a photon as it goes back to its ground state.
When I said that, I said everything. The antibunching emission can be seen as the sum of two Poisson processes: one to excite (randomly) the other to de-excite (also randomly). Such processes over the continuous line (time) are described by the exponential distribution. This is a central distribution in physics as it describes memoryless (i.e., uncorrelated) events. It is, for instance, the physics behind the half-life of radioactive particles (how Carbon-14 dating works, for instance).
So to make a random sampling of uncorrelated events, one can draw from the Random distribution. Say (in Julia language):
Now, whereas the sum of two (discrete) Poisson distributions is also a Poisson distribution, the sum of two (continuous) exponential distributions is something else, known as .
For simplicity of our discussion and elegance of its illustration, I will assume the rates are the same so that one can refer to the same underlying stream throughout. In this case, the distribution reduces to the so-called Erlang distribution (a special case of the more famous Gamma distribution), which was derived to compute the number of telephone calls made at the same time when people used to have an operator at a switching station.
So if you want to simulate a conventional SPS, just skip every other "photon", understanding the corresponding event as setting the 2LS in its excited state. You get something like this: (emitted photons are now sketched with a little wavy arrow).
While this is a very simple way to look at it, it's also very instructive, because, if you remember the Poisson bursts thing, then you understand that such a "mechanism" will fatally produce photons arbitrarily close in time. It will be rare indeed, but as Bortkiewicz understood with his horse kicks: give it enough time. If you wait long enough, anything can happen.
Making a "perfect single-photon source" in the sense of producing single-photons with no overlap has been a goal for many groups. Such groups want to minimize the probability that two photons be detected at exactly the same time, and so they strive to make $g^{(2)}(0)$ as small as possible.
But this is, theoretically, easy to do: the 2LS that gets excited and re-emits already does that, and indeed it's $g^{(2)}(\tau)$ is:
$$g^{(2)}(\tau)=1-\exp\big(-2\gamma\tau\big)$$
(assuming again the same rates $\gamma$ for excitaiton and de-excitation). And you can check that $g^{(2)}(0)=0$. So what's the big deal?
The big deal is that a photodetector needs some time to detect the photon. This is not an instantaneous process. Even discussed at a very fundamental level, you have to include a bandwidth~$\Gamma$ for the detector. This was highlighted by Eberly and Wòdkiewicz[3] with their introduction of what they called the "physical spectrum of light". They were worrying about time-dependent signals and, as it happens, for stationary signals, their refined treatment is not needed, one gets the same result with the famous Wiener-Khinchin theorem.
For two-photon observables (and higher-order numbers), however, Elena et al.[4] emphasized that in this case, even for stationary signals, one needs to include the detector bandwidth. If you don't do that, you look at a particular and quite unphysical limit of the problem: that of perfect time-resolution. Such a perfect time resolution is tolerable for describing a one-photon observable such as a power spectrum: there, better and better detectors will converge towards Wiener-Khinchin. But at the two-photon level, e.g., when you compute an antibunching, you lose a lot of the physics and trivialize the problem away in the perfect-detector limit. Already ten-years ago, we were drawing attention to so-called two-photon spectra at the two-photon level, and those must be defined in relation to some detector bandwidth. For them, the physical spectrum of Eberly & Wòdkiewicz becomes mandatory. When dealing with two-photons, we are one step deeper into Physics as opposed to Mathematics. In terms of antibunching, it means that one should worry not only about $g^{(2)}(0)$, which is a perfect (unphysical) detector quantity, but to $g^{(2)}(\tau)$ locally around $\tau=0$, as a real detector will be sensible with what is going there.
And what is going on for the conventional SPS is that Poisson bursts will clutter photons there.
To have a perfect SPS, one should thus open a gap. We analyzed the photon correlations in this case and, with Sana Khalid, found that it had interesting features, in particular, bunching oscillations at later times.
Our Referees (three of them) all complained in one way or the other as to the lack of some underlying mechanism to realize such a gapped source:
Being an idealized concept, such perfect single photon source is never realized in the lab. [...] While no quantum process is described or known to produce such a source, the results discussed and reported in this manuscript are still interesting from a theoretical point of view
To my opinion, the proposal of perfect single-photon sources developed in this work is rather philosophical in nature and it does not contain any concrete indications on how to build such a device or how to measure its functionality experimentally. This complicates the judgement about the validity and technical correctness of this paper.
The apparent drawback of the manuscript is that it does not present any protocol to realize the considered photon stream.
To be fair, only Referee 2 recommended against publication, thinking that the source was so as wild as to be actually unphysical and pathological, since localization of a photon in time requires complete uncertainty of its energy [...] using the known relativistic uncertainty relation ΔpΔt\sim\hbar/c, we observe that this implies also complete uncertainty of the momentum of the photon, that is complete uncertainty of the direction of the photon propagation [...] One cannot separate the photons from this source from all other photons because they can possess all energies and can propagate in any direction. The latter is even more restrictive than the former for the usual optical table setups. Put like this, it could indeed frighten an editor, but while consequences of photons-at-all-energies having a bearing on the matter (the comments of this Referee not being as silly as they look) they do not make the source unphysical.
In fact, it is possible to provide a mechanism to approach such a scenario of opening a gap in time, making the photons increasingly repulsive, as much as we want, with the result of their long-time correlations exhibiting the peaks of liquefaction. This simple, basic fundamental, we provide with Eduardo in our last paper. It consists in
The idea is as simple as considering not two steps (excitation, de-excitation) but $N$ steps: you excite, and, say, fall down a cascade, until eventual emission. Still keeping all the rates the same, we get something like this:
...
And if we keep increasing the number of steps and look at long times, see what happens:
...
Now we can have a look back at the literature and see if what people have reported fits somehow with our picture above. Oscillations of $g^{(2)}(\tau)$ are, of course, commonplace, simply replacing incoherent excitation by a coherent driving. Then one gets Rabi oscillations of the emitter and this syncinc ...
The general case is a beautiful expression:
\begin{equation} \tag{1} g^{(2)}_N(\tau) = 1 + \sum_{p=1}^{N-1} z_N^p \exp\big(- \gamma (1- z_N^p)\tau\big) \end{equation}
where~$z_N\equiv\exp\left(i{2\pi/ N}\right)$ are the $N$th roots of unity.
Bunching elbows of $g^{(2)}(tau)$ are also familiar, from the snapshots a theorist can have in the back of their mind (I compiled a list in my gallery of antibunching). Prospecting with that objective in mind, I believe the main experimental work in that connection is from Kurtsiefer et al.,[5] with their Stable solid-state source of single photons.[5] Not only do they observe this type of bunching, they also work out a nice rate-equation model based on so-called "de-shelving" (meaning, there's an intermediate state getting in the way). Their theoretical analysis was undertaken earlier by Pegg et al.[6] (not known from Kurtsiefer, apparently) in much greater detail, covering various cases and different types of driving.
Interestingly, although the shape appears to be qualitatively similar, it differs in many key aspects. The reason is that, although Pegg et al. refer to "cascades", they consider situations that are better seen as variations of the V and~$\Lambda$ configurations of the three-level system, where the state 0 has two excited states or two ground states. In their cascades, those two states are sandwiching the zero (I refrain from writing "ground" here) state, in particular with pumping terms which kick the excitation from zero to either one or two. In contrast, our cascade is closer to what you expect from the term: something that falls down through the various levels in succession:
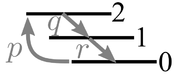
Our case, in the approach of Pegg et al., is described by the rate equations:
\begin{align} \dot\rho_{00}&=r\rho_{11}-p\rho_{00}\,\\ \dot\rho_{11}&=q\rho_{22}-r\rho_{11}\,\\ \dot\rho_{22}&=p\rho_{00}-q\rho_{22}\,, \end{align}
which for initial condition $\rho_{00}(0)=1$ and~$\rho_{11}(0)=\rho_{22}(0)=0$, is easily solved:
\begin{align} {\rho_{00}(t)\over\rho_\mathrm{ss}}=1-e^{-(p+q+r)\frac{t}{2}} \Big\{\frac{p+q+r}{\sqrt{p^2-2 p (q+r)+(q-r)^2}}\sinh\left( \sqrt{p^2-2 p (q+r)+(q-r)^2}\frac{t}{2}\right)\\ +\cosh \left( \sqrt{p^2-2 p (q+r)+(q-r)^2}\frac{t}{2}\right)\Big\} \end{align}
The initial conditions equate this population to $g^{(2)}(t)$. Indeed, setting the parameters $p=q=r$ all equal to $\gamma$, we recover Eq. (7) of our text, i.e. (case $N=3$ of Eq. (1)):
$$g^{(2)}(\tau)=1-2\sin\left({\sqrt3\over 2}\gamma\tau+{\pi\over6}\right)e^{-{3\over2}\gamma\tau}$$
So there are several departures from Pegg et al.'s seminal description: first, we extended the cascades to an arbitrary number of steps; second, we find results with a distinct physical character, namely, liquefaction of the photons in time, with oscillations and flattening of small-time correlations (opening of a gap), all this from an incoherent model.
References
- ↑ Probabilité des jugements en matière criminelle et en matière civile, précédées des règles générales du calcul des probabilités, S. Poisson, Paris, France: Bachelier (1837).
- ↑ Bortkiewicz's Data and the Law of Small Numbers. M. P. Quine and E. Seneta in Stat. Rev. 55:173 (1987).
- ↑ The time-dependent physical spectrum of light. J.H. Eberly and K. Wódkiewicz in J. Opt. Soc. Am. 67:1252 (1977).
- ↑ Theory of Frequency-Filtered and Time-Resolved $N$-Photon Correlations. E. del Valle, A. González-Tudela, F. P. Laussy, C. Tejedor and M. J. Hartmann in Phys. Rev. Lett. 109:183601 (2012).
- ↑ 5.0 5.1 Stable Solid-State Source of Single Photons. C. Kurtsiefer, S. Mayer, P. Zarda and H. Weinfurter in Phys. Rev. Lett. 85:290 (2000).
- ↑ Correlations in light emitted by three-level atoms. D. T. Pegg, R. Loudon and P. L. Knight in Phys. Rev. A 33:4085 (1986).