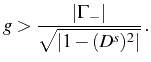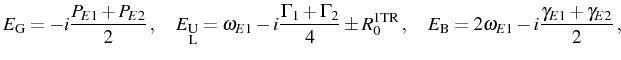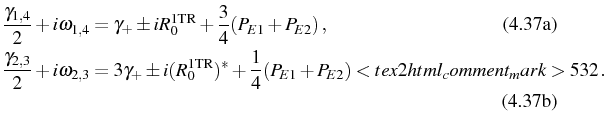The effect of the pump and the SC/WC phase space

The different regions that can appear when the incoherent continuous pump is turned on, are plotted in Fig. 4.4 as a function of the pumping rates. All the possibilities are defined in terms of $\Re{(z_1)}$ and $\Re{(z_2)}$ being zero or not. The conditions arising are linked to (that can only be real or pure imaginary) although not so straightforwardly as in the absence of pump.

**Figure 4.4:** Phase space of the SS strong/weak coupling regimes as a function of pump for $\gamma_{E1}=g$ and $\gamma_{E2}=g/2$ . In strong coupling (SC, blue), one can distinguish two regions, the more extended first order (FSC, light blue) and the second order (SSC, dark blue) strong coupling. The weak coupling regime (WC) is shaded in purple and the mixed coupling regime (MC), with two transitions in SC and two in WC, in green. The dashed blue lines enclose the two regions where two peaks can be resolved in the direct emission of the first QD, $S_1(\omega)$ . One falls in SC and the other in WC. Six points are marked with letters (a)-(f) for a latter analysis. The red solid line delimits the region (from above) where the SS is reached in the LM, always in SC for these decay parameters.
$\includegraphics[width=0.7\linewidth]{chap4/Fig3.ps}$

The most extended region is the standard (First order) Strong Coupling (FSC, in light blue), which includes the SC regime in the absence of pump. The situation with the levels is that of Fig. 4.1(b). It is characterized by

$\displaystyle R=\vert R\vert\in \mathbb{R}\quad\Leftrightarrow \quad G^2>g^2-\Gamma_-^2\,,$

(4.31)

from what follows that

, and therefore $\Re{(z_1)}=\Re{(z_1)}\neq 0$ . Note that this requires

$\displaystyle g>\frac{\vert\Gamma_-\vert}{\sqrt{\vert 1-(D^s)^2\vert}}\,.$

(4.32)

The two pairs of peaks 1, 4 and 2, 3 are placed one on top of each other although they are differently broadened [see the spectra of Fig. 4.3 and of Fig. 4.5(a) and (d)]. In this region,

, so it is not possible to reach the optimum effective coupling and maximum splitting of the lines given by $\sqrt{2}g$ .

In Fig. 4.6(a) and (b) we track the broadenings and positions of the four peaks (1 and 4 in blue and 2 and 3 in red) as a function of pump, through the SC region of Fig 4.4, on the line $P_{E2}=P_{E1}/2$ . Following them from zero pump, where the manifold picture is exact, the four peaks can be easily associated with the lower and upper transitions of Fig. 4.1(b), and that is why we use the same color code. The dressed states $\ket{U}$ and $\ket{L}$ exist but with energies $\omega_{E1}\pm\Re{(z_1)}$ , both affected equally by decoherence.

**Figure 4.5:** A set of spectra for $\gamma_{E1}=g$ and $\gamma_{E2}=g/2$ sampling all the different regions of Fig 4.4. The pump parameters of each plot are marked with their corresponding letter (a)-(f) in the phase space plot 4.4. The final spectral line (in thick solid black) is decomposed into two pairs of symmetric peaks (thin red-blue or green-orange) in SC and four peaks centered at zero in WC. The positions of these peaks are marked with vertical lines of the corresponding colors. The LM spectra (purple dashed), always in SC, is composed of only two peaks marked also with vertical lines for comparison.
$\includegraphics[width=0.45\linewidth]{chap4/Fig2a.eps}$ $\includegraphics[width=0.45\linewidth]{chap4/Fig2b.eps}$ $\includegraphics[width=0.45\linewidth]{chap4/Fig2c.eps}$ $\includegraphics[width=0.45\linewidth]{chap4/Fig2d.eps}$ $\includegraphics[width=0.45\linewidth]{chap4/Fig2e.eps}$ $\includegraphics[width=0.45\linewidth]{chap4/Fig2f.eps}$

By construction, the resulting spectra in this regime can only be a doublet [Fig. 4.5(a)] or a single peak [Fig. 4.5(d)], depending on the magnitude of the broadening of the peaks (that always increases with pump and decay) against the splitting of the lines (that always decreases). As in the LM, observing a doublet in the spectra is not granted in SC, but here the tendency is always the same: the lower the pump and the decay, the better the resolution of the splitting.

The second situation, the Rabi frequency being imaginary,

$\displaystyle R=i\vert R\vert\quad\Leftrightarrow \quad G^2>g^2-\Gamma_-^2\,,$

(4.33)

opens three possibilities, that constitute the three remaining regions in Fig. 4.4. In what follows we assume condition Eq. (4.33) and add new conditions to define the three such regions.

The Weak Coupling regime (WC, in purple) is characterized by

$\displaystyle z_1=i\vert z_1\vert\neq z_2=i\vert z_2\vert\quad\Leftrightarrow \quad G<\vert\Gamma_+-\vert R\vert\vert$

(4.34)

and therefore $\Re{(z_1)}=\Re{(z_1)}=0$ . Note that condition (4.34) is not analytical in terms of the relevant parameters (4.25). The four peaks are placed at the origin with four different broadenings. The dressed states $\ket{U}$ and $\ket{L}$ have collapsed in energy to $\omega_{E1}$ . Again, this does not mean that the resulting spectra is always one peak [as in Fig. 4.5(e)], it can be a doublet when a thin negative Lorentzian carves a hole in a positive Lorentzian, due to the interference between the modes [as in Fig. 4.5(f)].

Up to here, we have studied the SC and WC as they appeared defined in the LM. We find a new region of SC, when both parameters $z_{1,2}$ are real and

$\displaystyle z_1=\vert z_1\vert< z_2=\vert z_2\vert\quad\Leftrightarrow \quad G>\vert\Gamma_++\vert R\vert\vert\,.$

(4.35)

We call it Second order Strong Coupling regime (SSC, colored in dark blue in the phase space). Here, the broadenings of the four peaks are equal, $\gamma_p/2=2\Gamma_+$ , but the positions of the pairs of peaks are different, $\omega_{1,4}=\pm \vert z_1\vert$ and $\omega_{2,3}=\pm \vert z_2\vert$ . The reason is that the bare energies of the modes undergo a second order anticrossing induced by the interplay between coupling, pump and decay. The energies of the dressed states are affected differently by decoherence, up to the point where we should consider new eigenstates. In Fig. 4.1(c), we have plotted these states, $\ket{I}$ and $\ket{O}$ , that have energies not splitted symmetrically around $\omega_{E1}$ , but rather at $+\vert z_1\vert$ (giving rise to the inner peaks, in green) and $-\vert z_2\vert$ (giving rise to the outer peaks, in orange).

We can see how peak broadenings and positions change when going from FSC to SSC in Fig. 4.6(c)-(d). In this case, we track the peaks by varying $P_{E2}$ for fixed $P_{E1}$ , moving from the points (a) to (c) in the phase space. The first vertical line marks the border between the two kinds of SC, with the opening of a ``bubble'' for the positions $\omega_1$ and $\omega_2$ (that were equal in the FSC region), and the convergence of all the broadenings. The spectrum we choose from this region, Fig. 4.5(b), features a single peak despite the subtle underlying structure. In principle, quadruplets and triplets can form out of the four peaks. However, the broadenings and contributions of the dispersive parts () are too large to let the fine splittings emerge clearly. The spectra in this region are singlets and doublets but we will see in Sec. 4.4 with other examples, that they can be very distorted, undoubtly reflecting the multi peaked structure.

The last new region in Fig. 4.4, appears when is imaginary and real, or equivalently,

$\displaystyle z_1=i\vert z_1\vert\,,\quad z_2=\vert z_2\vert\quad\Leftrightarrow \quad \vert\Gamma_+-\vert R\vert\vert<G<\vert\Gamma_++\vert R\vert\vert\,.$

(4.36)

This is a Mixed Coupling regime (MC, colored in green in the phase space) where the two inner peaks, 1 and 4, have collapsed at the origin in WC, and so has the associated eigenstate $\ket{I}$ . The two outer peaks, 2 and 3, are still splitted and so is $\ket{O}$ . The spectrum in Fig. 4.5(c) is an example of this region, too broadened to reveal its structure. Again, although a triplet seems possible, distorted singlets are the only outcome in the best of cases due to the broadening and dispersive parts. In Fig. 4.6(c)-(d) we can see the transition from SSC into MC, at the second vertical line.

**Figure 4.6:** Broadenings (a), (c), and positions (b), (d) of the lines that compose the spectra as a function of pump for the decay parameters $\gamma_{E1}=g$ and $\gamma_{E2}=g/2$ . In the plots of the first column, the pump $P_{E1}$ varies with $P_{E2}=P_{E1}/2$ , moving in the phase space of Fig 4.4 from point (a) to (d). The vertical line shows the crossing from FSC to WC. In the plots of the second column, the pump $P_{E2}$ varies with $P_{E1}=0.2g$ , moving in the phase space of Fig 4.4 from point (a) to (c). The vertical lines show the crossing from FSC to SSC and finally to MC. In all the plots, the thick solid lines are the exact results [Eqs. (4.19)] while the thin ones are the approximated results from the manifold method [that follow from Eqs. (4.37)]. The dashed blue line represents the splitting as it is resolved in the final spectrum (4.11). The code of colors (red-blue and orange-green) corresponds to that of the transitions in Fig. 4.1 and the associated peaks in Fig. 4.5.
$\includegraphics[width=\linewidth]{chap4/Fig4.ps}$

The manifold picture successfully associates the peaks that compose the spectrum of emission to transitions between the levels. In order to understand better some features of the spectra of the SS under incoherent pump in the different regions that we have defined, we will now push the manifold method--adequate for vanishing pump--a bit further. Note that, in this system, the pumping mechanism is of the same nature than the decay, due to the saturation of both QDs and the symmetry in the schema of levels that they form. The master equation is symmetrical under exchange of the pump and the decay ( $\gamma_{Ei}\leftrightarrow P_{Ei}$ ) when the two levels of both 2LS are inverted ( $G\leftrightarrow B$ and $E1\leftrightarrow E2$ ).^4.2 Consequently, the parameters , and , and also the populations of all the levels, are symmetric in the same way, as it happens with just one 2LS (see Sec. 2.5.1). In other systems we study in this manuscript, like the LM, the JCM or simply the single HO, the effect of the pump extends upwards to an infinite number of manifolds while the decay cannot bring the system lower than the ground state. There is no natural truncation for the pump (that ultimately leads to a divergence), as there is for the decay. But with coupled 2LSs, state $\ket{B}$ is the top counterpart of $\ket{G}$ , undergoing a saturation when pump or decay is large, respectively. This implies, for instance, that the spectra in the limit of vanishing decay is exactly the same as that of vanishing pump and that in such case we can also apply the manifold method to obtain the right positions and broadenings as a function of pump, in the same way that we did as a function of decay only. We only have to take into account the mentioned symmetry consistently. As long as the dynamics moves upwards or downwards only, even when intermediate states are coupled, the manifold method is suitable.

The manifold diagonalization breaks, however, in the presence of both nonnegligible pump and decay. If we combine their effects in the nonhermitian Hamiltonian as

$\displaystyle E_\mathrm{G}=-i\frac{P_{E1}+P_{E2}}{2}\,,\quad E_{\substack{\math... ...rm{1TR}\,,\quad E_\mathrm{B}=2\omega_{E1}-i\frac{\gamma_{E1}+\gamma_{E2}}{2}\,,$

(4.37)

we do not obtain the right results of four--in principle different--peaks but rather the standard pairing with

$\begin{subequations}\begin{align}&\frac{\gamma_{1,4}}{2}+i\omega_{1,4}=\gamma_+\... ...}{4}(P_{E1}+P_{E2}) <tex2html_comment_mark>532 \,. \end{align}\end{subequations}$

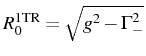These expressions bring us back to the naive association of SC with $\Re(R_0^\mathrm{1TR})\neq 0$ that we discussed Sec. 4.2.1. It is obvious that only $R_0^\mathrm{1TR}=\sqrt{g^2-\Gamma_-^2}$ , to describe the splitting between the dressed states, cannot give the variety of situations than the two parameters $z_{1,2}$ give. But there are other fundamental differences. One is the renormalization of the coupling constant into

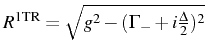, due to the interplay of pump and decay. Another one is made more clear when comparing $z_{1,2}=\sqrt{G^2-(\Gamma_-\mp iR)^2}$ (at resonance) with $R^\mathrm{1TR}=\sqrt{g^2-(\Gamma_-+i\frac{\Delta}{2})^2}$ (out of resonance). The Rabi

is acting as a complex detuning for $z_{1,2}$ , like $\Delta$ for $R^\mathrm{1TR}$ . When

is real (in FSC), it behaves like a normal real detuning, pushing all the positions outwards in the same way (see Fig. 3.3). However, if

is imaginary, it induces a difference between the real parts of

and

when they exist (SSC and MC), giving rise to a second order anticrossing.

Let us now look, for instance, at the positions and broadenings in Figs. 4.6(a) and (b). In thin lines (with the usual color code) we can see the approximate values from Eq. (4.38). Not only do they deviate quantitatively from the exact values, they are also qualitatively wrong giving too late the transition into WC and a crossing of the broadenings when they really repel and stay one above the other. The joined presence of coupling, decay and pump has a more complicated effect than simply bringing the excitations up and down the levels of Fig. 4.1. The positions and broadenings are also connected with the populations. For example, the anticrossing of the broadenings takes place at the same point where the populations of the intermediate states reach a maximum and state starts to be the most populated. By reasoning with the manifold picture, the lower transitions would have larger broadening than the upper, increasing the pump after this point. However, the emptying of levels and , seems to decelerate this intuitive tendency. Even more dramatic is the divergence between the approximate and the exact positions and broadenings in Figs. 4.6(c) and (d). Eqs. (4.38) cannot reproduce the second anticrossing, as we said.