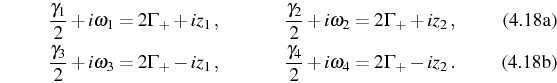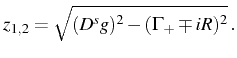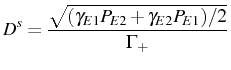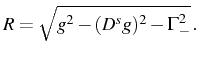Spectrum at resonance in the Steady State

The general expressions for the spectrum and correlator find a simple analytic solution at resonance, $\omega_{E1}=\omega_{E2}$ , and in the SS under incoherent continuous pump. In what follows, we refer always to such a situation and therefore drop the SS label. The four complex coefficients,

$\begin{subequations}\begin{align}l_1+ik_1=&\frac{1}{16 R z_1}\Big\{\Big[2(2z_1+i... ...a_2)-2(R+z_2-i\Gamma_+)\Big]n_\mathrm{12}\Big\}\,, \end{align}\end{subequations}$

are defined in terms of the parameters

$\displaystyle a_1=\frac{g^2}{\Gamma_+^2}[4\Gamma_+^2+2P_{E1}(P_{E2}-2\Gamma_+)-P_{E2}\Gamma_1]\,,\quad a_2=\frac{g^2}{\Gamma_+^2}P_{E1}(P_{E1}-\gamma_{E1})\,,$

(4.18)

and the corresponding frequencies and decay rates

$\begin{subequations}\begin{align}&\frac{\gamma_1}{2}+i\omega_1=2\Gamma_++iz_1\,,... ...ad &\frac{\gamma_4}{2}+i\omega_4=2\Gamma_+-iz_2\,. \end{align}\end{subequations}$

They are all given in terms of two complex parameters:

$\displaystyle z_{1,2}=\sqrt{(D^sg)^2-(\Gamma_+\mp i R)^2}\,.$

(4.20)

is a real positive quantity, between 0 and $\sqrt{2}$ , given by

$\displaystyle D^s=\frac{\sqrt{(\gamma_{E1}P_{E2}+\gamma_{E2}P_{E1})/2}}{\Gamma_+}$

(4.21)

that tells about the degree of symmetry in the system. For example, it is 1 when all parameters are equal, $\gamma_{E1}=\gamma_{E2}=P_{E1}=P_{E2}$ , and 0 if one of the parameters is much larger than the others. The renormalized coupling,

$\displaystyle G=D^sg\,,$

(4.22)

reaches its maximum when the parameters are such that $D^s=\sqrt{2}$ . The enhancement by

is related to cooperative behavior of two coupled modes, similarly to the superradiance of

atoms of the Dicke model (Chapter 6) or the renormalization by

in the JCM with

photons (Chapter 5).

The last and main parameter appearing in the previous expressions is

$\displaystyle R=\sqrt{g^2-(D^s g)^2-\Gamma_-^2}\,.$

(4.23)

This is the true analog of the (half) Rabi frequency,

, in the LM [Eq. (3.33)]. We refer to it by

and not by $R_0^\mathrm{2TD}$ , as it would correspond to the two-time related quantity at resonance, for simplicity of notation. At vanishing pump, the renormalized coupling converges to

, and both

and $R_0^\mathrm{1TD}$ converge exactly to

(LM).

The normalized spectra for the direct emission of dot follows from Eq. (4.11) with the coefficients we have just obtained. It is composed of four peaks with positions and broadenings given respectively by the real and imaginary parts of and . These latter parameters are valid also in the SE case by only setting the pumping rates to zero. Fig. 4.3 is an example of the spectrum $S_1(\omega)$ we have constructed (in solid black), with its four peaks, each of them a combination of Lorentzian and dispersive parts.

**Figure 4.3:** Direct emission spectrum from QD 1 (thick solid black line) in the SC regime ( $\gamma_{E1}=g$ and $\gamma_{E2}=g/2$ ) for the SS under vanishing pump ( $P_{E1}=0.02g$ and $P_{E2}=0.01g$ ). The four peaks that compose the spectra are plotted with a thin blue line (lower transitions 1, 4) and with a thin red line (upper transitions 2, 3). The equivalent spectra in the LM is plotted with a dashed purple line for comparison. Due to the low pump, the doubly excited state $\ket{B}$ is almost empty and the emission from upper transitions very weak (magnified $\times 30$ to be visible). This is the linear regime where all models for two coupled modes converge.
$\includegraphics[width=0.7\linewidth]{chap4/Fig1.eps}$