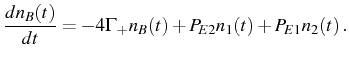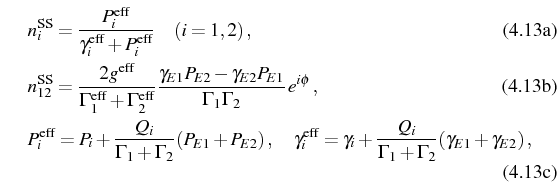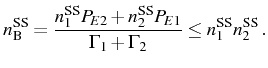Mean values
The mean values of interest can be found through the quantum
regression formula, applied on the set of correlators from the first
and second manifolds
![]() (see
Fig. 4.2) with
(see
Fig. 4.2) with
![]() and the
corresponding regression matrices. As in the LM, the correlators in
and the
corresponding regression matrices. As in the LM, the correlators in
![]() can be obtained independently solving
Eq. (3.6) with the same regression matrix
can be obtained independently solving
Eq. (3.6) with the same regression matrix
![]() and
pumping term
and
pumping term
![]() as in Eq. (3.7a),
only changing indexes
as in Eq. (3.7a),
only changing indexes
![]() and with the fermionic
parameters,
and with the fermionic
parameters,
![]() . The solutions for
. The solutions for
![]() ,
, ![]() and
and ![]() are, therefore, given by the equivalent
expressions of the LM. On the other hand,
are, therefore, given by the equivalent
expressions of the LM. On the other hand, ![]() , that belongs to
, that belongs to
![]() , finds its expression separately, only in
terms of
, finds its expression separately, only in
terms of ![]() and
and ![]() , through the equation
, through the equation
In the SE, Eqs. (3.10)-(3.11) apply for an initial state with averages
In the SS, the mean values of
![]() can be written
in terms of effective pump and decay parameters, as in the LM, but now
with the fermionic statistics:
can be written
in terms of effective pump and decay parameters, as in the LM, but now
with the fermionic statistics:
and with the corresponding Purcell rate
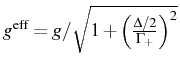 and
the phase
and
the phase
Note the difference with the equivalent
This is an interesting manifestation of the symmetry/antisymmetry of the wavefunction for two bosons/fermions, that is known to produce such an attractive/repulsive character for the correlators.4.1 Here we see that quantum (or correlated) probabilities
In the most general case, with pump and decay, from the initial to the
steady state, also the transient dynamics of the mean values are given
by the equivalent expressions from coupled bosons,
Eq. (3.88). The general ![]() must be
found by solving Eq. (4.12). We can conclude
from this, as we did for the LM, that the single-time dynamics are
ruled by the exact fermionic counterpart of the (half) Rabi frequency
in Eq. (3.12), that we will refer to as
must be
found by solving Eq. (4.12). We can conclude
from this, as we did for the LM, that the single-time dynamics are
ruled by the exact fermionic counterpart of the (half) Rabi frequency
in Eq. (3.12), that we will refer to as
![]() . In a naive approximation to the problem, following
from the abundant similarities with the LM, one could imagine that the
definitions of WC and SC regimes stem from the real part of
. In a naive approximation to the problem, following
from the abundant similarities with the LM, one could imagine that the
definitions of WC and SC regimes stem from the real part of
![]() , being zero or
not. However, we will see that this is not the case whenever pump and
decay are both taken into account. The single-time dynamics
seems to disconnect completely from the more involved SC/WC distinction
that we will find, solving the two-time dynamics.
, being zero or
not. However, we will see that this is not the case whenever pump and
decay are both taken into account. The single-time dynamics
seems to disconnect completely from the more involved SC/WC distinction
that we will find, solving the two-time dynamics.
Elena del Valle ©2009-2010-2011-2012.