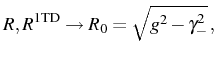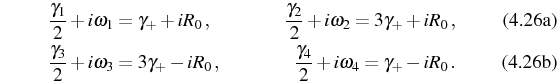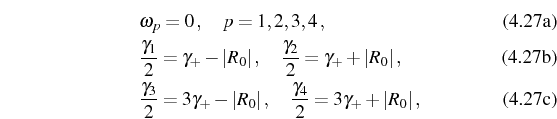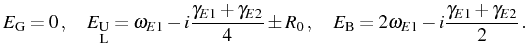Vanishing pump (and SE) case in the manifold picture
Only in the case of vanishing pump, that corresponds as well to the SE situation, the simple SC/WC classification holds. In this limit, we recover the familiar expression for the half Rabi frequency,
as in Eq. (3.33). The parameters simplify to
The two pairs of peaks
since
It it important to note that, as a result of the two pairs of peaks sitting always on the same two frequencies, the final spectra can only be either a single peak or a doublet, both shapes being possible in SC or WC regimes (as in the LM and for the same reasons).
The manifold picture (see Section 2.5.2)
gives a very intuitive derivation and interpretation of the results in
this limit. We consider the nonhermitian Hamiltonian
![]() that results from making the
substitution
that results from making the
substitution
![]() in Eq. (4.1), in order to include the decay
of the modes. Diagonalizing the Hamiltonian in the first manifold [as
with the two HOs, see Eq. (2.56) and
discussions related in Chapter 3], we obtain
in Eq. (4.1), in order to include the decay
of the modes. Diagonalizing the Hamiltonian in the first manifold [as
with the two HOs, see Eq. (2.56) and
discussions related in Chapter 3], we obtain
with dressed complex energies
Applying Eq. (2.96) between the energies in Eq. (4.30), leads to the positions and broadenings of Eq. (4.27)-(4.28) in the way that we now explain. In Fig. 4.1(a) we can see the four possible transitions in the manifold picture: one can check that
- the lower transitions (in blue), from
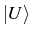 and
and 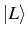 ,
coincide, respectively, with the expressions for peaks 1 and 4 in
SC, Eq. (4.27) and 1 and 2 in WC,
Eq. (4.28);
,
coincide, respectively, with the expressions for peaks 1 and 4 in
SC, Eq. (4.27) and 1 and 2 in WC,
Eq. (4.28);
- the upper transitions (in red), towards
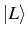 and
and 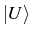 ,
coincide with the expressions for peaks 2 and 3 in SC,
Eq. (4.27) and 3 and 4 in WC,
Eq. (4.28).
,
coincide with the expressions for peaks 2 and 3 in SC,
Eq. (4.27) and 3 and 4 in WC,
Eq. (4.28).
On the other hand, the SS case in the limit of vanishing pump is
exactly the linear regime, where only the vacuum and first manifold
are populated. The spectra in this limit converge with the LM and
also it can be analyzed in terms of manifolds by extension. For
instance, the spectrum in Fig. (4.3)
corresponds to SC for vanishing pump, for
![]() and
and
![]() . The lower transition peaks, in blue, dominate over
the broader and weak upper peaks, in red, and as a result, the
splitting in dressed modes is visible in the observed spectrum, in
black. We now use this configuration in what follows to explore the
effect of the incoherent continuous pump.
. The lower transition peaks, in blue, dominate over
the broader and weak upper peaks, in red, and as a result, the
splitting in dressed modes is visible in the observed spectrum, in
black. We now use this configuration in what follows to explore the
effect of the incoherent continuous pump.
Elena del Valle ©2009-2010-2011-2012.