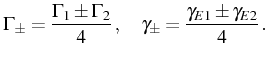Introduction

The Hamiltonian for two coupled two-level systems (2LS) reads

$\displaystyle H=\omega_{E1}\ud{\sigma_1}\sigma_1+\omega_{E2}\ud{\sigma_2}\sigma_2+g(\ud{\sigma_1}\sigma_2+\ud{\sigma_2}\sigma_1)\,,$

(4.1)

where $\sigma_{1,2}$ are the lowering operators of the 2LSs, with bare energies $\omega_{E1,E2}$ , that are coupled linearly with strength

. The Hilbert space consists of only three manifolds with zero ( $\ket{G}=\ket{g,g}$ ), one ( $\ket{E1}=\ket{e,g}$ , $\ket{E2}=\ket{g,e}$ ) and two ( $\ket{B}=\ket{e,e}$ ) excitations. The letters

and

mean the ground or exciton states in the dot. In Fig. 4.1 we can see in a schema how the intermediate levels, $\ket{E1}$ , $\ket{E2}$ , form two dressed states, $\ket{U}$ and $\ket{L}$ , with the same splitting and structure found for the harmonic oscillators (HOs) [Eqs. (2.56)-(2.57)]. This equivalence breaks in the manifold with two excitations where the statistical nature of the particles reveals and only one state is available (as compared to three in the LM, see central part of Fig. 5.5). The master equation in Eq. (2.71) can be exactly solved in this finite Hilbert space. If the pump is strong, the dots are brought to saturation in the SS, quenching the system emission and effectively decoupling the dots, but also avoiding the divergences that appeared in the LM due to bosonic accumulation. The fermionic character of both effective broadenings

$\displaystyle \Gamma_1=\gamma_{E1}+P_{E1}\,,\quad \Gamma_2=\gamma_{E2}+P_{E2}\,,$

(4.2)

results in qualitative differences that can be directly contrasted with the completely bosonic case. For later convenience, we also define the parameters:

$\displaystyle \Gamma_{\pm}=\frac{\Gamma_1\pm\Gamma_2}{4}\,,\quad \gamma_{\pm}=\frac{\gamma_ {E1}\pm\gamma_{E2}}{4}\,.$

(4.3)

**Figure 4.1:** Energy levels for the coupled QDs system described by Hamiltonian (4.1), that remain a good picture in SC. As we will see in Sec. 4.3.2, the SC regime in the absence of pump (a) separates in two regions when pump is turned on, FSC (b) and SSC (c). The dressed states $\ket{U,L}$ of SC and FSC, change in SSC into a new set $\ket{I,O}$ that are not symmetrically splitted. The thickness of the lines represents the uncertainty in energy due to (a) the decay and (b,c) both the pump and the decay. Transitions labelled 1 and 4 (in blue) are those involving $\ket{G}$ and transitions 2 and 3 (in red), those involving $\ket{B}$ . The energy and total decay rate of transitions 1 and 3 (involving $\ket{U}$ or $\ket{I}$ , in green) depend on , while 2 and 4 (involving $\ket{L}$ or $\ket{O}$ , in orange) depend on . The same color code is used in the rest of the figures for the decomposition of the spectra of emission.
$\includegraphics[width=\linewidth]{chap4/Fig0.ps}$

In this Chapter, I follow the scheme of the previous one, with the equivalent unified formalism to describe SE and SS spectra. In Section 4.2, we obtain fully analytically the luminescence spectra at resonance and the single-time dynamics thanks to the QRF. In Section 4.3 we analyze the spectra and define strong/weak coupling, first in the absence, and then including the incoherent continuous pump. In Section 4.4 we illustrate the results of previous Sections with some examples of interesting configurations. In Section 4.5 we look into the second order correlation functions. In Section 4.6, we discuss some possible future lines of investigation with this system. Finally, in Section 4.7, I give a summary of the main results and provide an index of all the important formulas and key figures of this Chapter.