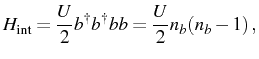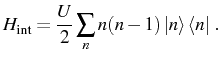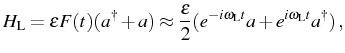Coherent coupling
Coherent processes are those that can be written as a Hamiltonian ![]() (always hermitian) and included in the Schrödinger equation:
(always hermitian) and included in the Schrödinger equation:
We already wrote the free evolution of the bosonic and fermionic fields in Eq. (2.3) and (2.47). Two fields
If the detuning between the modes,
is small as compared to the coupling, during the dynamics of
In this text, field ![]() will be always the electromagnetic field
inside a cavity, where one mode with frequency
will be always the electromagnetic field
inside a cavity, where one mode with frequency ![]() is
selected. Depending on the model for the material excitation,
is
selected. Depending on the model for the material excitation, ![]() is
described by, typically, another HO, giving rise to the linear
model (LM) developed by Hopfield (1958), or by a 2LS,
giving rise to the Jaynes & Cummings (1963) model (JCM), discussed in
the Introduction. Those are the most fundamental cases as they
describe material fields with Bose and Fermi statistics, respectively.
Possible extensions are a collection of HOs; this has been considered
by Rudin & Reinecke (1999) and more recently by
Averkiev et al. (2009), or of many 2LS like in the work of
Dicke (1954), or a three-level system as considered by
Bienert et al. (2004), etc...
is
described by, typically, another HO, giving rise to the linear
model (LM) developed by Hopfield (1958), or by a 2LS,
giving rise to the Jaynes & Cummings (1963) model (JCM), discussed in
the Introduction. Those are the most fundamental cases as they
describe material fields with Bose and Fermi statistics, respectively.
Possible extensions are a collection of HOs; this has been considered
by Rudin & Reinecke (1999) and more recently by
Averkiev et al. (2009), or of many 2LS like in the work of
Dicke (1954), or a three-level system as considered by
Bienert et al. (2004), etc...
The parameter ![]() depends on both the properties of the cavity and the
emitters:
depends on both the properties of the cavity and the
emitters:
![]() , where
, where ![]() is the effective cavity
volume and
is the effective cavity
volume and ![]() the oscillator strength of the emitter. Therefore, in
order to achieve strong coupling experimentally, the cavity must have
a high quality factor
the oscillator strength of the emitter. Therefore, in
order to achieve strong coupling experimentally, the cavity must have
a high quality factor ![]() (
(
![]() ) and a small
effective volume
) and a small
effective volume ![]() . The emitters must be placed close to the
anti-node of the electric field in the cavity, have transition
frequencies close to resonance with the cavity mode and exhibit high
oscillator strengths.
. The emitters must be placed close to the
anti-node of the electric field in the cavity, have transition
frequencies close to resonance with the cavity mode and exhibit high
oscillator strengths.
The linear model (discussed in Chapter 3) corresponds to
the coupling of two bosonic modes, ![]() and
and ![]() . The Hamiltonian
. The Hamiltonian ![]() can be straightforwardly diagonalized, giving:
can be straightforwardly diagonalized, giving:
with new Bose operators
These new modes are the polaritons (or dressed states) with
![\includegraphics[width=.5\linewidth]{chap2/Case-(c)-Pb_0.15--Splitting-with-det.eps}](img310.png) |
The energies defined by Eq. (2.56b) are
displayed in Fig. 2.1 with dashed lines, on
top of that of the bare modes, with thick lines, as detuning is varied
by changing the energy of the emitter and keeping that of the cavity
constant. The anticrossing always keeps the upper mode U
higher in energy than the lower L one, strongly admixing the light
and matter character of both particles. If the system is initially
prepared as a bare state--which is the natural picture when reaching
the SC from the excited state of an emitter--the dynamics is that of
an oscillatory transfer of energy between light and matter. In an
empty cavity, the time evolution of the probability to have an exciton
when there was one at ![]() , is given by:
, is given by:
which results in oscillations between the bare modes at the so-called Rabi frequency, given by
On the other hand, when the coupled modes are far from resonance
![]() , they affect perturbatively each other as we can see in
Fig. 2.1. In this regime, the small
difference in energy between the coupled and bare modes is known as
the Stark shift. The Rabi frequency, when
, they affect perturbatively each other as we can see in
Fig. 2.1. In this regime, the small
difference in energy between the coupled and bare modes is known as
the Stark shift. The Rabi frequency, when
![]() is
is
![]() so
that the Stark shift of each mode amounts to the same quantity
so
that the Stark shift of each mode amounts to the same quantity
The second interesting possibility is when the matter field is a
2LS. We will denote it by ![]() for clarity and discuss it in more
details in Chapters 5 and 6. The
Jaynes-Cummings Hamiltonian
for clarity and discuss it in more
details in Chapters 5 and 6. The
Jaynes-Cummings Hamiltonian
![]() can be
diagonalized in a given manifold with a fixed (and integer)
number of excitation
can be
diagonalized in a given manifold with a fixed (and integer)
number of excitation
![]() :
:
![]() . Rewriting the Hamiltonian
as a sum of all manifold's contributions,
. Rewriting the Hamiltonian
as a sum of all manifold's contributions,
it can be diagonalized in each subspace as
The eigenstates and eigenenergies are now
as well as the (half) Rabi frequency:
In the case of the Stark shifts, only that of the 2LS depends on the manifold:
The manifold structure is the fundamental difference between the
coupling of mode ![]() with a bosonic or a fermionic mode. The
with a bosonic or a fermionic mode. The
![]() -manifold in the first linear case, is composed by the
-manifold in the first linear case, is composed by the ![]() states
states
![]() with
with
![]() . The Hamiltonian can be also
written in these terms, in the bare or polariton basis,
. The Hamiltonian can be also
written in these terms, in the bare or polariton basis,
which makes it explicit that the energy of an excitation,
this indistinguishability is lost. The energy
All these cases are indistinguishable when the excitation is very low
and the system only probes up to the first manifold, as it is not
until a second excitation arrives that interactions or fermionic
effects enter the picture. It is one of the goals of this text to
explore the differences arising between the different models and
physical systems when ![]() .
.
A last interesting point to discuss is the coherent excitation of a
mode via coupling to a monochromatic laser. For instance, the cavity
field can be excited directly with a classical electromagnetic field
![]() (in a coherent state) with frequency
(in a coherent state) with frequency
![]() , like that of
Eq. (2.13). The corresponding Hamiltonian,
, like that of
Eq. (2.13). The corresponding Hamiltonian,
drives the cavity field into a coherent state. The same can happen with the excitonic field, changing
Elena del Valle ©2009-2010-2011-2012.


![$\displaystyle \frac{d\rho}{dt}=i[\rho,H]\,.$](img285.png)
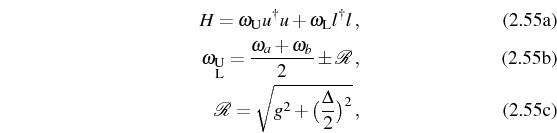
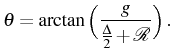
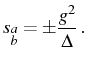
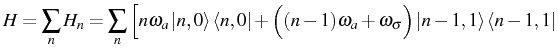
![$\displaystyle + g\sqrt{n} \Big( \ket{n-1,1}\bra{n,0}+ \ket{n,0}\bra{n-1,1} \Big)\Big]\,,$](img324.png)
![$\displaystyle H=\sum_n \Big[ \omega_\mathrm{U}^n\mid\mid 1_n,0\rangle\rangle \l...
..._\mathrm{L}^n\mid\mid 0,1_n\rangle\rangle \langle\langle 0,1_n\mid\mid \Big]\,.$](img325.png)
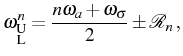
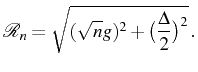
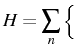
![$\displaystyle \Big[(n-m)\omega_a+m\omega_b\Big] \ket{n-m,m}\bra{n-m,m}+$](img334.png)
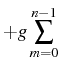
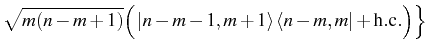
![$\displaystyle \Big[(n-p)\omega_\mathrm{U}+p\omega_\mathrm{L}\Big] \mid\mid n-p,p\rangle\rangle \langle\langle n-p,p\mid\mid \,,$](img339.png)